Kaggle競合数字認識分析

こんにちは、Habr！







約束どおり、私はMLClass.ruのメンバーと一緒に働いていた間に解決した問題の分析を公開し続けています。 今回は、例としてKaggleプラットフォームの数字Digit Recognizerを認識するというよく知られたタスクを使用して、主成分の方法を分析します。 この記事は、データ分析の勉強を始めたばかりの初心者に役立ちます。 ところで、 Applied Data Analysisコースに登録するのに遅すぎることはありません。この分野で可能な限り迅速に情報を収集する機会があります。

エントリー

この作業は、モデルサイズのサンプルサイズへの依存性を研究する研究の自然な継続です。 限られたコンピューティングリソースの条件で許容可能な結果を​​得るために、トレーニングサンプルで使用されるオブジェクトの数を減らす可能性を示しました。 ただし、オブジェクトの数に加えて、使用される機能の量もデータサイズに影響します。 同じデータでこの可能性を考慮してください。 使用されるデータは以前の研究で詳細に研究されたため、トレーニングサンプルをRにロードするだけです。

library(readr) library(caret) library(ggbiplot) library(ggplot2) library(dplyr) library(rgl) data_train <- read_csv("train.csv") ## |================================================================================| 100% 73 MB
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

既に知っているように、データには42,000個のオブジェクトと784個の特徴があり、これらは画像を構成する各ピクセルの輝度値です。 サンプルを60/40の比率でトレーニングとテストに分割します。

 set.seed(111) split <- createDataPartition(data_train$label, p = 0.6, list = FALSE) train <- slice(data_train, split) test <- slice(data_train, -split)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、定数値を持つ記号を削除します。

 zero_var_col <- nearZeroVar(train, saveMetrics = T) train <- train[, !zero_var_col$nzv] test <- test[, !zero_var_col$nzv] dim(train) ## [1] 25201 253
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

その結果、253個の兆候が残りました。

理論

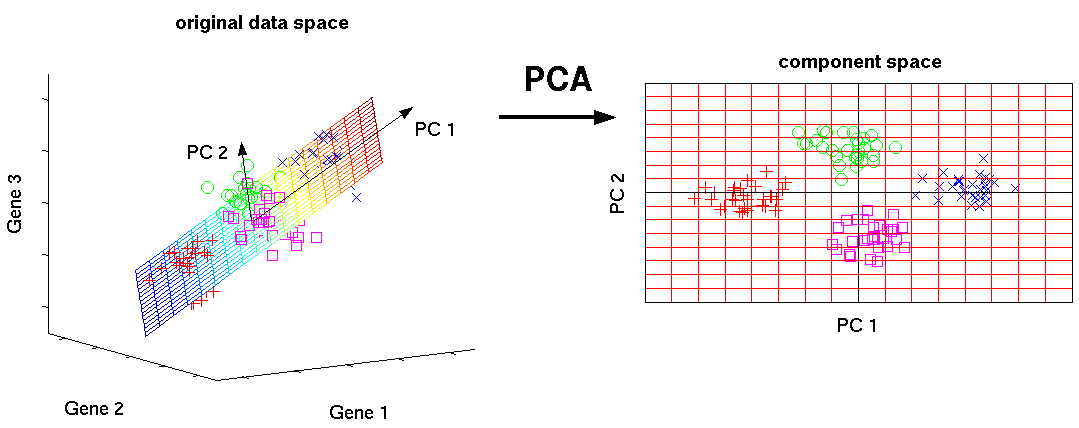
主成分分析（PCA）は、基本特性を新しい特性に変換します。各特性は、元の特性の線形結合であり、データの広がり（つまり、平均からの標準偏差）が最大になります。 このメソッドは、データを視覚化し、データの次元を減らす（圧縮）ために使用されます。

PCA

より明確にするために、トレーニングセットから1000個のオブジェクトをランダムに選択し、最初の2つの標識のスペースにそれらを描きます。

 train_1000 <- train[sample(nrow(train), size = 1000),] ggplot(data = train_1000, aes(x = pixel152, y = pixel153, color = factor(label))) + geom_point()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

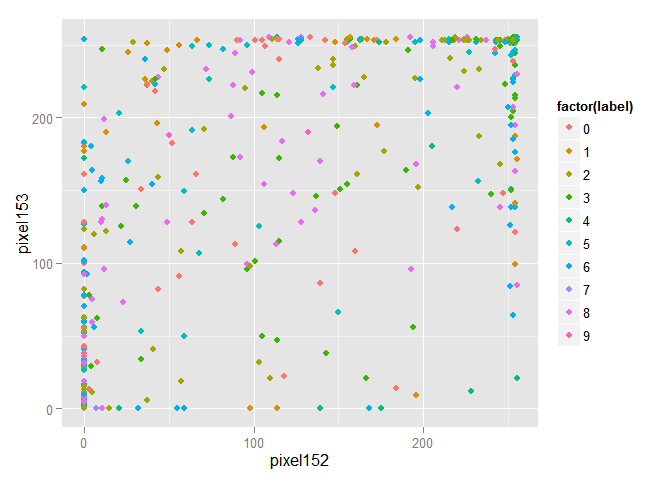
明らかに、オブジェクトは混在しており、1つのクラスに属するオブジェクトのグループを区別するのは問題です。 主成分法を使用してデータを変換し、最初の2つの成分の空間に描画します。 コンポーネントは、それらに沿って広がるデータの広がりに応じて降順で配置されることに注意してください。

 pc <- princomp(train_1000[, -1], cor=TRUE, scores=TRUE) ggbiplot(pc, obs.scale = 1, var.scale = 1, groups = factor(train_1000$label), ellipse = TRUE, circle = F, var.axes = F) + scale_color_discrete(name = '') + theme(legend.direction = 'horizontal', legend.position = 'top')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

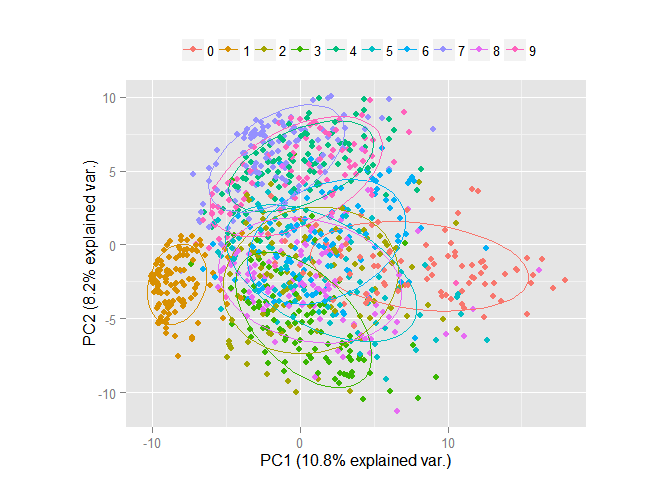
明らかに、たった2つの記号のスペースでさえ、オブジェクトの明示的なグループはすでに区別できます。 ここで、同じデータを考えますが、最初の3つのコンポーネントのスペースに既にあります。

 plot3d(pc$scores[,1:3], col= train_1000$label + 1, size = 0.7, type = "s")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

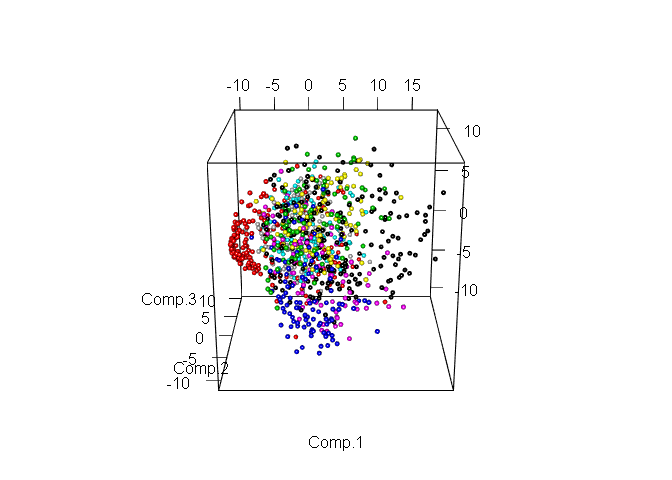
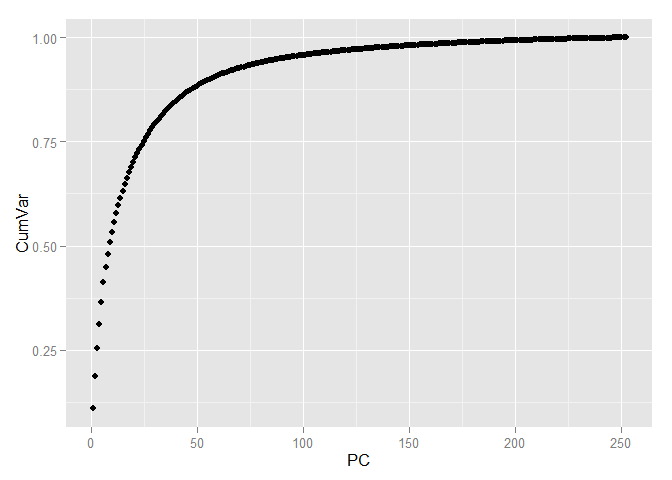
さまざまなクラスの割り当てがさらに簡素化されました。 次に、今後の作業に使用するコンポーネントの数を選択します。 これを行うために、分散の比率とそれを説明するコンポーネントの数を見てみましょうが、既にトレーニングサンプル全体を使用しています。

 pc <- princomp(train[, -1], cor=TRUE, scores=TRUE) variance <- pc$sdev^2/sum(pc$sdev^2) cumvar <- cumsum(variance) cumvar <- data.frame(PC = 1:252, CumVar = cumvar) ggplot(data = cumvar, aes(x = PC, y = CumVar)) + geom_point()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 variance <- data.frame(PC = 1:252, Var = variance*100) ggplot(data = variance[1:10,], aes(x = factor(PC), y = Var)) + geom_bar(stat = "identity")
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

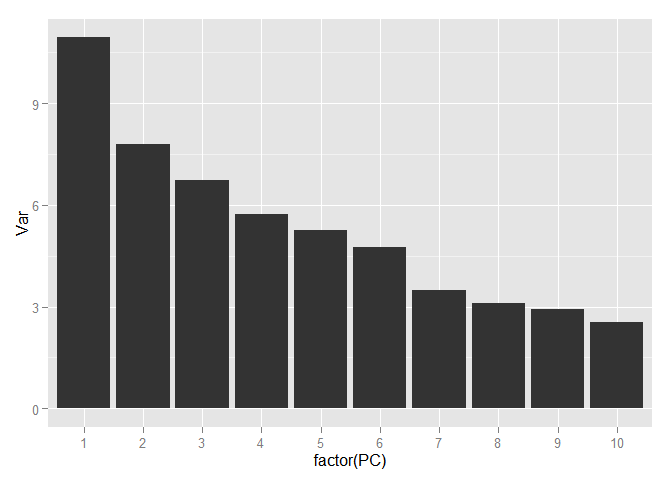
 sum(variance$Var[1:70]) ## [1] 92.69142
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

データに含まれる情報の90％以上を保存するには、70個のコンポーネントで十分です。 784の兆候から70に到達し、同時に、データ変動の10％未満を失いました！



トレーニングサンプルとテストサンプルを主要コンポーネントのスペースに変換します。

 train <- predict(pc) %>% cbind(train$label, .) %>% as.data.frame(.) %>% select(1:71) colnames(train)[1]<- "label" train$label <- as.factor(train$label) test %<>% predict(pc, .) %>% cbind(test$label, .) %>% as.data.frame(.) %>% select(1:71) colnames(test)[1]<- "label"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

モデルパラメーターを選択するには、最新のプロセッサのマルチコアテクノロジを使用して並列計算を実行する機能を提供するキャレットパッケージを使用します。

 library("doParallel") cl <- makePSOCKcluster(2) registerDoParallel(cl)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Knn

それでは、変換されたデータを使用して予測モデルの作成を始めましょう。 k最近傍（ KNN ）メソッドを使用して最初のモデルを作成します。 このモデルには、パラメータを1つだけ指定します-オブジェクトの分類に使用される近くのオブジェクトの数。 このパラメーターは、10分割サンプリングで10分割交差検定（CV ）を使用して選択します。 評価は、元のオブジェクトのランダムに選択された部分に対して行われます。 モデルの品質を評価するために、オブジェクトの正確に予測されたクラスの割合である精度メトリックを使用します。

 set.seed(111) train_1000 <- train[sample(nrow(train), size = 1000),] ctrl <- trainControl(method="repeatedcv",repeats = 3)       . knnFit <- train(label ~ ., data = train_1000, method = "knn", trControl = ctrl,tuneLength = 20) knnFit ## k-Nearest Neighbors ## ## 1000 samples ## 70 predictor ## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' ## ## No pre-processing ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 899, 901, 900, 901, 899, 899, ... ## Resampling results across tuning parameters: ## ## k Accuracy Kappa Accuracy SD Kappa SD ## 5 0.8749889 0.8608767 0.03637257 0.04047629 ## 7 0.8679743 0.8530101 0.03458659 0.03853048 ## 9 0.8652707 0.8500155 0.03336461 0.03713965 ## 11 0.8529954 0.8363199 0.03692823 0.04114777 ## 13 0.8433141 0.8255274 0.03184725 0.03548771 ## 15 0.8426833 0.8248052 0.04097424 0.04568565 ## 17 0.8423694 0.8244683 0.04070299 0.04540152 ## 19 0.8340150 0.8151256 0.04291349 0.04788273 ## 21 0.8263450 0.8065723 0.03914363 0.04369889 ## 23 0.8200042 0.7995067 0.03872017 0.04320466 ## 25 0.8156764 0.7946582 0.03825163 0.04269085 ## 27 0.8093227 0.7875839 0.04299301 0.04799252 ## 29 0.8010018 0.7783100 0.04252630 0.04747852 ## 31 0.8019849 0.7794036 0.04327120 0.04827493 ## 33 0.7963572 0.7731147 0.04418378 0.04930341 ## 35 0.7936906 0.7701616 0.04012802 0.04478789 ## 37 0.7889930 0.7649252 0.04163075 0.04644193 ## 39 0.7863463 0.7619669 0.03947693 0.04404655 ## 41 0.7829758 0.7582087 0.03482612 0.03889550 ## 43 0.7796388 0.7544879 0.03745359 0.04179976 ## ## Accuracy was used to select the optimal model using the largest value. ## The final value used for the model was k = 5.
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

それを減らして、正確な値を取得します。

 grid <- expand.grid(k=2:5) knnFit <- train(label ~ ., data = train_1000, method = "knn", trControl = ctrl, tuneGrid=grid) knnFit ## k-Nearest Neighbors ## ## 1000 samples ## 70 predictor ## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' ## ## No pre-processing ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 900, 901, 901, 899, 901, 899, ... ## Resampling results across tuning parameters: ## ## k Accuracy Kappa Accuracy SD Kappa SD ## 2 0.8699952 0.8553199 0.03055544 0.03402108 ## 3 0.8799832 0.8664399 0.02768544 0.03082014 ## 4 0.8736591 0.8593777 0.02591618 0.02888557 ## 5 0.8726753 0.8582703 0.02414173 0.02689738 ## ## Accuracy was used to select the optimal model using the largest value. ## The final value used for the model was k = 3.
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

パラメーターkの値が3に等しい場合、モデルに最適なインジケーターがあります。この値を使用して、テストデータの予測を取得します。 混同表を作成し、 精度を計算します。

 library(class) prediction_knn <- knn(train, test, train$label, k=3) table(test$label, prediction_knn) ## prediction_knn ## 0 1 2 3 4 5 6 7 8 9 ## 0 1643 0 6 1 0 1 2 0 0 0 ## 1 0 1861 4 1 2 0 0 0 0 0 ## 2 7 7 1647 3 0 0 1 11 0 0 ## 3 1 0 9 1708 2 19 4 6 1 3 ## 4 0 4 0 0 1589 0 10 7 0 6 ## 5 3 2 1 20 1 1474 13 0 6 2 ## 6 0 0 0 1 2 3 1660 0 0 0 ## 7 0 6 3 0 2 0 0 1721 0 13 ## 8 0 1 0 11 1 16 12 4 1522 20 ## 9 0 0 1 3 3 5 1 23 5 1672 sum(diag(table(test$label, prediction_knn)))/nrow(test) ## [1] 0.9820227
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ランダムフォレスト

2番目のモデルはRandom Forestです。 このモデルでは、 mtryパラメーター（アンサンブルで使用される各ツリーを受信するときに使用される属性の数）を選択します。 このパラメーターに最適な値を選択するには、以前と同じ方法で行こう。

 rfFit <- train(label ~ ., data = train_1000, method = "rf", trControl = ctrl,tuneLength = 3) rfFit ## Random Forest ## ## 1000 samples ## 70 predictor ## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' ## ## No pre-processing ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 901, 900, 900, 899, 902, 899, ... ## Resampling results across tuning parameters: ## ## mtry Accuracy Kappa Accuracy SD Kappa SD ## 2 0.8526986 0.8358081 0.02889351 0.03226317 ## 36 0.8324051 0.8133909 0.03442843 0.03836844 ## 70 0.8026823 0.7802912 0.03696172 0.04118363 ## ## Accuracy was used to select the optimal model using the largest value. ## The final value used for the model was mtry = 2. grid <- expand.grid(mtry=2:6) rfFit <- train(label ~ ., data = train_1000, method = "rf", trControl = ctrl,tuneGrid=grid) rfFit ## Random Forest ## ## 1000 samples ## 70 predictor ## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' ## ## No pre-processing ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 898, 900, 900, 901, 900, 898, ... ## Resampling results across tuning parameters: ## ## mtry Accuracy Kappa Accuracy SD Kappa SD ## 2 0.8553016 0.8387134 0.03556811 0.03967709 ## 3 0.8615798 0.8457973 0.03102887 0.03458732 ## 4 0.8669329 0.8517297 0.03306870 0.03690844 ## 5 0.8739532 0.8595897 0.02957395 0.03296439 ## 6 0.8696883 0.8548470 0.03203166 0.03568138 ## ## Accuracy was used to select the optimal model using the largest value. ## The final value used for the model was mtry = 5.
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

4に等しいmtryを選択し、テストデータの精度を取得します。 利用可能なトレーニングデータからモデルを部分的にトレーニングしなければならなかったことに注意してください。 すべてのデータを使用するには、より多くのRAMが必要です。 ただし、前の作業で示したように、これは最終結果に大きな影響を与えません。

 library(randomForest) rfFit <- randomForest(label ~ ., data = train[sample(nrow(train), size = 15000),], mtry = 4) prediction_rf<-predict(rfFit,test) table(test$label, prediction_rf) ## prediction_rf ## 0 1 2 3 4 5 6 7 8 9 ## 0 1608 0 6 3 4 1 20 2 9 0 ## 1 0 1828 9 9 3 5 3 2 9 0 ## 2 12 9 1562 16 15 5 6 19 31 1 ## 3 12 1 26 1625 2 33 12 14 22 6 ## 4 0 6 11 1 1524 0 22 7 6 39 ## 5 12 3 3 48 12 1415 10 1 15 3 ## 6 13 4 8 0 4 11 1623 0 3 0 ## 7 3 14 25 2 13 3 0 1653 4 28 ## 8 4 10 12 64 8 21 12 5 1428 23 ## 9 4 4 10 39 38 10 0 39 7 1562 sum(diag(table(test$label, prediction_rf)))/nrow(test) ## [1] 0.9421989
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

SVM

そして最後に、 サポートベクターマシン 。 このモデルでは、 ラジアルカーネルが使用され、シグマ（正規化パラメーター）とC （カーネルの形状を決定するパラメーター）の2つのパラメーターが選択されます。

 svmFit <- train(label ~ ., data = train_1000, method = "svmRadial", trControl = ctrl,tuneLength = 5) svmFit ## Support Vector Machines with Radial Basis Function Kernel ## ## 1000 samples ## 70 predictor ## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' ## ## No pre-processing ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 901, 900, 898, 900, 900, 901, ... ## Resampling results across tuning parameters: ## ## C Accuracy Kappa Accuracy SD Kappa SD ## 0.25 0.7862419 0.7612933 0.02209354 0.02469667 ## 0.50 0.8545924 0.8381166 0.02931921 0.03262332 ## 1.00 0.8826064 0.8694079 0.02903226 0.03225475 ## 2.00 0.8929180 0.8808766 0.02781461 0.03090255 ## 4.00 0.8986322 0.8872208 0.02607149 0.02898200 ## ## Tuning parameter 'sigma' was held constant at a value of 0.007650572 ## Accuracy was used to select the optimal model using the largest value. ## The final values used for the model were sigma = 0.007650572 and C = 4. grid <- expand.grid(C = 4:6, sigma = seq(0.006, 0.009, 0.001)) svmFit <- train(label ~ ., data = train_1000, method = "svmRadial", trControl = ctrl,tuneGrid=grid) svmFit ## Support Vector Machines with Radial Basis Function Kernel ## ## 1000 samples ## 70 predictor ## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' ## ## No pre-processing ## Resampling: Cross-Validated (10 fold, repeated 3 times) ## Summary of sample sizes: 901, 900, 900, 899, 901, 901, ... ## Resampling results across tuning parameters: ## ## C sigma Accuracy Kappa Accuracy SD Kappa SD ## 4 0.006 0.8943835 0.8824894 0.02999785 0.03335171 ## 4 0.007 0.8970537 0.8854531 0.02873482 0.03194698 ## 4 0.008 0.8984139 0.8869749 0.03068411 0.03410783 ## 4 0.009 0.8990838 0.8877269 0.03122154 0.03469947 ## 5 0.006 0.8960834 0.8843721 0.03061547 0.03404636 ## 5 0.007 0.8960703 0.8843617 0.03069610 0.03412880 ## 5 0.008 0.8990774 0.8877134 0.03083329 0.03427321 ## 5 0.009 0.8990838 0.8877271 0.03122154 0.03469983 ## 6 0.006 0.8957534 0.8840045 0.03094360 0.03441242 ## 6 0.007 0.8963971 0.8847267 0.03081294 0.03425451 ## 6 0.008 0.8990774 0.8877134 0.03083329 0.03427321 ## 6 0.009 0.8990838 0.8877271 0.03122154 0.03469983 ## ## Accuracy was used to select the optimal model using the largest value. ## The final values used for the model were sigma = 0.009 and C = 4. library(kernlab) svmFit <- ksvm(label ~ ., data = train,type="C-svc",kernel="rbfdot",kpar=list(sigma=0.008),C=4) prediction_svm <- predict(svmFit, newdata = test) table(test$label, prediction_svm) ## prediction_svm ## 0 1 2 3 4 5 6 7 8 9 ## 0 1625 0 5 1 0 3 13 0 6 0 ## 1 1 1841 6 6 4 1 0 3 5 1 ## 2 8 4 1624 5 7 1 1 13 11 2 ## 3 2 0 18 1684 0 23 2 6 12 6 ## 4 1 3 3 0 1567 0 9 7 5 21 ## 5 8 3 2 24 6 1465 7 0 6 1 ## 6 2 1 2 1 5 5 1649 0 1 0 ## 7 3 8 15 3 3 0 0 1695 3 15 ## 8 1 6 10 10 5 9 3 4 1530 9 ## 9 3 1 5 13 14 9 0 21 3 1644 sum(diag(table(test$label, prediction_svm)))/nrow(test) ## [1] 0.9717245
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

モデルのアンサンブル

先ほど作成した3つのモデルの集合である4番目のモデルを作成しましょう。 このモデルは、使用されるモデルのほとんどが「投票」である値を予測します。

 all_prediction <- cbind(as.numeric(levels(prediction_knn))[prediction_knn], as.numeric(levels(prediction_rf))[prediction_rf], as.numeric(levels(prediction_svm))[prediction_svm]) predictions_ensemble <- apply(all_prediction, 1, function(row) { row %>% table(.) %>% which.max(.) %>% names(.) %>% as.numeric(.) }) table(test$label, predictions_ensemble) ## predictions_ensemble ## 0 1 2 3 4 5 6 7 8 9 ## 0 1636 0 5 1 0 1 8 0 2 0 ## 1 1 1851 3 5 3 0 0 1 4 0 ## 2 7 6 1636 3 6 0 0 11 7 0 ## 3 6 0 14 1690 1 18 4 8 7 5 ## 4 0 5 4 0 1573 0 12 6 2 14 ## 5 5 1 2 21 5 1478 7 0 3 0 ## 6 3 1 2 0 5 3 1651 0 1 0 ## 7 1 11 12 2 1 0 0 1704 0 14 ## 8 1 5 11 17 4 13 4 3 1514 15 ## 9 4 2 4 21 11 5 0 20 1 1645 sum(diag(table(test$label, predictions_ensemble)))/nrow(test) ## [1] 0.974939
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

まとめ

テストサンプルで次の結果が得られました。

モデル	試験精度
Knn	0.981
ランダムフォレスト	0.948
SVM	0.971
アンサンブル	0.974

最高の精度インジケータには、k最近傍（ KNN ）メソッドを使用したモデルがあります。



Kaggle Webサイトのモデルの評価を次の表に示します。

モデル	Kaggleの精度
Knn	0.97171
ランダムフォレスト	0.93286
SVM	0.97786
アンサンブル	0.97471

ここでSVMが最良の結果をもたらします。

固有顔

そして最後に、すでに好奇心から、主成分のメソッドによって生成される変換を見てみましょう。 このために、まず、元の形式で数字の画像を取得します。

 set.seed(100) train_1000 <- data_train[sample(nrow(data_train), size = 1000),] colors<-c('white','black') cus_col<-colorRampPalette(colors=colors) default_par <- par() number_row <- 28 number_col <- 28 par(mfrow=c(5,5),pty='s',mar=c(1,1,1,1),xaxt='n',yaxt='n') for(i in 1:25) { z<-array(as.matrix(train_1000)[i,-1],dim=c(number_row,number_col)) z<-z[,number_col:1] image(1:number_row,1:number_col,z,main=train_1000[i,1],col=cus_col(256)) } par(default_par)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、同じ数字の画像ですが、すでにPCAメソッドを使用して最初の70個のコンポーネントを残した後です。 結果のオブジェクトは、固有面と呼ばれます

 zero_var_col <- nearZeroVar(train_1000, saveMetrics = T) train_1000_cut <- train_1000[, !zero_var_col$nzv] pca <- prcomp(train_1000_cut[, -1], center = TRUE, scale = TRUE) restr <- pca$x[,1:70] %*% t(pca$rotation[,1:70]) restr <- scale(restr, center = FALSE , scale=1/pca$scale) restr <- scale(restr, center = -1 * pca$center, scale=FALSE) restr <- as.data.frame(cbind(train_1000_cut$label, restr)) test <- data.frame(matrix(NA, nrow = 1000, ncol = ncol(train_1000))) zero_col_number <- 1 for (i in 1:ncol(train_1000)) { if (zero_var_col$nzv[i] == F) { test[, i] <- restr[, zero_col_number] zero_col_number <- zero_col_number + 1 } else test[, i] <- train_1000[, i] } par(mfrow=c(5,5),pty='s',mar=c(1,1,1,1),xaxt='n',yaxt='n') for(i in 1:25) { z<-array(as.matrix(test)[i,-1],dim=c(number_row,number_col)) z<-z[,number_col:1] image(1:number_row,1:number_col,z,main=test[i,1],col=cus_col(256)) } par(default_par)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次回はテキストマイニングのタスクの1つを検討しますが、今のところは実用データ分析のコースに参加できます-お勧めです！