少しの材料
この場合、点P 1 ... P nの形式でテーブルを設定する関数の中間値の復元は、補間と呼ばれます。 補間する方法は多数ありますが、それらのすべてを、対応するセグメントの中間点を計算するためのn -1関数を見つける必要があるという事実にまで減らすことができます。 さらに、与えられたポイントは、対応する関数を通じて必然的に計算可能でなければなりません。 これに基づいて、グラフを作成できます。

関数f iは大きく異なりますが、ほとんどの場合、ある程度の多項式を使用します。 この場合、結果の補間関数(点P iで区切られた区間で区分的に定義される)は、 スプラインと呼ばれます。
さまざまなグラフ作成ツール(エディターとライブラリー)では、「美しい補間」問題の解決方法が異なります。 記事の最後に、既存のオプションの簡単な概要があります。 なぜ最後に? そのため、一連の計算と反射が与えられた後、どの「深刻な人」がどのメソッドを使用するかを推測できます。
実験を入れます
最も単純な例は線形補間で、最初の次数の多項式が使用され、その結果、指定された点を結ぶ破線が得られます。
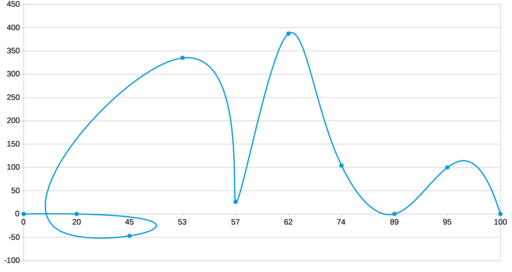
いくつかの詳細を追加しましょう。 ここにポイントのセットがあります( ほとんど天井から取られています):
0 0 20 0 45 -47 53 335 57 26 62 387 74 104 89 0 95 100 100 0
これらのポイントの線形補間の結果は次のようになります。
ただし、上記のように、最終的に滑らかな曲線を得たい場合があります。
滑らかさとは何ですか? 家庭の答え:鋭い角はありません。 数学:導関数の連続性。 さらに、数学では、滑らかさは最後の連続微分の数とこの連続性が維持される領域に等しい次数を持ちます。 つまり、関数がセグメント上で次数1の滑らかさを持っている場合[ a ; b ]、これは[ a ; b ]それは連続的な一階微分を持っていますが、二階微分は既にいくつかの点で壊れています。
滑らかさの文脈では、スプラインには欠陥の概念があります。 スプライン欠陥は、その程度と滑らかさの違いです。 スプライン次数は、そこで使用される多項式の最大次数です。
スプラインの「危険な」点(滑らかさが損なわれる可能性がある)は正確にP i 、つまり、ある多項式から別の多項式への遷移が発生するセグメントの接合点であることに注意することが重要です。 他のすべてのポイントは「安全」です。その定義の領域の多項式は微分の連続性に問題がないためです。
滑らかな補間を実現するには、多項式の次数を増やし、係数を選択して、微分の連続性が境界点で維持されるようにする必要があります。
従来、このような問題を解決し、1次および2次導関数の連続性を実現するために、3次の多項式が使用されていました。 起こることは、欠陥1の3次スプラインと呼ばれます。 データの外観は次のとおりです。

曲線は本当に滑らかです。 しかし、これが関心のある人に示す必要のあるプロセスまたは現象のグラフであると仮定する場合、この方法はおそらく適切ではありません。 問題は偽の極値です。 それらは、補間関数の滑らかさを確保するために設計された曲率が大きすぎるために現れました。 しかし、視聴者は関数のピーク値に関してだまされることが判明したため、そのような動作はまったく必要ありません。 実際、これらの値を視覚化するために、すべてが開始されました。
そのため、他のソリューションを探す必要があります。
欠陥1の3次スプラインとは別の従来の解決策は、ラグランジュ多項式です。 これらは、与えられたポイントで与えられた値をとる次数n -1の多項式です。 つまり、セグメンテーションはここでは発生せず、シーケンス全体が1つの多項式で記述されます。
しかし、結果は次のとおりです。
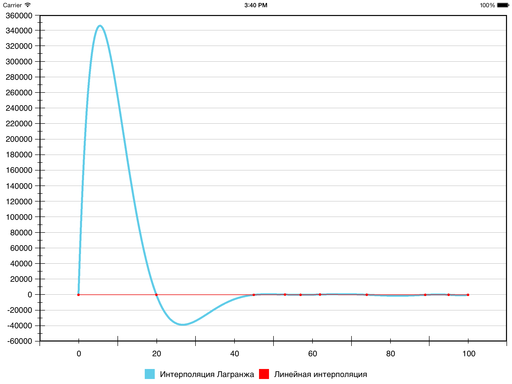
もちろん、滑らかさはありますが、視認性が非常に低下しているため、他の方法を探す価値があるかもしれません。 一部のデータセットでは、結果は正常ですが、一般的な場合、線形補間に関する誤差(したがって、偽の極値)は大きすぎることがあります-すべてのセグメントに多項式が1つしかないためです。
コンピュータグラフィックスでは、 k番目の多項式で表されるベジェ曲線が非常に広く使用されています。
構築に関与するk + 1ポイントから、最終曲線は最初と最後のみを通過するため、補間されません。 残りのk -1ポイントは、曲線を引き付ける一種の「重心」の役割を果たします。
3次ベジェ曲線の例を次に示します。

これを補間にどのように使用できますか? これらの曲線に基づいて、スプラインを作成することもできます。 つまり、スプラインの各セグメントには、 k次の独自のベジェ曲線があります(ところで、 k = 1は線形補間を提供します)。 そして、唯一の問題は、 kの値とk -1個の中間点を見つける方法です。
無限に多くのオプションがあります( kは何によっても制限されないため)が、古典的なオプションを検討します: k = 3。
最終曲線が滑らかになるためには、合成スプラインの欠陥1を達成する必要があります。つまり、3次スプラインの古典的なバージョンで行われるように、セグメント( P i )の接合点で1次および2次導関数の連続性を維持する必要があります。
この問題の解決策については、(ソースコードを使用して)詳細に説明します 。
テストスイートで行われる処理は次のとおりです。

それは良くなりました:まだ偽の極値がありますが、少なくともそれらは実際のものとそれほど違いはありません。
考えて実験する
平滑化条件を弱めようとすることができます。1ではなく欠陥2が必要です。つまり、1次導関数の連続性のみを維持します。
欠陥2を達成するための十分な条件は、補間されたシーケンスの特定の点に隣接する3次ベジェ曲線の中間制御点が、同じ線上で同じ距離にあるこの線上にあることです。

点C i -1 (2) 、 P iおよびC i (1)が存在する線として、点P iでの補間関数のグラフへの接線をとることが望ましい。 これにより、ベジェ曲線はその制御点上に構築された破線で区切られているため、誤った極値がなくなります(この破線に自己交差がない場合)。
試行錯誤により、補間されたシーケンスのポイントから中間コントロールまでの距離を計算するためのヒューリスティックは次のとおりです。
ヒューリスティック1 

最初と最後の中間制御点は、それぞれグラフの最初と最後の点に等しくなります(点C 1 (1)とC n -1 (2)は、それぞれ点P 1とP nと一致します)。
この場合、次の曲線が得られます。

どうやら、偽の極値はもうありません。 ただし、線形補間と比較すると、場所によっては誤差が非常に大きくなります。 さらに小さくすることもできますが、ここではさらにトリッキーなヒューリスティックが使用されます。
現在のオプションに到達し、滑らかさを1桁減らしました。 スプラインに3の欠陥を持たせることができます。実際、正式にそうすることにより、関数はまったくスムーズになりません。1次導関数でさえブレークを受ける可能性があります。 しかし、慎重に引き裂くと、視覚的に何も悪いことは起こりません。
点P iから点C i -1 (2)およびC i (1)までの距離が等しいという要件を放棄しますが、同時にそれらをすべて同じ線上に保ちます。
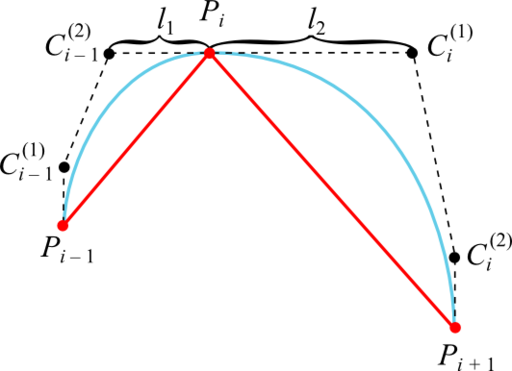
距離を計算するためのヒューリスティックは次のようになります。
ヒューリスティック2
l 1とl 2の計算は、「ヒューリスティック1」と同じです。
ただし、この場合、ポイントP iとP i + 1が縦座標で一致するかどうかを確認する価値があります。一致する場合は、 l 1 = l 2 = 0に設定します。真実のデータ表示の観点から重要です)。
ただし、この場合、ポイントP iとP i + 1が縦座標で一致するかどうかを確認する価値があります。一致する場合は、 l 1 = l 2 = 0に設定します。真実のデータ表示の観点から重要です)。
結果は次のとおりです。
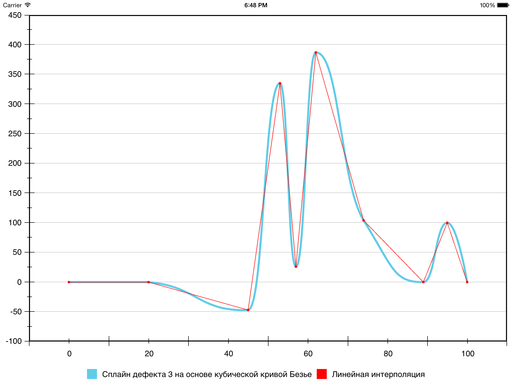
その結果、6番目のセグメントでエラーが減少し、7番目のセグメントでエラーが増加しました。ベジエの曲率は、予想よりも大きいことが判明しました。 曲率を強制的に減少させ、それによってベジエをセグメントの境界点を接続するラインセグメントの近くに「押し付ける」ことにより、状況を修正できます。 これには、次のヒューリスティックが使用されます。
ヒューリスティック3
点P i ( x i 、 y i )およびP i + 1 ( x i + 1 、 y i + 1 )での接線の交点の横座標がセグメント[ x i ; x i + 1 ]、 l 1またはl 2をゼロに設定します。 点P iの接線が上向きの場合、 l 1とl 2の最大値はゼロであり、下の場合は最小値であると想定します。
結果は次のとおりです。
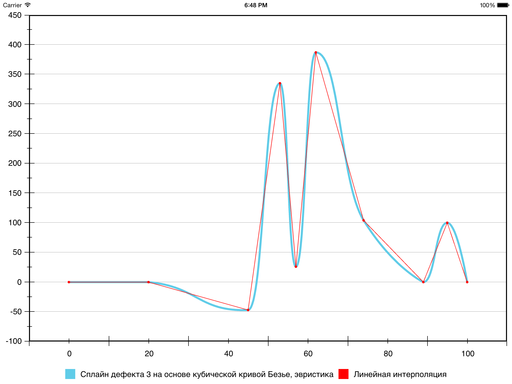
これで、達成された目標を認識することが決定されました。
たぶん誰かがコードを必要としています 。
そして、どのように人々はそれをしますか?
約束されたレビュー。 もちろん、問題を解決する前に、誰が何を自慢できるかを見ました。そして、それから私たちはそれを自分自身で、可能であればより良くする方法を見つけ始めました。 しかし、彼らがそれをするやいなや、彼らが再び利用可能なツールを調べ、その結果を私たちの実験の成果と比較したことは喜びではなかった。 行きましょう。
MS Excel

これは、ベジェ曲線に基づいて、上記で説明した欠陥1のスプラインに非常に似ています。 確かに、その最も純粋な形式とは異なり、偽極値は2つしかありません-最初と2番目のセグメント(4つありました)。 どうやら、中間制御点の古典的な検索に他のヒューリスティックが追加されたようです。 しかし、彼らはすべての誤った極端から救いませんでした。
Libreoffice Calc
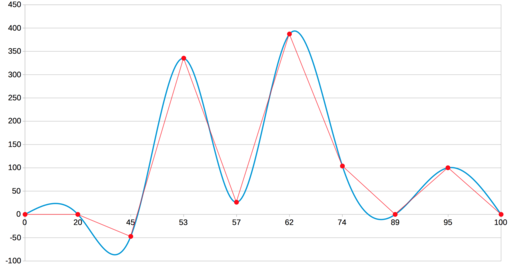
設定では、これは3次スプラインと呼ばれます。 明らかに、それはベジエにも基づいており、ここに結果の正確なコピーがあります。4つの偽の極値がすべて揃っています。
ここでは考慮していない別のタイプの補間があります:Bスプライン。 しかし、私たちのタスクには、このような結果が得られるため、明らかに適切ではありません:)

Highcharts 、最も人気のあるチャート作成JSライブラリの1つ

ここでは、補間されたシーケンスのポイントから中間コントロールのポイントまでの距離が等しい場合の「接線法」を示します。 偽の極値はありませんが、線形補間(7番目のセグメント)に関して比較的大きな誤差があります。
別の人気のあるJSライブラリamCharts

この写真はエクセルに非常によく似ており、同じ場所で同じ2つの極端な極端です。
Coreplot 、iOSおよびOS X用の最も人気のあるチャートライブラリ

偽の極値があり、欠陥1のベジェベースのスプラインが使用されていることがわかります。
ライブラリは開いているので、コードを調べて自分で確認できます。
aChartEngine 、Androidで最も人気のあるチャート作成ライブラリのようなもの

次数n -1のベジェ曲線に最も似ていますが、ライブラリ自体ではグラフは「キュービックライン」と呼ばれます。 変だ! 間違った極値があるだけでなく、原則として補間条件が満たされていません。
結論の代わりに
最終的に、Highchartsが問題を最もよく解決したのは「大物」であることが判明しました。 ただし、この記事で説明する方法では、線形補間に関するエラーがさらに小さくなります。
一般的に、私はチャートエンジンのバグとして「鋭いコーナー」を報告してくれたバイヤーの要請でこれをしなければなりませんでした。 説明された経験が誰かに役立つなら、私たちは喜んでいるでしょう。