
もちろん、データ構造の神聖な知識がなくても成功するプログラマーになることはできますが、一部のアプリケーションでは絶対に不可欠です。 たとえば、地図上の2点間の最短経路を計算する必要がある場合や、100万件のエントリを含む電話帳で名前を見つける場合などです。 データ構造がスポーツプログラミングで常に使用されているという事実は言うまでもありません。 それらのいくつかをより詳細に検討しましょう。
キュー
ルピに挨拶してください!

ルピは家族とホッケーをするのが大好きです。 「ゲーム」とは、次のことを意味します。

亀がゲートに飛び込むと、彼らは山の頂上に投げられます。 スタックに追加された最初の亀が最初にそれを残すことに注意してください。 これはQueueと呼ばれます。 日常生活で見られるキューのように、リストに最初に追加されたアイテムが最初にリストから離れます。 この構造は、 FIFO ( 先入れ先出し )とも呼ばれます。
挿入および削除操作はどうですか?
q = [] def insert(elem): q.append(elem) # print q def delete(): q.pop(0) # print q
スタック
このような楽しいホッケーゲームの後、ルピは皆のためにパンケーキを作ります。 彼女はそれらを1つの山に入れます。

すべてのパンケーキが準備できたら、ルピは家族全員に1つずつ提供します。

彼女が作った最初のパンケーキが最後に出されることに注意してください。 これはStackと呼ばれます。 リストに最後に追加されたアイテムが最初に残ります。 このデータ構造は、 LIFO (Last In First Out)とも呼ばれます。
アイテムを追加および削除しますか?
s = [] def push(elem): # - s.append(elem) print s def customPop(): # - s.pop(len(s)-1) print s
束
密度の塔を見たことがありますか?
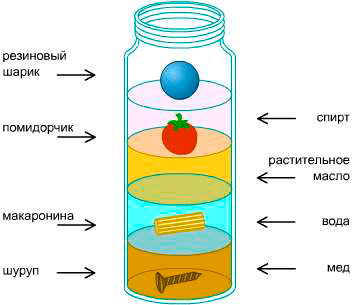
すべての要素は、密度に応じて、上から下に配置されます。 新しいオブジェクトを内部にドロップするとどうなりますか?

その密度に応じて、場所を取ります。
これがヒープの仕組みです。
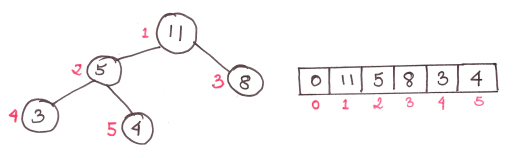
ヒープはバイナリツリーです。 これは、各親に2つの子があることを意味します。 そして、このデータ構造をヒープと呼びますが、通常の配列で表現されます。
また、ヒープの高さは常にlognです。nは要素の数です
この図は、次のルールに基づいたタイプmax-heapのヒープを示しています。子は親よりも小さい 。 子が常に親よりも大きい最小ヒープヒープもあります。
ヒープを操作するためのいくつかの簡単な関数:
global heap global currSize def parent(i): # i- return i/2 def left(i): # i- return 2*i def right(i): # i- return (2*i + 1)
既存のヒープにアイテムを追加する
まず、ヒープの一番下に要素を追加します。 配列の最後まで。 次に、適切な位置に収まるまで親要素と交換します。

アルゴリズム:
- ヒープの一番下にアイテムを追加します。
- 追加したアイテムを親と比較します。 順序が正しい場合、停止します。
- そうでない場合は、要素を交換して前の項目に戻ります。
コード:
def swap(a, b): # a b temp = heap[a] heap[a] = heap[b] heap[b] = temp def insert(elem): global currSize index = len(heap) heap.append(elem) currSize += 1 par = parent(index) flag = 0 while flag != 1: if index == 1: # flag = 1 elif heap[par] > elem: # - flag = 1 else: # swap(par, index) index = par par = parent(index) print heap
whileループの最大パス数はツリーの高さ、またはlognに等しいため、アルゴリズムの複雑さはO(logn)です。
最大ヒープ要素の取得
ヒープ内の最初の要素は常に最大であるため、(以前に記憶していた)削除して、最も低い要素に置き換えるだけです。 次に、関数を使用してヒープを正しい順序で配置します。
maxHeapify().

アルゴリズム:
- ルート要素を最下位のものに置き換えます。
- 新しいルートを子と比較します。 それらが正しい順序にある場合-停止します。
- そうでない場合は、ルート要素を子要素のいずれか(min-heapでは小さく、max-heapでは大きく)に置き換えて、手順2を繰り返します。
コード:
def extractMax(): global currSize if currSize != 0: maxElem = heap[1] heap[1] = heap[currSize] # - heap.pop(currSize) # currSize -= 1 # maxHeapify(1) return maxElem def maxHeapify(index): global currSize lar = index l = left(index) r = right(index) #, ; - if l <= currSize and heap[l] > heap[lar]: lar = l if r <= currSize and heap[r] > heap[lar]: lar = r if lar != index: swap(index, lar) maxHeapify(lar)
繰り返しますが、maxHeapify関数の呼び出しの最大数は、ツリーの高さ、またはlognに等しく、これはアルゴリズムの複雑さがO(logn)であることを意味します。
ランダム配列の束を作ります
さて、これを行うには2つの方法があります。 1つは、各要素を1つずつヒープに挿入することです。 シンプルですが、完全に非効率的です。 この場合のアルゴリズムの複雑さはO(nlogn)になります。 O(logn)関数はn回実行されます。
より効率的な方法は、(サブサイズ)に対して(currSize / 2)から最初の要素までmaxHeapify関数を使用することです。
複雑さはO(n)であり、残念ながらこの声明の証拠はこの記事の範囲外です。 currSize / 2からcurrSizeまでのヒープ部分の要素には子孫がなく、そのように作成されたサブヒープのほとんどは高さがlognより小さいことを理解してください。
コード:
def buildHeap(): global currSize for i in range(currSize/2, 0, -1): # range() - , . print heap maxHeapify(i) currSize = len(heap)-1

実際、なぜこれだけなのでしょうか?
ヒープは、奇妙なことに「 ヒープソート 」と呼ばれる特別なタイプのソートを実装するために必要です。 O(n 2 )のひどい複雑さを持つ、効率の低い「挿入ソート」や「バブルソート」とは異なり、「ヒープソート」はO(nlogn)の複雑さを持ちます。
わいせつな実装は簡単です。 ヒープから最大(ルート)要素を順番に抽出し続け、ヒープが空になるまで配列に書き込みます。
コード:
def heapSort(): for i in range(1, len(heap)): print heap heap.insert(len(heap)-i, extractMax()) # currSize = len(heap)-1
上記のすべてを要約するために、私は束を扱うための関数を含む数行のコードを書き、OOPファンのためにすべてをクラスの形式で設計しました。
簡単ですね。 そして、ここに祝うルピがあります!

ハッシュ
ルピは子供たちに形と色を区別するように教えたいと思っています。 これを行うために、彼女は膨大な数のマルチカラーのフィギュアを持ち帰りました。
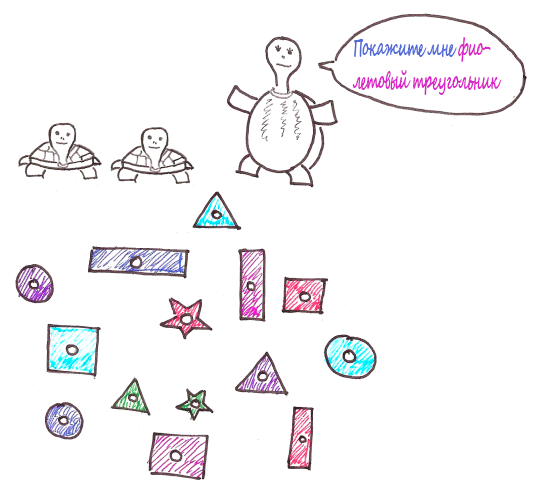
しばらくして、カメはついに混乱しました

そこで彼女は、プロセスを少し単純化するために別のおもちゃを取り出しました。
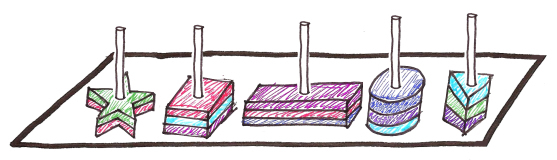
カメはすでに数字が形で分類されていることを知っていたので、それははるかに簡単になりました。 しかし、各投稿にマークを付けるとどうなりますか?

カメは今、特定の数字でポールをチェックし、はるかに少ない数字から選択する必要があります。 しかし、形状と色の組み合わせごとに個別の柱がある場合はどうでしょうか?
列番号が次のように計算されるとします。
フィオサマートレスクエア
f + u + o + t + p + e = 22 + 10 + 16 + 20 + 18 + 6 =柱92
赤い長方形
k + p + a + n + p + i = 12 + 18 + 1 + 17 + 18 + 33 =柱99
など
6 * 33 = 198通りの組み合わせが可能であることを知っているので、198本の柱が必要です。
列番号を計算するためのこの式をハッシュ関数と呼びます 。
コード:
def hashFunc(piece): words = piece.split(" ") # colour = words[0] shape = words[1] poleNum = 0 for i in range(0, 3): poleNum += ord(colour[i]) - 96 poleNum += ord(shape[i]) - 96 return poleNum
( キリル文字はもう少し複雑ですが、簡単にするために残しました。- 約per。 )
ここで、ピンク色の正方形がどこに保存されているかを調べる必要がある場合、次のように計算できます。
hashFunc(' ')
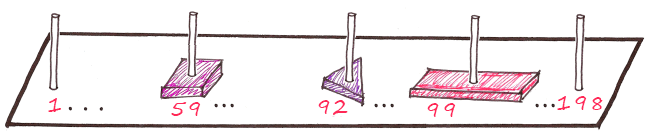
これは、ハッシュ関数によって要素の場所が決定されるハッシュテーブルの例です。
このアプローチでは、要素の検索にかかる時間は要素の数に依存しません。 O(1)。 つまり、ハッシュテーブルでの検索時間は定数値です。
わかりましたが、「カーメルの四角形」を探しているとしましょう(もちろん、「キャラメル」という色が存在しない限り)。
hashFunc(' ')
99が返されます。これは、赤い長方形の番号と同じです。 これは「 衝突 」と呼ばれます。 競合を解決するために、「 連鎖方法 」を使用します。これは、各列に必要なレコードを検索するリストが格納されることを意味します。
したがって、キャラメルの長方形を赤に配置し、ハッシュ関数がこの列を指すときにそれらの1つを選択します。
適切なハッシュテーブルの鍵は、適切なハッシュ関数を選択することです。 間違いなく、これはハッシュテーブルを作成する上で最も重要なことであり、人々は高品質のハッシュ関数の開発に膨大な時間を費やしています。
適切なテーブルでは、1つの位置に2〜3個以上の要素が含まれていないため、ハッシュがうまく機能せず、ハッシュ関数を変更する必要があります。

繰り返しますが、要素数に依存しない検索です! サイズが巨大なものすべてにハッシュテーブルを使用できます。
ハッシュテーブルは、 Rabin-KarpアルゴリズムまたはKnut-Morris-Prattアルゴリズムを使用して、テキストの大きなチャンク内の文字列および部分文字列を検索するためにも使用されます。これは、たとえば科学論文の盗作の判定に役立ちます。
これで、あなたは終わることができると思います。 将来的には、 フィボナッチヒープやセグメントのツリーなど、より複雑なデータ構造を検討する予定です 。 この非公式のガイドがおもしろくて役立つことを願っています。
プログラマーが屋根裏部屋に閉じ込められたHabrに翻訳されています。