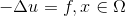
同次境界条件で
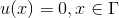
どこで
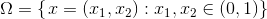
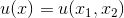
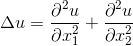
必要な検索機能
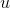与えられた方程式を解きます。
解決策
初期方程式に関数を掛ける
連続的 、 区分的に連続的に微分可能で、エッジでゼロに等しく、結果の方程式をドメイン全体にわたって積分します 
。
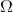部品に積分公式を適用した後、次の方程式を取得します
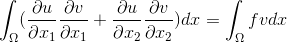
現地で紹介します
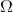ステップの正方形グリッド 
：
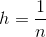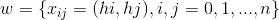
そして、各正方形を、最初の座標角の二等分線に平行な対角線で分割します。
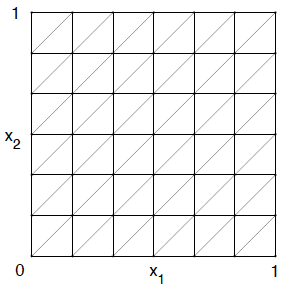
リージョンのパーティションを取得します
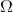三角形要素上 
-領域の三角測量 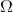。 このタイプの三角形分割は、Friedrichs-Keller三角形分割と呼ばれます。
関数としてこの方程式の近似解を求めます
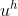境界でゼロに等しい（境界条件）、ドメインで連続 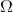そして、得られた各三角形分割要素で線形。
機能
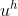次のように表すことができます。
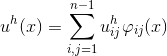
ここで、ポイントの関数の値
次のように定義されます。
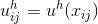
関数を置き換える
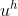変換を実行し、積分記号の下から定数を削除した最初の方程式に、各基底関数の問題を次の形式の積分の計算に還元します。
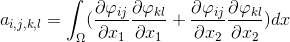
積分の符号の下の基底関数が定義の空でない共通領域を持っている場合にのみ、積分の値がゼロにならない場合があります。 構成上、各要素には3つの頂点があります。 頂点は最大6つの三角形で共有できます。
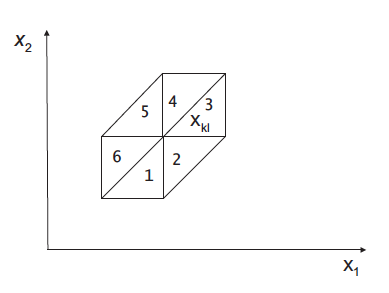
6つのケースのそれぞれに対応する導関数の値を使用します。
積分を計算した後、数値の方程式
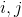次のようになります。
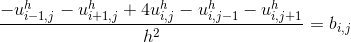
どこで
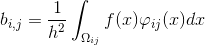
そして十分に小さい
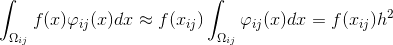
したがって、方程式は次のように書き換えることができます。
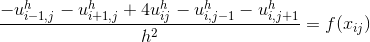
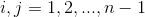
境界条件を追加することにより、すなわち：
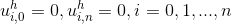
完全なSLARを取得し、それを解いて、グリッドポイントで関数の値を見つけます。
どうもありがとう。 ダウトフとM.M. 優れた文学のためのカルチェフスキー！