内容

1. テンソルとは何ですか、なぜ必要ですか？
2. ベクトル演算とテンソル演算。 テンソルランク
3. 曲線座標
4. テンソル博覧会のポイントのダイナミクス
5. テンソルのアクションとその他の理論的な質問
6. 自由固体の運動学。 角速度の性質
7. ソリッドの最終回転。 回転テンソルのプロパティとその計算方法
8. Levi-Civitaテンソルの畳み込みについて
9. 最終回転のパラメーターによる角速度テンソルの導出。 頭とマキシマを適用
10. 角速度ベクトルを取得します。 欠点に取り組む
11. 自由な動きでの体のポイントの加速。 ソリッドの角加速度
12. 固体運動学におけるロドリゲハミルトンパラメーター
13. テンソル式の変換の問題におけるSKA Maxima。 ロドリゲ・ハミルトンのパラメーターにおける角速度と加速度
14. 剛体のダイナミクスの非標準的な紹介
15. 非自由な固体運動
16. 固体の慣性テンソルの特性
17. ナットジャニベコバのスケッチ
18. ヤニベコフ効果の数学的モデリング

はじめに

最後に、かなり興味深いトピック-空間内の剛体の方向を一意に決定するパラメーターの選択-に到達しました。 歴史的に、回転角は最も人気があります-それらは主に理論力学の古典的な教科書で言及されています。









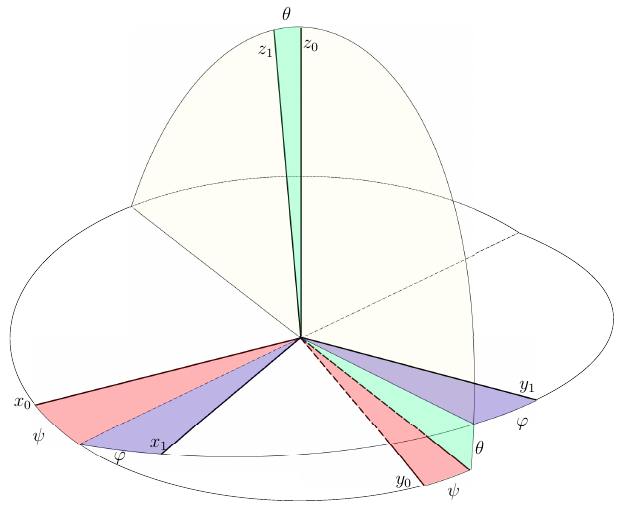
図1 オイラー角は、コンピューターグラフィックスや身体の空間運動のモデリングに携わる人なら誰でも知っているパラメーターです。 そして、彼らが知っている誰もが彼らの使用がいかに問題があるか知っています。





通常、回転角度はデカルト座標系と組み合わせて使用​​され、関連付けられた座標系は、軸を中心に3回連続して回転することでベースと組み合わせることができると言われています。 この場合、後続の各回転は、前の回転後に取得した軸を中心に実行されます。 また、次のターンは、前のターンが行われた軸に対して相対的に行われるべきではありません。 この点に関して、回転角には12の異なる組み合わせがあり、その中で最も有名なものはオイラー角です（図1）。 ベース座標系は角度だけ回転します Z軸の周り（歳差角）、次に角度 X軸の周り（章動の角度）、そして再びZ軸の周りに斜めに （適切な回転角度）を関連付けられた座標系と組み合わせる前に。



オイラー角の使用はすべての人に適しています-その数は、剛体の回転自由度の数と一致します。つまり、冗長な拘束方程式を生成しません。 しかし、図1によると、面倒な式に頼らなくても、問題の所在を推測できます。













図 2.オイラーの有名な運動方程式。 私は、やがて、彼らと一緒に長時間の骨の折れるデバッグを飲みました



オイラー運動方程式が縮退する章動角には2つの値があります（図2）- そして 。 章動角がこれらの値のいずれかをとると仮定します。歳差角と回転角は同じZ軸の周りの回転を表し、本質的に互いに区別できません。 オイラーの運動方程式を使用すると、分母がゼロになり、位相座標がNaN



になります。 彼らは到着し、統合手順は崩壊しました。



回転角度の別のオプションは飛行機の角度です： -ヨー -ピッチと -ロール（図3）。









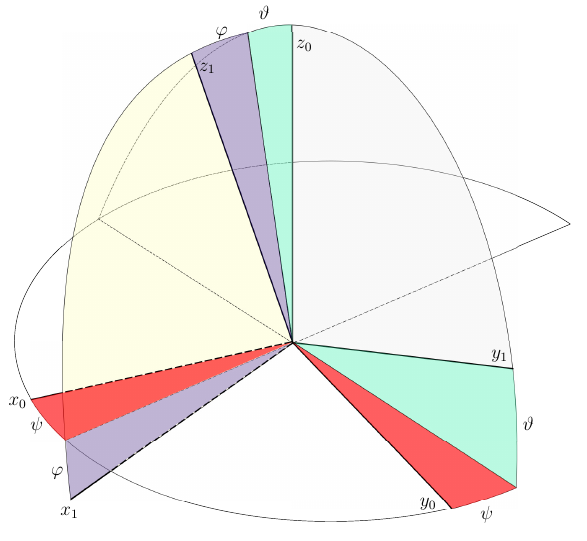
図 3.航空機の角度-宇宙での航空機の方向を決定する実用的な方法の1つ





これらの回転パラメーターはピッチで縮退します 一方、ロールとヨーは区別できなくなります。 経験の浅いシミュレーターは、急なピッチに関してギアボックスがどのようにクレイジーになるかを知っています。



回転角度のすべての可能な組み合わせは縮退しています。 方向制御システムアルゴリズムのモデリングとブックマークの範囲は、重要なパラメーター値に限定されます。 最後の記事では、最終回転のパラメーターも適切ではなく、回転テンソルのコンポーネントを直接使用することは、それらの間の過度に深い依存関係によって複雑になり、運動方程式系の高次が生じることを示しました。



しかし、偉大なレナードオイラーは、縮退性のない4つのパラメーターを導入しました。 当時の科学界は、この主題に関する彼の出版物にあまり注意を払っていませんでした。 このアイデアは、オイラーとは独立して、オリド・ロドリゲによって開発され、ウィリアム・ハミルトンの作品の中で最終的な理論的正当化を受けました。 会う-

1.四元数とそれらに対するアクション

四元数は、フォームの数です











どこで 四元数成分と呼ばれます。 数字（1）自体がハイパーコンプレックス数のセットを形成します 有効なすべてを含む 数と多くの複素数 。 ハミルトンが働いた時代の数学者は、すでに複素数について知っていて、それらに基づいて構築された方法が平面計測の問題を解決する方法を知っていました。そのような方法を空間問題に適用するために複素数の概念を拡張したいのは自然でした。 問題は、2番目の仮想ユニットを追加しても問題が解決しないことでした。 ハミルトンは、そのような拡張複素数は3成分ではなく4成分であると考えていました。 この方向で作業し、ウォークの1つにインスピレーションを与えて、彼はそのような数を掛ける規則を推測し、最終的に新生児の理論のモザイクを折りました。



したがって、四元数の乗算は、和を乗算する代数演算に縮小されますが、唯一の違いは、虚数単位の乗算の規則を決定する必要があることです。 伝統的に、二乗された虚数単位のそれぞれは-1を与えます











そして、それらのペアワイズ製品は、図で詳しく説明されています









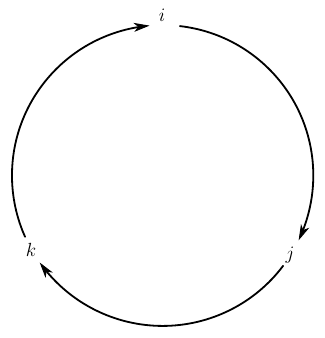
図 4.四元数の虚数単位の乗算の図





その意味は単純です-矢印で示された順序で虚数単位のペアを乗算すると、「+」記号が付いた3番目の虚数単位が得られます。 乗算の順序を逆に変更すると、符号「-」の付いた3番目の虚数単位が得られます。 デカルト座標の単位ベクトルのベクトル乗算の規則に似ていませんか？ これです、つまり、











これらのルールを使用して、2つのクォータニオンを乗算します











わあ！ 弱くないが、同様の用語を大胆に引用する











そして、確かに、ここでベクター上で痛々しいほど馴染みのあるアクションを確認できます。 ベクトルを持ってみましょう











各四元数は、スカラーとベクトルのペアとして表すことができます











とその乗算の結果











この式を、実行した乗算の結果と単純に比較し、虚数単位をデカルト基底のortと見なすことは難しくありません。 したがって、クォータニオンには3次元空間のベクトルが含まれ、たとえば次の形式のクォータニオン そして 、スカラーであり、その積はスカラー量の積と同等です











四元数種 そして ベクトル四元数と呼ばれる、およびその製品











マイナス記号付きのスカラーと、それらのベクトルのベクトル積を返します。



積の結果としてベクトル乗算が存在するため、四元数乗算の演算は可換ではありません











さて、各四元数の最後の2つの係数をゼロにすることは、複素数の積を得ると言う必要がありますか？ 私たちは複雑な分野に突入しないので、それは価値がないと思います。複素数について話しているなら、それが必要な場所です。



また、四元数の追加とそれらの数の乗算は、複雑な領域での対応する操作に似ているとは言いません。 しかし、あなたが話す必要があるのは、四元数のペアリングについてです











関連するノルム計算操作について











および逆四元数計算操作











四元数積の共役に関する別の有用な特性











さらに、逆四元数のノルムは、元のノルマの逆数です。











これらの操作は、今日ハイパーコンプレックス数を使用する理由に直接関連しています

2.線形回転演算子としてのクォータニオン

次に、このようなトリックを見てみましょう。 させる -四元数、および -別のクォータニオン。 小さな定理を証明します

ビュー変換 四元数の基準を変更しません 。

このステートメントは、直接計算によって検証されます。











実際、四元数のノルムはそのような変換によって変化しません。 四元数の場合 それがベクトル四元数である場合、それが決定されるベクトルのノルムは変更されません。 つまり、記述されたベクトル上の変換はその長さを変更せず、直交、または回転変換になります！ 小さなことは、特定のクォータニオンによって決定される、回転が発生する軸と角度を調べることです。 これを行うには、（結局、誰もこれを行う気にしない）四元数を想像してください 形で











カッコ内の値は、 量子テンソルと呼ばれます（ テンソルと混同しないでください！）。 そのベクトル部分の練習











同等の変換を行うことを誰も気にしないので、それらを行います。 代替品を紹介します











何に基づいて？ はい、これらの量の二乗の合計が常に一致するという事実については、そうであれば、誰もこれらの量を特定の角度のサインとコサインとして表すことを気にしません。 角度が2で割られるのはなぜですか？ あなたは任意の角度を取ることができるので、私たちはそれがとても欲しいので、それは私たちにとって便利になります。 導入された置換に基づいて、次の形式で四元数を書き換えることができます。











ベクトル 私たちが導入したのは独身です











それを締めくくるために、もう1つの仮定を許可しましょう-クォータニオンを単一、つまり











ここで、ベクトルクォータニオンに対して直交変換を慎重に実行します











次に、結果（2）に逆クォータニオンを掛けます











「ワニ」でテキストが乱雑にならないように、スカラーを個別に計算します











およびベクトル部分











変換結果。 最終的に、式（3）および（4）に基づいて、複雑な三角法の単純化を実行していないため、出力はベクトルであると結論付けます。











これは...ロドリゲの最終回転式です！ 変換が判明した











これは、単一の四元数に対して、逆四元数を計算する操作が共役と等価であるという事実を考慮して、次の形式で書き直すことができます。











単位ベクトルで定義された軸を中心にベクトルを回転させるのと同じ 角に 。 回転角度と回転が発生するベクトルは、上記で紹介した置換に基づいて、クォータニオンのコンポーネントから計算できます。

結論

式に従って構成された単一の四元数を確認しました











最終ターンを決定します。 与えた4つのパラメーターは、空間内の剛体の方向を一意に決定し、回転パラメーターに対して縮退しないRodrig-Hamiltonパラメーターです。 たとえば、回転角度をゼロにすると、回転軸の単位ベクトルもゼロになります。 最終角度で回転する場合、常に回転軸の位置を計算できます。



さて、しかし、窓の外で、それは夜明けしました...この記事のアウトラインはいくらか異なっていました、そして、我々はテンソルについて一言も言いませんでした。 はい、それは良いことですが、今、私たちは将来どのようなトリッキーな方向パラメーターを使用するかについて明確なアイデアを持っています。



ご清聴ありがとうございました！



継続するには...