内容

はじめに

この記事では、以前の出版物から始まったトピックを継続します。前回、テンソルの助けを借りて、角速度の性質を明らかにし、それを計算できる一般方程式を取得しました。身体に関連付けられた座標系の回転演算子から自然に派生しているという結論に達しました。

そして、この演算子の中には何がありますか？デカルト座標の場合、回転行列を取得するのは簡単であり、身体の向きを記述する何らかの方法、たとえばオイラー角またはクリロフ角を関連付けることにより、それらのプロパティを検出するのは簡単です。または、ベクトルと最終回転の角度。または四元数。ただし、これはデカルト座標用です。

テンソルについて話し始めたので、デカルト座標を放棄しました。テンソル表記法は非常に優れているため、プロパティに注目せずに便利な座標系の方程式を作成できます。そして問題は、例えば、斜めの座標の場合、回転行列は、平面の場合でも非常に複雑であることです。平面内での単純な回転のために、外観を確認する必要がありました。

したがって、この記事のタスクは、回転テンソルの内部を調べてその特性を調査し、計算のためのテンソル関係を取得することではありません。そして、タスクが設定されたら、それを解決し始めます。

1.座標系の回転テンソルのプロパティ

自由剛体の力学の問題に戻るためには、回転テンソルとは何かを理解する必要があります。テンソルのプロパティは、そのコンポーネントのセットとそれらの間の関係によって決定されます。回転テンソルは第2ランクのテンソルであり、そのコンポーネントはマトリックスで表されるため、サイクルの一般的なテーマを損なうことなく、このセクションでは「マトリックス」という用語を使用します。テンソル代数のフレームワークでは、テンソル積と畳み込みの組み合わせを扱っているため、マトリックス積の通常の「無意味な」レコードをドットで記述します。ただし、ここでも予約が必要です。「畳み込み」という用語の誤った使用を批判したため、畳み込みはテンソル乗算との組み合わせとしてよく理解されるという点を見落としました。同時に、彼らは、例えば、「Levi-Civitaテンソルでベクトルを崩壊させて...」と言い、内積の動作を参照します。

そのため、回転行列の基本的な特性を考慮します $\ mathbf {B}$

計量テンソルの回転変換は恒等変換です

$\ mathbf {B} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {B} = \ mathbf {g}$
モジュロを法とする回転行列の行列式は1に等しい

$\ det \ mathbf {B} = \ pm 1$
逆変換行列は、転置直接変換行列に似ています

$\ mathbf {B} ^ {-1} = \ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \ cdot \ mathbf {g}$
もし $\ det \ mathbf {B} = 1$ 、その後、代数補数の行列とから構築されたユニオン行列 $\ mathbf {B}$ これとその転置行列に類似しており、類似度変換は計量テンソルです

$\ mathbf {\ hat {B}} = \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {g} ^ {-1}$

$\ mathop {\ rm adj} \ mathbf {B} = \ mathbf {g} ^ {-1} \ cdot \ mathbf {B} \ cdot \ mathbf {g}$

このプロパティの結果は、上記の行列のトレースが等しいことです。

$\ mathop {\ rm tr} \ mathbf {B} = \ mathop {\ rm tr} \ mathbf {\ hat B} = \ mathop {\ rm tr} \ left（\ mathop {\ rm adj} \ mathbf {B} \右）$
もし $\ det \ mathbf {B}＆gt; 0$ 、次に、1を法とする回転行列の固有値は、形式

$\ lambda_1 = 1、\ quad \ lambda_ {2,3} = e ^ {\ pm \、i \、\ varphi}$

どこで $\ cos \ varphi = \ cfrac {s-1} {2}、\ quad s = \ mathop {\ rm tr} \ mathbf {B}$
もし $\ mathbf {u}$ 複素固有値に対応する回転行列の固有ベクトルであり、次に関係

$\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = 0$

結果：固有ベクトルの実部と虚部 $\ mathbf {u}$ 複素固有値に対応するのは直交ベクトルです

$\ mathbf {u} _ {\、r} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、i} = 0$

どこで $\ mathbf {u} = \ mathbf {u} _ {\、r} + i \、\ mathbf {u} _ {\、i}$ 。

本文ではプロパティの証明をしません-とにかくボリュームが多いと約束します。これらの証明はそれほど複雑ではありませんが、それらに興味がある人のために次のネタバレが行われました。

好奇心and盛で細心の読者向けのプロパティ1〜6の証明

プロパティ1と3は、前の記事で証明されました。特性2は、行列積の行列式の特性に依存して、特性1から簡単に証明されます。

$\ det \ mathbf {B} ^ T \、g \ det \ mathbf {B} = g$

$\左（\ det \ mathbf {B} \右）^ 2 = 1$

$\ det \ mathbf {B} = \ pm \、1$

プロパティ4は、逆行列を計算するための分析的方法に基づいています。 $\ det \ mathbf {B} = 1$ それから

$\ mathbf {B} ^ {-1} = \ frac {1} {\ det \ mathbf {B}} \、\ mathop {\ rm adj} \ mathbf {B} = \ mathop {\ rm adj} \ mathbf { B}$

$\ mathop {\ rm adj} \ mathbf {B} = \ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \ cdot \ mathbf {g}$

どこで $\ mathop {\ rm adj} \ mathbf {B}$ -ユニオン行列（代数補数の転置行列）。転置（1）、計量テンソルの対称性を使用して、

$\ mathbf {\ hat B} = \左（\ mathbf {g} ^ {-1} \ cdot \ mathbf {B} \ cdot \ mathbf {g} \右）^ T$

$\ mathbf {\ hat B} = \ mathbf {g} \ cdot \ left（\ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \右）^ T$

$\ mathbf {\ hat B} = \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {g} ^ {-1}$

どこで $\ mathbf {\ hat B}$ -回転行列の代数補数で構成される行列。関係（1）と（2）は類似関係です。同様の行列のトレースは同一です。

$\ mathop {\ rm tr} \ mathbf {\ hat B} = \ mathop {\ rm tr} \ left（\ mathop {\ rm adj} \ mathbf {B} \ right）= \ mathop {\ rm tr} \ mathbf {B}$

プロパティ5を証明しましょう。 $\ラムダ$ 固有ベクトルに対応する回転行列の固有値です $\ mathbf {u}$ 。それから

$\ mathbf {B} \ cdot \ mathbf {u} = \ lambda \、\ mathbf {u}$

この式に左側の逆変換行列を乗算します

$\ mathbf {u} = \ lambda \、\ mathbf {B} ^ {-1} \ cdot \ mathbf {u}$

プロパティ3を考慮

$\ mathbf {u} = \ lambda \、\ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u}$

回転行列と計量テンソルに実数成分があり、それらの共役が転置に減少すると仮定して、複雑な共役を実行します

$\ mathbf {u} ^ {*} = \ overline \ lambda \ left（\ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} \右）^ {*}$

$\ mathbf {u} ^ {*} = \ overline \ lambda \、\ mathbf {u} ^ {*} \ cdot \ left（\ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \ cdot \ mathbf {g} \右）^ {T}$

$\ mathbf {u} ^ {*} = \ overline \ lambda \、\ mathbf {u} ^ {*} \ cdot \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {g} ^ {-1 }$

最後の式は右側で乗算されます $\ mathbf {g} \ cdot \ mathbf {u}$

$\ mathbf {u} ^ {*} \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ overline \ lambda \、\ mathbf {u} ^ {*} \ cdot \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {u}$

$\ mathbf {u} ^ {*} \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ overline \ lambda \、\ lambda \、\ mathbf {u} ^ {*} \ cdot \ mathbf {g} \ cdot \ mathbf {u}$

最後に、方程式があります

$\左（1-\上線\ラムダ\、\ラムダ\右）\ mathbf {u} ^ {*} \ cdot \ mathbf {g} \ cdot \ mathbf {u} = 0$

次の場合にのみ当てはまります

$\上線\ラムダ\、\ラムダ= \左| \ラムダ\右| ^ 2 = 1$

それは

$\左| \ラムダ\右| = 1$

固有値を計算するには、特性方程式を作成します

$\ det \ left（\ mathbf {B}-\ lambda \、\ mathbf {E} \ right）= 0$

行列式を計算すると、この方程式の一般的な形式になります（次元（3 x 3）の行列の場合）

$\ lambda ^ 3-\ mathop {\ rm tr} \ mathbf {B} \、\ lambda ^ 2 + \ mathop {\ rm tr} \ mathbf {\ hat B} \、\ lambda-\ det \ mathbf {B} = 0 \クワッド（3）$

表記を紹介します $s = \ mathop {\ rm tr} \ mathbf {B} = \ mathop {\ rm tr} \ mathbf {\ hat B}$

$\ lambda ^ 3-s \、\ lambda ^ 2 + s \、\ lambda-1 = 0 \ quad（4）$

ファクター（4）

$\左（\ラムダ-1 \右）\左（\ラムダ^ 2 + \ラムダ+ 1 \右）-s \、\ラムダ\左（\ラムダ-1 \右）= 0$

$\左（\ラムダ-1 \右）\左（\ラムダ^ 2-\ラムダ\左（s-1 \右）+ 1 \右）= 0$

どこから

$\ラムダ_ {\、1} = 1$

二次方程式を解くことで残りの根のペアを見つけます

$\ lambda_ {2,3} = \ frac {s-1} {2} \ pm \ sqrt {\ left（\ frac {s-1} {2} \ right）^ 2-1}$

代替品を紹介します

$\ cos \ varphi = \ frac {s-1} {2}$

これは正当なものです。なぜなら、一般的な場合、根が複素共役であると仮定すると、Vieta定理により、

$\ lambda_2 + \ lambda_3 = s-1$

$2 \、\ mathop {\ rm Re}（\ lambda_2）= s-1$

または、絶対値で

$2 \、\左| \ mathop {\ rm Re}（\ lambda_2）\右| = \左| s-1 \右|$

以来 $\左| \ mathop {\ rm Re}（\ lambda_2）\右| \ le \左| \ lambda_2 \右| = 1$

それから明らかに

$\左| s-1 \右| \ le 2$

交換するとき、最終的に計算します

$\ lambda_ {2,3} = \ cos \ varphi \ pm i \、\ sin \ varphi = e ^ {\ pm \、i \、\ varphi}$

特性6の証明は、式に基づいて実行されます

$\ mathbf {u} = \ lambda \、\ mathbf {g} ^ {-1} \ cdot \ mathbf {B} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u}$

固有値モジュールの単一性と等しいことの証明で得られます。今、複雑な共役の代わりに、行列乗算の転置の特性を考慮して転置します

$\ mathbf {u} ^ T = \ lambda \、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {g} ^ {-1}$

結果の式に乗算します $\ mathbf {g} \ cdot \ mathbf {u}$ 右側に

$\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ lambda \、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {u}$

$\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ lambda \、\ lambda \、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u }$

モジュラスが1であるとすると、結果の方程式に複素共役固有値の数値を乗算します

$\ overline \ lambda \、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ overline \ lambda \、\ lambda \、\ lambda \、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u}$

$\上線\ラムダ\、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ lambda \、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u}$

私たちはついに方程式に到達します

$\左（\ラムダ-\オーバーライン\ラムダ\右）\、\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = 0$

固有値の複雑さのために、ブラケットはゼロではありません。

$\ラムダ-\オーバーライン\ラムダ= 2 \、i \、\ mathop {\ rm Im}（\ラムダ）$

それからフェア

$\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = 0$

この特性の帰結は、単純な乗算によって証明されます

$\ mathbf {u} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} = \ left（\ mathbf {u} _ {\、r} + i \、\ mathbf {u} _ {\、i } \右）^ T \ cdot \ mathbf {g} \ cdot \ left（\ mathbf {u} _ {\、r} + i \、\ mathbf {u} _ {\、i} \ right）= \ left （\ mathbf {u} _ {\、r} ^ T + i \、\ mathbf {u} _ {\、i} ^ T \ right）\ cdot \ mathbf {g} \ cdot \ left（\ mathbf {u } _ {\、r} + i \、\ mathbf {u} _ {\、i} \右）=$

$= \ mathbf {u} _ {\、r} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、r}-\ mathbf {u} _ {\、i} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、i} + 2 \、i \、\ mathbf {u} _ {\、r} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf { u} _ {\、i} = 0$

実数部と虚数部をゼロにする

$\ mathbf {u} _ {\、r} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、r}-\ mathbf {u} _ {\、i} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、i} = 0$

$\ mathbf {u} _ {\、r} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、i} = 0$

最後の方程式から、モジュールの望ましい直交性と等式が続きます $\ mathbf {u} _ {\、r}$ そして $\ mathbf {u} _ {\、i}$

なぜ回転テンソルの特性について知る必要があるのですか？

最初に、曲線座標系の回転行列がデカルト系の回転行列とどのように異なるかを読者が理解できるように、それらを完全に定式化しました。事実上、これらのマトリックスのプロパティは似ています。上記の式に計量テンソル単位の行列を置くと、直交回転行列の特性が得られます。これは、たとえばD. Yu。Pogorelovによって読み取ることができます。実際、この本は、一般的な方法で問題を検討するためにどこを掘るかを教えてくれました。

第二に、これが主なことであり、これらの行列の固有ベクトルと固有値が機械的な意味を持つことを証明します。まず、補題を証明します

させる $\ mathbf {u} _ {\、1}$ 回転テンソルの実固有値に対応する固有ベクトルであり、 $\ mathbf {u} _ {\、1}$ -対応する $\ lambda_2 = e ^ {\、i \、\ varphi}$ 、そして $\ varphi \ ne 0、\、\ pi$ 。ベクトルもしましょう $\ mathbf {u} _ {\、2 \、r}$ そして $\ mathbf {u} _ {\、2 \、i}$ 実数部と虚数部 $\ mathbf {u} _ {\、2}$ 。次に、ベクトル $\ mathbf {u} _ {\、1}$ 、 $\ mathbf {u} _ {\、2 \、r}$ そして $\ mathbf {u} _ {\、2 \、i}$ 直交ベクトルのトリプルを形成します

プロパティ6はすでに直交性について教えてくれます $\ mathbf {u} _ {\、2 \、r}$ そして $\ mathbf {u} _ {\、2 \、i}$ 。今それを証明しましょう

$\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2} = 0 \ quad（1）$

固有ベクトルの定義により

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、1} = \ mathbf {u} _ {\、1} \ quad（2）$

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、2} = \ lambda_2 \、\ mathbf {u} _ {\、2} \ quad（3）$

乗算（3）左 $\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g}$ そして変換

$\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {B} \ cdot \ mathbf {u} _ {\、2} = \ lambda_2 \、\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2}$

$\左（\左（\ mathbf {g} \ cdot \ mathbf {B} \右）^ T \ cdot \ mathbf {u} _ {\、1} \右）^ T \ cdot \ mathbf {u} _ { \、2} = \ lambda_2 \、\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2}$

$\左（\ mathbf {B} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、1} \右）^ T \ cdot \ mathbf {u} _ {\、2} = \ lambda_2 \、\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2}$

プロパティ3を考えると、

$\ mathbf {g} \ cdot \ mathbf {B} ^ {-1} = \ mathbf {B} ^ T \ cdot \ mathbf {g} \ quad（5）$

また、（2）から直接続きます

$\ mathbf {u} _ {\、1} = \ mathbf {B} ^ {-1} \ cdot \ mathbf {u} _ {\、1} \ quad（6）$

（6）と（5）が与えられると、変換（4）

$\左（\ mathbf {g} \ cdot \ mathbf {u} _ {\、1} \右）^ T \ cdot \ mathbf {u} _ {\、2} = \ lambda_2 \、\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2}$

$\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2} = \ lambda_2 \、\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2}$

$\左（1-\ lambda_2 \右）\ mathbf {u} _ {\、1} ^ T \ cdot \ mathbf {g} \ cdot \ mathbf {u} _ {\、2} = 0$

括弧内の式はゼロ以外の複素数です。これは、ステートメント（1）が真であり、検討中のベクトルが直交トリプルを形成することを意味します。

私たちが証明した補題は、任意の座標で考える回転テンソルが有限回転に関する有名なオイラー定理を満たすことを示すために必要です。

2.オイラーの有限回転定理

回転テンソルを調べたところ、ベクトルの直交トリプルがこのテンソルに直接関係していることがわかりました $\左（\ vec {u} _ {\、1}、\ vec {u} _ {\、2 \、r}、\ vec {u} _ {\、2 \、i} \右）$ 。このトリプルの最初のベクトルには興味深い特性があります-回転演算子が適用されても変化しません。確かに、結局のところ

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、1} = \ mathbf {u} _ {\、1}。 \クワッド（7）$

このベクトルは、回転しても静止したままです！そして、体が回転すると、回転軸は静止したままです。平均ベクトル $\ vec {u} _ {\、1}$ ボディに関連付けられた座標系の回転軸の空間方向を設定します。力学の過程で知られているオイラーの定理

1つの固定電流を持ち、空間内の任意の位置を占める物体の場合、固定点を通過する軸があります。この軸の周りを回転することにより、有限角度で他の任意の位置に物体を移動できます。

恒等式（7）は、この回転軸を探す場所についてのヒントを提供します。実際の固有値に対応する回転テンソルの固有ベクトルを通過します。定理を証明することでこれを検証します

体に関連付けられた座標系は、ベクトルの周りの回転によってベース座標系と組み合わせることができます $\ vec {u} _ {\、1}$ 角に $\バルフィ$ ベクトルが反時計回りの場合 $\左（\ vec {u} _ {\、1}、\ vec {u} _ {\、2 \、r}、\ vec {u} _ {\、2 \、i} \右）$ 右の3つを形成し、斜めに $-\バルフィ$ これらのベクトルが左トリプルを形成する場合

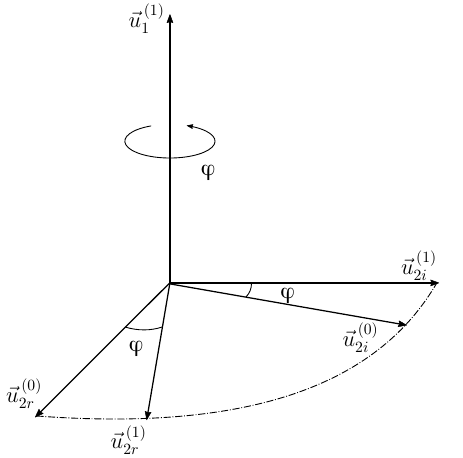
図1.有限回転の定理の証明へ

ボディに関連付けられた座標系を角度だけ回転します $\バルフィ$ ベクトルの周り $\ vec {u} _ {\、1}$ 。考慮中のベクトルは直交しているため、ベクトル $\ vec {u} _ {\、2 \、r}$ そして $\ vec {u} _ {\、2 \、r}$ 回転軸に垂直な平面で回転します。したがって、空間内のこれらのベクトルの古い位置と新しいベクトルの関係を見つけるのは非常に簡単です（図1を参照）。

$\ vec {u} _ {\、2 \、r} ^ {\、（0）} = \ cos \ varphi \、\ vec {u} _ {\、2 \、r} ^ {\、（1） }-\ sin \ varphi \、\ vec {u} _ {\、2 \、i} ^ {\、（1）} \ quad（8）$

$\ vec {u} _ {\、2 \、i} ^ {\、（0）} = \ sin \ varphi \、\ vec {u} _ {\、2 \、r} ^ {\、（1） } + \ cos \ varphi \、\ vec {u} _ {\、2 \、i} ^ {\、（1）} \ quad（9）$

式（8）および（9）は、最終回転を分析することによって取得されます。一方、変換のチェーンは、固有ベクトルの定義と回転演算子のプロパティから得られます

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、2} = \ lambda_2 \、\ mathbf {u} _ {\、2}$

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、2} = e ^ {\、i \、\ varphi} \、\ mathbf {u} _ {\、2}$

$\ mathbf {B} \ cdot \ left（\ mathbf {u} _ {\、2 \、r} + i \ mathbf {u} _ {\、2 \、i} \ right）= \ left（\ cos \ varphi + i \、\ sin \ varphi \ right）\、\ left（\ mathbf {u} _ {\、2 \、r} + i \ mathbf {u} _ {\、2 \、i} \ right）$

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、2 \、r} + i \、\ mathbf {B} \ cdot \ mathbf {u} _ {\、2 \、i} = \ cos \ varphi \、\ mathbf {u} _ {\、2 \、r}-\ sin \ varphi \、\ mathbf {u} _ {\、2 \、i} + i \左（\ sin \ varphi \、\ mathbf {u} _ {\、2 \、r} + \ cos \ varphi \、\ mathbf {u} _ {\、2 \、i} \右）\ quad（10）$

（10）の実部と虚部を等しくすると、

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、2 \、r} = \ cos \ varphi \、\ mathbf {u} _ {\、2 \、r}-\ sin \ varphi \、\ mathbf {u} _ {\、2 \、i} \ quad（11）$

$\ mathbf {B} \ cdot \ mathbf {u} _ {\、2 \、i} = \ sin \ varphi \、\ mathbf {u} _ {\、2 \、r} + \ cos \ varphi \、\ mathbf {u} _ {\、2 \、i} \ quad（12）$

（8）と（11）、（9）と（12）を比較すると、ベクトルに回転演算子を適用すると、軸の周りの回転につながると結論付けられます。 $\ vec {u} _1$ 角に $\バルフィ$

回転テンソルの内部を知ることなく、すべて（少なくとも実質的に重要な特性）を調査したため、結果は非常に印象的です。また、特定の回転テンソルの内部に特に関心はありません。主なタスクは、このテンソルを計算して、必要な角度だけ必要な軸を中心に回転させる方法を学習することです。

3.最終回転のパラメーターに関する回転テンソルの表現。フォーミュラロドリゲ

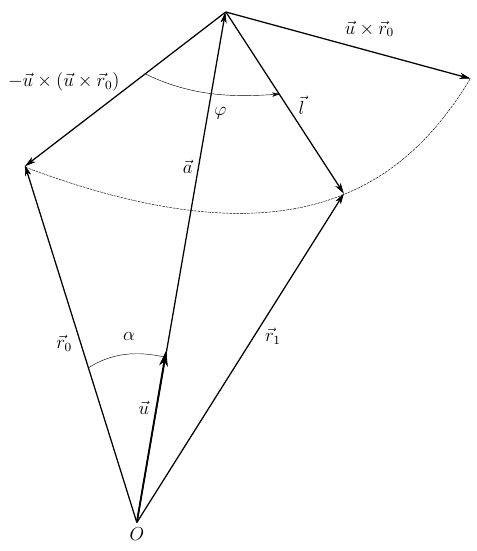
任意のベクトルの有限回転を考えてみましょう。ベース座標系では、その位置は $\ vec {r} _ {\、0}$ 体に関連する- $\ vec {r} _ {\、1}$ 。回転角 $\バルフィ$ ベクトルを通る軸の周り $\ vec {u}$ ユニットとして配置しました

$\左| \ vec {u} \右| = 1$

図 2.任意のベクトルの最終的な回転

ベクトルの関係は図2から明らかです。

$\ vec {r} _1 = \ vec {a} + \ vec {l} \ quad（13）$

どこで $\ vec {l}$ 回転軸に垂直なベクトルで、その長さは

$l = r _ {\、0} \ sin \ alpha$

ベクトル $\ vec {a}$ 回転軸に沿って方向付けられ、次のように表現できます

$\ vec {a} = a \、\ vec {u} =（\ vec {u} \ cdot \ vec {r} _0）\、\ vec {u}$

一方、以下にリストされたベクトルは同じモジュラスを持ちます

$\左| \ vec {u} \回\ vec {r} _ {\、0} \右| = r _ {\、0} \ sin \ alpha = l$

$\左| -\ vec {u} \回（\ vec {u} \回\ vec {r} _ {\、0}）\右| = l$

平均ベクトル $\ vec {l}$ それらを通して表現できる

$\ vec {l} = \ cos \ varphi \、\左（-\ vec {u} \回（\ vec {u} \回\ vec {r} _ {\、0}）\右）+ \ sin \ varphi \、（\ vec {u} \ times \ vec {r} _ {\、0}）$

ここで、書かれたベクトル関係をテンソル成分形式で書きます

$a ^ {\、m} = u ^ {\、m} \、g_ {ik} \、u ^ {\、j} \、r ^ {\、k（0）}$

$l ^ {\、m} =-\ cos \ varphi \、\ left（\ varepsilon ^ {\、mqi} \、u _ {\、q} \、\ varepsilon _ {\、ijk} \、u ^ {\、 j} \、r_0 ^ {\、k} \右）+ \ sin \ varphi \、\左（g ^ {\、mi} \、\ varepsilon {\、ijk} \、u ^ {\、j} \ 、r_0 ^ {\、k} \右）\ quad（15）$

そして2つの反対称テンソルを導入します

$U ^ {\、mi} = \ varepsilon ^ {\、mqi} \、u _ {\、q} \ quad（16）$

$U _ {\、ik} = \ varepsilon _ {\、ijk} \、u ^ {\、j} \ quad（17）$

あなたが書くことができるものを考える

$r_1 ^ {\、m} = \ left（u ^ {\、m} \、g_ {ik} \、u ^ {\、j}-\ cos \ varphi \、U ^ {mi} \、U _ {\ 、ik} + \ sin \ varphi \、g ^ {mi} \、U_ {ik} \ right）\、r_0 ^ {\、k} \ quad（18）$

テンソル（16）と（17）の畳み込みは、共通のインデックスによって、コンポーネントのマトリックスを通してペイントすることにより実行されます

$\ mathbf {\ tilde U} \ cdot \ mathbf {U} = \ frac {1} {\ sqrt g} \ begin {bmatrix} 0＆amp;＆amp; -u_3＆amp;＆amp; u_2 \\ u_3＆amp;＆amp; 0＆amp;＆amp; -u_1 \\ -u_2＆amp;＆amp; u_1＆amp;＆amp; 0 \ end {bmatrix} \ sqrt g \ begin {bmatrix} 0＆amp;＆amp; -u ^ 3＆amp;＆amp; u ^ 2 \\ u ^ 3＆amp;＆amp; 0＆amp;＆amp; -u ^ 1 \\ -u ^ 2＆amp;＆amp; u ^ 1＆amp;＆amp; 0 \ end {bmatrix} =-\ begin {bmatrix} u_3 \、u ^ 3 + u_2 \、u ^ 2＆amp;＆amp; -u_1 \、u ^ 2＆amp;＆amp; -u_1 \、u ^ 3 \\ -u_2 \、u ^ 1＆amp;＆amp; u_1 \、u ^ 1 + u_3 \、u ^ 3＆amp;＆amp; -u_2 \、u ^ 3 \\ -u_3 \、u ^ 1＆amp;＆amp; -u_3 \、u ^ 2＆amp;＆amp; u_1 \、u ^ 1 + u_2 \、u ^ 2 \ end {bmatrix} \ quad（19）$

（19）が同等であることは簡単にわかります

$U ^ {\、mi} \、U _ {\、ik} =-\左（\ delta_k ^ {\、m} \左| u \右| ^ 2-u_m \、u ^ {\、k} \右）=-\左（\ delta_k ^ {\、m}-u ^ j \、g_ {jm} \、u ^ {\、k} \右）\ quad（20）$

（20）を考慮して（18）を変換します

$r_1 ^ {\、m} = \左[u ^ {\、m} \、g_ {jk} \、u ^ {\、j}-\ cos \ varphi \、u ^ {\、j} \、g_ {jk} \、u ^ {\、m} + \ cos \ varphi \、\ delta_k ^ {\、m} + \ sin \ varphi \、g ^ {mi} \、U_ {ik} \ right] \、 r_0 ^ {\、k} \ quad（21）$

（21）から、回転演算子の式を取得します

$B_k ^ {\、m} = u ^ {\、m} \、g_ {jk} \、u ^ {\、j}-\ cos \ varphi \、u ^ {\、j} \、g_ {jk} \、u ^ {\、m} + \ cos \ varphi \、\ delta_k ^ {\、m} + \ sin \ varphi \、g ^ {mi} \、U_ {ik} \ right \ quad（22）$

どこで

$U_ {ik} = \ varepsilon_ {ijk} \、r ^ {\、j}$

-回転軸の単位ベクトルによって生成されたランク（0.2）の非対称テンソル。

または、非コンポーネント形式

$\ mathbf {B} = \ mathbf {u} \ cdot \ mathbf {u} ^ T \ cdot \ mathbf {g}-\ cos \ varphi \、\ mathbf {g} \ cdot \ mathbf {u} \ cdot \ mathbf {u} ^ T + \ cos \ varphi \、\ mathbf {E} + \ sin \ varphi \、\ mathbf {g} ^ {-1} \ cdot \ mathbf {U} \ quad（23）$

式（22）および（23）は、ロドリゲ回転式と呼ばれます。任意の非縮退メトリックを持つ座標系でそれらを取得しました。

おわりに

上記のすべては、1つの目的-任意の座標系の回転演算子の式を取得すること-のために考慮されました。これにより、角速度のテンソルと擬似ベクトル、そして角加速度を（23）で表現できます。その後、空間内の立体の向きを特徴付けるパラメーターを選択し（これらはロドリゲハミルトンパラメーターです。はい、四元数について説明します）、一般化された座標で立体の運動方程式を書き留めます。 , , , .

ご清聴ありがとうございました！

継続するには...

テンソル代数の魔法：パート7-ソリッドの最終回転。回転テンソルのプロパティとその計算方法

内容

はじめに

1.座標系の回転テンソルのプロパティ

2.オイラーの有限回転定理

3.最終回転のパラメーターに関する回転テンソルの表現。フォーミュラロドリゲ

おわりに

More articles:

テンソル代数の魔法：パート7-ソリッドの最終回転。 回転テンソルのプロパティとその計算方法

内容

はじめに

1.座標系の回転テンソルのプロパティ

2.オイラーの有限回転定理

3.最終回転のパラメーターに関する回転テンソルの表現。 フォーミュラロドリゲ

おわりに

More articles:

テンソル代数の魔法：パート7-ソリッドの最終回転。回転テンソルのプロパティとその計算方法

3.最終回転のパラメーターに関する回転テンソルの表現。フォーミュラロドリゲ