100年後：ラマヌジャンの記録のギャップを埋めた

オレグ・マリチェフとマイケル・トロットの投稿「 100年後、ラマヌジャンのギャップが埋められた」の翻訳。

記事のテキスト、インタラクティブモデル、および記事で提供されるすべてのコードを含むファイルは、こちらからダウンロードできます。

翻訳に協力してくれたキリル・グゼンコに深く感謝します。

---

100年前、 Srinivasa RamanujanとG.H. Hardyは、数学におけるこのような驚くべきことについて有名な通信を開始し、Hardyはこれを信じることがほとんど不可能であると述べました。 1913年5月1日、ラマヌジャンはケンブリッジ大学で恒久的な地位を得ました。 5年後のある日、彼は王立協会の研究者となり、彼のグループは当時世界で最も権威のある科学グループになりました。 1919年、ラマヌジャンは2月27日から3月13日にかけて行われたインドへの名古屋汽船での長い航海中に死亡しました。 彼が持っていたのはノートとペンだけで（その時点ではMathematicaはありません）、彼の死の前に方程式を紙に残したかったのです。 彼は多くの機能に対する解決策を持っていると主張したが、数学の他の分野に移る前に書き留める時間しかなかった。 彼は次の不完全な方程式と14の他の方程式（下記参照）を書き留めましたが、現在解決されているのはそのうち3つだけです。







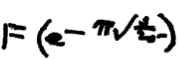
彼はおそらく肝性アメーバ症で数ヶ月間死んでいた。 彼の最後のノートはマドラス大学からG.H.ハーディに送られ、G.H。ハーディはそれを数学者G.N.ワトソンに譲渡しました。 ワトソンが亡くなった1965年に、大学長は彼のオフィスでノートを見つけ、破壊する書類を選択しました。 ジョージ・アンドリュースは1976年にこのノートブックを再発見し、1987年にようやく出版されました。 Bruce BerndtとAndrewsは、 失われたラマヌジャンノートブックについて、一連の本（ パート1 、 パート2 、およびパート3 ）で書きました。 ベルントが言ったように、「この「ノートブックの発見」はノートブックを失いました。それが数学の世界にブームを引き起こしました。それは音楽の世界でベートーベンの第10交響曲の始まりを引き起こしたでしょう。」



ラマヌジャンの結果を分析した彼の本で、ベルントは、 ただし、この決定は特にエレガントではないことに注意してください。 以下に示すように、ラマヌジャン自身が見つけた他のソリューションと同じくらいエレガントなソリューションがあります。







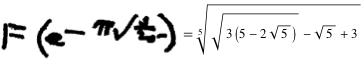
この方程式はどういう意味ですか？ 算術 的進行と幾何学的進行を比較することから始めましょう。



特定の算術級数の最初のnメンバーの合計： 1 + 2 + 3 + ... + n



特定の等比数列の最初のnメンバーの合計： a ¹ + a ² + a ³ + ... + a ⁿ



進行の各タイプについて、上記の式を閉じた形に縮小すると、部分和式を使用してその動作を予測できます。



算術級数の別の形式を次に示します。これは連続分数の形式で表されます。







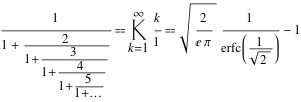
シンボルはどこですか MathematicaのContinuedFractionK関数に対応します。



同様に、連続分数の「幾何学的」バージョンは、ロジャース・ラマヌジャンR関数として知られています 。 これは、ロジャース・ラマヌジャンのS関数に関連しています（ レナード・ジェームズ・ロジャースは 1919年にラマヌジャンとともに出版されました）。 「失われたノートブック」では、 F （ q ）はS （ q ）として表されます。



R （ q ）は、次の形式の連続した部分です。







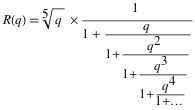
S （ q ）についても同様です。 （乗算器を使用する 数式をより「便利」にします）。 より正式な定義は次のとおりです。











これらの機能は 。 多くの公開された作品はS （ q ）=- R （ -q ）に言及していますが、これは複雑なドメインのルートのマルチリーフの性質のために真実ではありません。 Pohhammer q-charactersを介してRとSを指定して、計算を大幅に高速化することもできます。











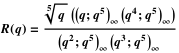
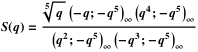
以下は、複素平面上の単位circlekにおける関数Rの振る舞いを示しています。 得られた値は複雑になる可能性があるため、関数R （ q ）の実数部、虚数部、引数、および絶対値（Im、Re、Arg、Abs）が表示されます。 単位円自体は、この関数の分析の自然な境界であり、関数R （ q ）の多くの特徴を含んでいます。 ご覧のとおり、ロジャース・ラマヌジャンの機能は、数学的な特性だけでなく、視覚的にも美しいものです。







関数RおよびSは、連続分数に関連付けられた少数の名前付き関数のうちの2つです。 最近、関数RとSの定理と公式を収集しました。これには、ラマヌジャンの「失われたノート」からの不完全なものも含まれます。 最後の行は同等です 。







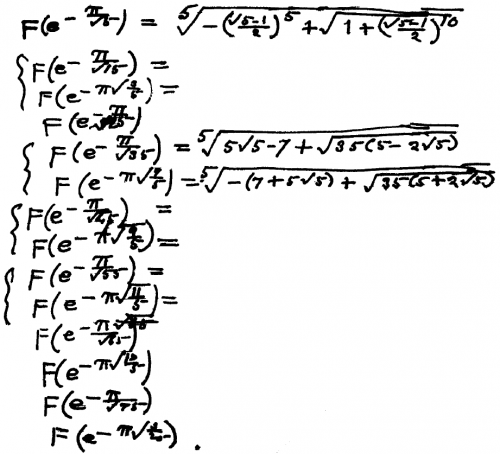
それらの多くは、ラマヌジャンの後に再発見されました。 それらはすべてMathematicaで簡単に解決できます。 以前に登場したものから始め、Oleg MarichevがMathematicaで最初に実装したものから始めて、いくつかの有名なソリューションを紹介します。







ブルース・ベルントは次のように述べています。 値によって決定できます そして、 R （ q ⁵ ）とR （ q ）をリンクする有名な方程式。 あまりエレガントではないので、ここでは得られた値を示しません。」



Simplify 、 RootReduce、およびその他の多くのMathematica関数を使用すると、大きな方程式を最もエレガントな形に縮小できます。 ラマヌジャンはチョークと知性を使って結果を単純化しました-彼はリストからかさばるものを消去し、優雅なものを残しました。 ラマヌジャンは実際にエレガントな解決策、または少なくともそれを見つける方法を知っていたようですが、それを書き留める時間はもうありませんでした。 使用した方法は次のとおりです。 まず、関心のあるポイントで数値を取得する必要があります。 次に、この数値に対して閉じた代数形式を取得する必要があります。 次に、結果の代数的数をラジカルの構築を通して表現します。 次に、結果のフォームを元の値と非常に高い精度で数値的に確認する必要があります。































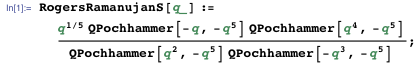
つまり、目的の形式の数値が関数の値と同じであることを確認します。 値は少なくとも最初の10,000桁と一致します。











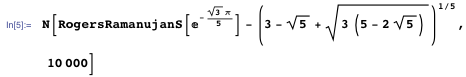
どちらも非常にエレガントな形式の代数的数であるため、これは非常に説得力のあるテストです。 また、この方法は、 S （ q ）およびR （ q ）の現在未知の多くの値を検索するために簡単に一般化できます。



実際の証明は、モジュラー方程式によって実装できます。 これは、 Sの 5次のモジュラー方程式です。











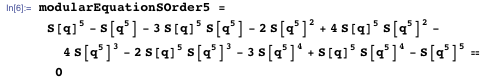
既知の値を使用します S （ q ⁵ ）の場合、 S （ q ）の方程式を解いて値を取得します 。



















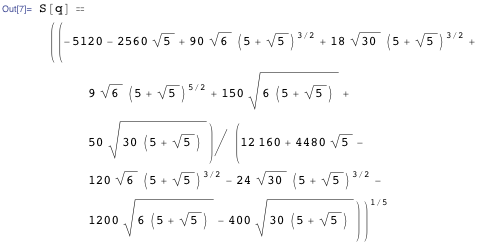
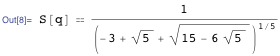
分母を取り除くと、以下の結果が得られます。











ラマヌジャンの方程式は、最近の研究とテーマが似ており、 Wolfram | Alphaの連続分数に関する多くの異なる知識を追加します。 次の投稿の1つで、 連続分数K（1、n、{n、1、inf}）のクエリの入力などの新機能について説明します。



また、インタラクティブなデモ「 Ramanujan R and S 」で数百の正確な値のリストを作成しました。







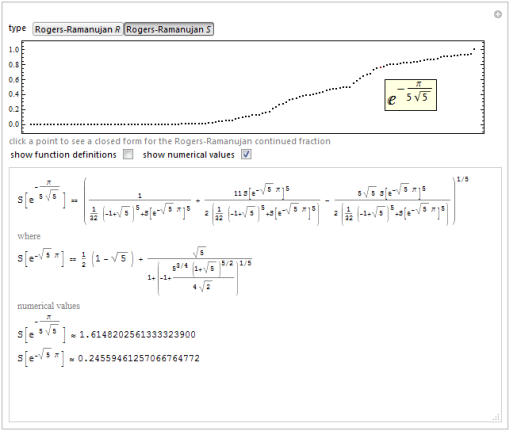
「非常にエレガントではない」とは、ラマヌジャンの作品については決して言えないことです。 そして、私たちは彼のアイデアがどれほどエレガントであったかを喜んで示しました。