ロシア連邦の市民のパスポートの例を考えてみてください。定期的なホログラフィックパターンが見やすくなっています。
そのようなパターンを見つけることを学ぶと、最大の有用な情報を保持するために、画像全体ではなく、これらの要素が存在する場所でのみセキュリティ要素を削除するアルゴリズムを使用することが可能になります。そのようなアルゴリズムは多くの場合、画像の有益なセクションの品質を低下させるためです。 さらに、認識システムは、セキュリティ要素がシンボル領域に配置されているという事実を使用して、設定を変更したり、結果の信頼度を下げたりすることができます。
この記事では、フーリエ変換を使用して周期的パターンの存在（検出）を判定する方法について説明します。これは、ロシアのパスポートでホログラフィックパターンを検出するのに良い結果を示しました。
画像モデル
まず、1次元のケースのモデルを示します。このモデルは、2次元のケースに簡単に移行できます。
I（x）を長さNの元の画像とし、他の2つの画像で構成される：背景画像h（x）と周期的パターンg（x）を含む画像：
通常、ドキュメントの背景はテキスト情報以外のすべてです。 この場合、背景は定期的なテンプレートを除くすべてです。
テンプレートを構成する単一コピー（ロシア連邦のパスポート上の1つの「イーグル」の画像）の数は事前にわかっており、Mに等しいと想定できます。均等に分布している場合、それらの期間はT = N / Mになります。その後、テンプレートの画像はg（x ）は、対応する値でシフトされた単一コピーf（x）の合計で表すことができます。
ただし、パターンg（x）はより便利な方法で表すことができます。 信号処理は、しばしばデルタ関数を使用します
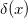x = 0で1に等しく、それ以外の場合はゼロ。 次に、その人気を決定するものを例で示します。
周期Tのデルタ関数の合計で構成される関数c（x）を考えます。そのデルタ関数は、対応するテンプレートインスタンスf（x）が配置されている場所にあり、他の場所にはゼロがあります。 このような関数は、Dirac comb（Dirac comb、コームを連想させるため）またはImpulse trainと呼ばれます。
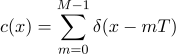
図は、N = 256およびM = 8（T = 256/8 = 32）のディラッククレストの例を示しています。
次に、パターンg（x）の周期信号は、パターンf（x）の1つのインスタンスとディラッククレストc（x）の畳み込みとして表すことができます。
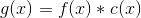
確かに、1つの文で「周期的」と「畳み込み」という言葉を使用したばかりの人は誰でも、フーリエ変換について話し始めるでしょう。
周期的パターンの離散フーリエ変換
g（x）の離散フーリエ変換（DFT）を
元の信号を構成します。
フーリエ変換の最も重要な特性の1つは畳み込み定理です。これにより、元の信号の畳み込みのフーリエスペクトルは、フーリエスペクトルの積になります。
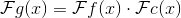
DFTはディラックの紋章とは別に考慮します
。 1つのデルタ関数のDFTは次と等しいことが知られています。
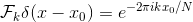
DFTは線形変換です。 デルタ関数の合計のDFTは個々のデルタ関数のDFTの合計であるため、次のように記述できます。
のような：
統合出展者
から定期的に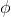 
期間あり 
、そして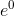 
1に等しい。 Mのk個の倍数（k = 0、M、2M、...）の場合、合計の各メンバーが1に等しくなり、Mのすべてのメンバーに等しくなるため、合計はMになります。kのその他の値（ Mの倍数） 合計のすべてのメンバーが相互に破棄されるため、ゼロに等しくなります。 この事実を証明することに興味がある場合は、間隔を空けて円上にMポイントを描画してみてください 
（m番目の点の角度 重要な事実を得ました-均一に分布したデルタ関数の合計Mのフーリエ変換は、デルタ関数の合計（Mで乗算）ですが、すでに周期Mがあります：
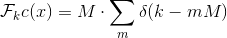
言い換えると、M = 8のデルタ関数が前の図の元の信号に適合する場合、信号長に関係なく、DFTは図に示すように8ポジションごとに「ピーク」を持ちます（虚数部は常にゼロに等しい）。
畳み込み定理から得られた式に戻ります。 周期的テンプレートの全スペクトル（位置/周波数k）<// tex.s2cms.ru/png/%5Cmathcal%7BF%7D%20g(x） "title =" \ mathcal {F} g（x） "/>均等に分布したピーク位置を除き、どこでもゼロに等しい関数を持つ製品製品全体が同様の形をしていることがわかります。
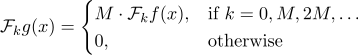
したがって、DFTだけを見ると、周期的な信号を簡単に「認識する」ことができます。
周期的パターンの画像をシフトするときのDFT
これまでのところ、テンプレートの最初のインスタンスは常にゼロ座標にあると仮定しましたが、もちろんそうであるとは限りません。 さらに、デルタ関数の合計のシフトされた信号のDFTは、以前に示したデルタ関数の別の合計ではないため（非ゼロの虚数部が現れ始めます）、シフトされた周期信号を単純に検出することはできません...または、できますか？ 幸いなことに、この状況から抜け出す簡単な方法があります。
DFTの各複素数は単一の高調波の振幅と位相シフトをエンコードし、位相シフトのみがシフト中に変化し、振幅は同じままであることを思い出してください。 さらに、信号がゼロから始まる場合、その位相シフトはゼロに等しく、実数部のみで構成されるため（虚数部はゼロに等しい）、その振幅はそれ自体に等しくなります。 最初の信号がシフトされた場合でも、そのDFTだけでなくDFTの振幅を見ることができ、シフトがない場合に表示されるものと同じものを常に見ることができます。
二次元の場合
周期的なパターンを検出する必要のある2次元画像の場合、状況は非常によく似ています。垂直周期が水平周期に追加され、DFTに「ピーク」のある画像がまだありますが、現在は2次元です。 たとえば、5x4ガウス格子の場合、DFTの振幅は次のようになります。
----> DFT ----> 
DFTのピーク間の水平距離は5で、垂直距離は4です。これは、元の画像の「適合」標本の数に等しくなります。
ロシア連邦のパスポートでは、周期的なホログラフィックパターンは少し異なり、チェス盤のように見えます。
----> DFT ----> 
DFTの振幅も、垂直と水平のピーク間の距離が4のチェス盤に似ていますが、水平と垂直自体は2ピクセルごとに通過します。 これは、チェス盤が2つのグリッドの合計として表され、その1つが斜めにシフトされるためです。 DFTは線形であるため、チェス盤のDFTは格子のDFTの合計になります。
これで、画像内の周期的なパターンの直接検出を開始するために必要なすべての知識が得られました。
定期的なパターン検出
この方法の主なアイデアは、画像のDFTの振幅をチェックし、予想されるピーク構造が含まれていることを確認することです。
最初のステップは、ホログラフィック要素から同じ「チェスボード」を含む画像の領域を切り出すことです。各水平および垂直に正確に2つの要素があります。 これらの要素がどのようにシフトされるかは気にしないので、適切なサイズの任意の領域を使用できます。 ただし、たとえば、写真付きのパスポートの領域の代わりに、少量のノイズとテンプレートがはっきりと見える画像の領域を選択すると便利です。
5％の誤差でもDFT振幅のイメージを大きく損なう可能性があるため、信号が周期的でなくなるため、領域の必要なサイズを非常に正確に決定することが重要です。
次のステップでは、テンプレートの各インスタンス間の差異を最小限に抑え、背景をできるだけ単調にし、テンプレート以外のすべて（テキスト、行など）を削除します。
最も簡単な方法は、画像のサイズを大幅に縮小することです。 私たちの場合、元のサイズが910x938であったとき、56x58に縮小しました。 画像の両側に16回。 さらに、モルフォロジカルクロージャを使用して、画像のテキストやその他の小さな詳細の残りを削除できます。
----> 
----> 
最後に、中心付近で処理された画像からDFTの振幅がどのように見えるかを確認します。
----> DFT ---->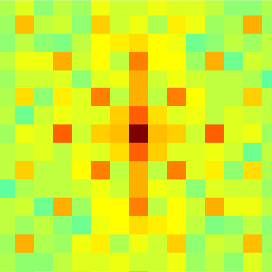 
この図は、予想されたピークの構造を明確に示しています。 明確にするために、最初にホログラフィックパターンがなかったパスポートの画像の領域からのDFTの例を示します。
----> DFT ----> 
前述のピーク構造はここにないことがわかります。
ピーク構造の存在を確認するために、非常に単純なアルゴリズムを使用しましたが、それでも優れた結果が示されました。
位置の中心に最も近いいくつかの潜在的なピーク（たとえば、3）を考慮し、各位置について、ピークの値とその8つの隣接値の間の最小差（モジュールを使用しない）を計算します。 これは、これがピークでない場合、最小差は負になるという考えです。 次に、各ピークについて得られた最小値の平均を計算し、それをしきい値（たとえばゼロ）と比較します。 平均がしきい値よりも大きい場合、画像に目的のピーク構造が存在すると考えられます。
メソッドの複雑さ
メソッドの主な手順とその複雑さをもう一度説明しましょう。
- 画像サイズをNからNに縮小する*：O（N）
- サムネイル処理：O（N *）
- 高速離散フーリエ変換：O（N * log N *）
- フーリエスペクトルの振幅でのピーク構造の存在の分析：O（1）
すべての画像処理とそれに続く離散フーリエ変換は、大幅に縮小された画像で行われ、さらに元の画像サイズに関係なく一定のサイズN *を持つことに注意することが重要です。 したがって、他のすべてが定数になるため、アルゴリズムの複雑さはO（N）です（Nは元の画像のサイズ）と数えて言うことができます。
N *は非常に小さい（約3250ピクセル）ため、最も時間のかかる操作は実際に画像サイズを縮小することであり、元の画像サイズから線形時間で動作しますが、実際には漸近的に改善することはできません（画像を何らかの方法で読み取る必要があります）。
結果
ロシアのパスポートのスキャン画像で3セットを使用しました。そのうちの1つはポジティブです。 ホログラフィックパターンを含む画像を含み、他の2つはネガティブです。 ネガティブセットの最初のセットには、ロシア連邦のパスポートと印刷されたテキストが含まれ、2番目のセットには手書きのパスポートが含まれていました（はい、まだ存在しています）。
| データセットの説明 | 画像の数 | 受け入れられた | 拒否されました |
|---|---|---|---|
| ポジティブ | 484 | 99.38％ | 0.62％ |
| 負の入力テキスト | 522 | 1.72％ | 98.28％ |
| 負の手書きテキスト。 | 204 | 0.00％ | 100.00％ |
パラメータの微妙な「適合」を行っていませんが、偽陽性と偽陰性の結果の割合は非常に低いことがわかります。
おわりに
DFT画像分析を使用して、ドキュメント画像上の周期的なパターンを検出する方法を提案し、ロシアのパスポートでの成功したアプリケーションを示しました。
私たちの方法は、検出の問題を解決します。 画像内の周期的なパターンの存在の質問に対するyes / noの答え。 しかし、陽性検出後にこのテンプレートのすべての要素が正確にどこにあるかを示すようにメソッドを拡張することは可能ですか？ はい、可能です。これを行うことができます。また、フーリエスペクトル（振幅ではなく、現在の位相）を分析することもできます。