はじめに
コンピューター数学(SKA)システムは驚異的に機能します。 数学パッケージの開発は、思考が思わず忍び寄るところに達しました。そして、表現を変換する「汚い」作業のほとんどを機械の肩に移すことができるなら、なぜ学校や大学で数学(または物理学、力学)を教える古典的な方法が必要なのでしょうか? また、問題の分析的な解決策を得ることができない、または困難な場合は、人気のあるパッケージのいずれかで数値的に「ニブル」にしないでください。 したがって、生徒の理解レベルを初期の方程式系の編集に限定しましょう。しかし、教えることは決めません。すべてのことはコンピューターによって簡単に簡単に行われます。
この記事を書くきっかけは、 V.I。アーノルドの本から引用した 、ハイキングが好きな2人の老婦人の問題に関する記事だったことを隠しません。 この点で、アイデアは単純な数学的問題を検討するために考え出されましたが、その解決策はSKAの能力がかなり規則的な上限にしばしば立ち向かうことを示しており、さらなる分析に適したコンパクトな解決策を得るには、回を少し緊張させる必要があります。
1.三角方程式のシステム
それほど遠くない2003年に論文の仕事を始めたとき、次の形式の三角方程式のシステムを解く必要に直面しました。
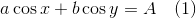

パラメーターa、b、A、Bは正です。 条件は方程式の根に課されます

そのようなシステムはどこで発生しますか? たとえば、閉じた4リンクの運動学を計算する場合。 このような閉じた4リンクは私の作品の中にありました。ほぼ1年前に私が「会議」を作ることに着手したときと同じものがありました(彼の仕事で教授を助けました)。
その後、2003年に、私はMapleシステムに精通しただけで、その機能に喜びを感じました。当然、このシステムを任せました。 そして、「残念」が私を待っていました... Maple 18とMathematica 10が今日このタスクに与えるソリューションを見てみましょう。
2. SKAの「額」の問題の解決
私のお気に入りのMapleでは、方程式系を設定します
restart; eq01 := a*cos(x) + b*cos(y) = A; eq02 := a*sin(x) - b*sin(y) = B;
そして解決しよう
solv := solve({eq01, eq02}, {x, y});
そして取得...
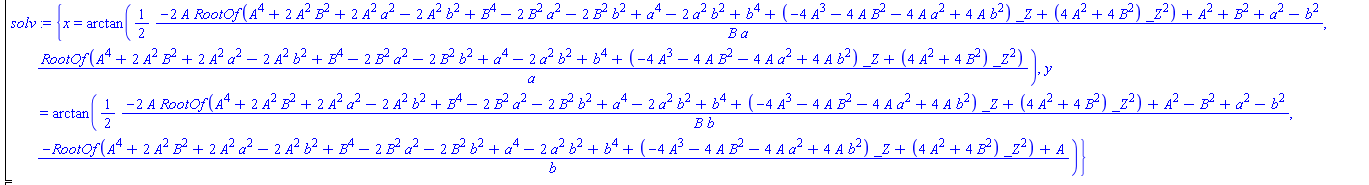
このbyakはオンラインLaTeXに適合しなかったため、スクリーンショットを提供する必要がありました。 この結果は、問題の記述が一般的すぎるという事実によるものです。 条件(3)を使用して、システムに関心のあるソリューションを示す必要があります。
solv := solve({eq1, eq2, x > 0 and x < Pi, y > 0 and y < Pi}, {x, y});
この場合、結果はより良く見えます。

もう一度、私は不器用なスクリーンショットについて読者に謝罪し、システムに2つの解決策が得られたことに注意します(1)-(3)、今は問題の機械的な意味に対応する答えを見つけ出す必要があります(それはあります) a、b、A、およびBの背後には、かなり重要な表現(もちろんxとyに依存しない)が潜んでいる可能性があります。
Mathematica 10は、画面上にあるいくつかの一般的な解の有限形式を受け取るという意味で、これらの方程式を使用する方が適切です。

システムに条件(3)が追加されている場合、Wolframは、Solve [...]にはそのような場合の解決方法がないことを伝えます(この問題に関するヒントを読者に感謝します。話を続けます)。
さらに、両方のSKAはソリューションで偽のアークタンジェントを提供しますが、これはさまざまな理由で必ずしも便利ではありませんが、これについては説明しません。それぞれの場合で異なる理由があります。
私の晩年の「シェフ」が2003年にこれらの決定を見たとき、彼は「これらのワニをとかしなければならない」と考えて言ったので、私はさらなる思考に陥った。 そして再び私は一枚の紙と鉛筆で武装しました...
3. SKA +脳
十分にコンパクトなソリューションを得るには、システム(1)-(3)を未知数に関して線形に変換する必要があります。 これを行うには、三角法の学校知識を使用します。
そこで、方程式(1)と(2)を二乗して追加し、xとyに依存しないすべてのものを方程式の右側に移動します。
left1 := lhs(eq01): left2 := lhs(eq02): right1 := rhs(eq01): right2 := rhs(eq02): eq03 := simplify(left1^2 + left2^2)= right1^2 + right2^2; eq03 := eq03 - (a^2 + b^2); left3 := combine(lhs(eq03)); eq03_1 := left3 = rhs(eq03);
式「合計の余弦」を使用して、新しい方程式を取得します
今、未知数の合計に関してそれを解決すると、線形方程式に到達します
線形方程式はアフリカでも線形です-未知のものを見つけると、別のものが得られます。 別の未知のものを扱い、それらの方程式の1つからxを削除します。 条件(3)があるので、明らかに
これにより、プラスマイナスのあいまいさなしに基本的な三角関数のアイデンティティを使用する機会が与えられます
コサインXは最初の方程式から取られます
したがって、サインx
紙をパフしないように、これをすべてMapleに任せます
eq01_1 := subs(cos(x) = u, eq01); slv := solve(eq01_1, u); eq02_1 := subs(sin(x) = sqrt(1-slv^2), eq02); eq02_1 := eq02_1 + b*sin(y);
出力方程式を持つ
方程式(7)は二乗し、いくつかの変換が必要です
left := expand(lhs(eq02_1)^2): right := expand(rhs(eq02_1)^2): eq02_2 := collect(simplify(right - left), b); eq02_3 := subs(coeff(eq02_2, b) = tmp, eq02_2); slv2 := solve(eq02_3, tmp); eq02_4 := -2*A*cos(y) + 2*B*sin(y) = slv2; eq02_5 := eq02_4/(-2);
形の方程式になる
そして今、私たちは、多くの人に知られている「フェイントイヤー」を実行します
left2 := lhs(eq02_5); left3 := subs(A = O2A*cos(xi), B = O2A*sin(xi), left2); left4 := subs(O2A = sqrt(A^2 + B^2), combine(left3));
つまり、方程式の両側を
新しい方程式が得られ、
yについて問題なく解く
eq02_6 := left4 = rhs(eq02_5); slv3 := subs(xi = arccos(A/sqrt(A^2 + B^2)), solve(eq02_6, y)):
ご覧のとおり、ゲームは非常にコンパクトになりました。 式(5)に戻り、xを見つけます。
そして今、上記の「ワニ」と比較して、
結論
コンピューター代数システムは現代の科学者の不可欠なアシスタントであり、人生を簡素化し、紙のソリューションの「シート」に身を埋める必要をなくし、迷惑なエラー/説明を排除し、生産的な活動のために脳を解放します。 しかし、それらのアプリケーションの成功は、一般的な数学的文化と基本的な事柄の知識から切り離せません。 そうでなければ、ほとんど表面にあるソリューションは、光をまったく見る機会がありません。
私の著作にご注目いただきありがとうございます!