複雑な素数

この記事の著者は、幾何学的に見れば、素数の集合を構成するものを垣間見ることができます。 これはプロの仕事ではなく、いくつかの興味深いパターンの単純で素人的な研究です。 したがって、この記事には複雑な数学は含まれず、そのジャングルに深く入り込むことはありません。 一般に、素数、その構造、および数論の分野における数世紀にわたる研究にあまり精通していない場合は、この記事が役立ちます。







私は特に、資格のある数学者とそれらを特定する読者のために強調します：この記事は専門的な仕事ではありません。 これは、明確にするためだけでなく、分析的にさらに表現できる構造のパターンの強調を強調するために、複合数のいくつかのプロパティとパターンの図解です



読者はおそらく素数に関連する多くの問題を知っているでしょう。 自然数の集合におけるそれらの位置は明らかではありません。 大きな素数を見つけるのは難しく、簡単にするために大きな数をテストするには多大な労力が必要です。 多くの最新の暗号化方法は、この困難に基づいています。 はい、多値素数を簡単に掛けることができますが、結果を知って、元の因子を見つけることは非常に難しい作業です。



単純な反復よりもはるかに高速な最適化方法が数多くありますが、最適化によって検索が10倍高速化された場合でも、数値を小数点以下2桁（つまり100倍）増やして検索を100倍遅くすれば十分です。



これは、アルゴリズムの複雑さが指数関数的であることを意味します。したがって、スーパーコンピューターがどれほど高速であっても、数の長さをさらに選択できるため、10億台のスーパーコンピューターが必要になります。 確かに、もう一度明確にする価値があります。乗算のための素数を見つけるために、それはますます難しくなります。



ところで、数学者は、複雑さが指数関数的に数の長さに依存しない分解アルゴリズムを見つけることが不可能であるという事実の証拠も反論も見つけませんでした。 そして、これを証明または反論したことで、一部の数学者は信じているように、同時にリーマン仮説として知られている数学的問題を解決することができます。 クレイの数学研究所は、それを証明するために100万ドルを約束しています。 因数分解問題は多項式であることが判明するかもしれませんが、リーマン仮説を証明したり反証したりすることはありません。

数字は影を落としますか？

素数を簡単に見つけることができる規則性はわからないので、複合数の規則性を詳しく見ていきますか？ 数学的に言えば、素数のセットに追加される自然数のセットを考慮します。



化合物番号の考え方は非常に簡単です。 いくつかの正の整数を取り、それらを乗算します。 したがって、複合数を取得します。



nに2を掛けるだけで、複合数の無限大を簡単に見つけることができます。







3を掛ける場合も同様です。







それは4に続きますが、ここでは新しい数字は見つかりません。それらはすべて2nに既に等しくなっています。 次に、5n、6nの順に進みます。2nと3nが同時に2回見つかっています。 これは複合数の数を増やすことはありませんが、複合数の法則は素数の積にあるという考えにつながります。



しかし、もう少し進んでみると、興味深いパターンが見つかります。数字6は2と3の積です。これは、テーブルに便利な多数の合成数があることを意味します。







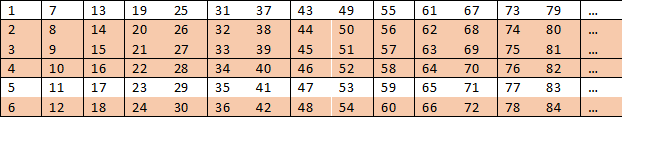
表を見ると、2、3、4、および6行目には素数があり得ないことがわかります。 つまり、素数を見つける確率は2/6を超えることはできません。 数字はさらに低い可能性があることを理解していますが、どれくらいですか？



複合数の便利な構造をさらに検索してみましょう。これについて、2x3 = 6の意味を考えますか？ 2x3x3の作品をベースにするとどうなりますか？ 次の興味深いテーブルを取得します（スペースをあまり使用しないように、フォントを減らします）。







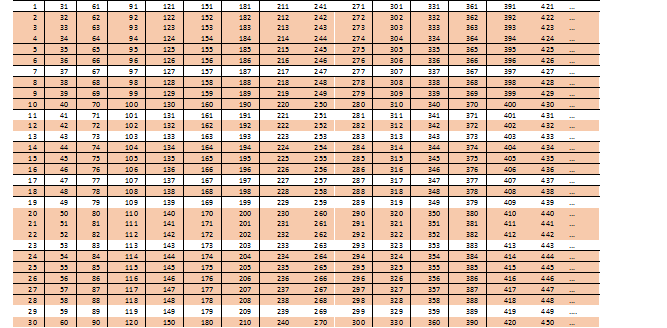
次のことがわかります。

-2n形式の15行、

-3nの形式の5行（2nでは6nの5つのタイプがすでに考慮されています）

-および5nの形式の2行（10nの3つのタイプは、行3nのうち番号2nと15nですでに削除されています）

プライムを含めることはできません（これを期待しましたか？）



30n + iという形式の8行のみが残ります。ここで、i = 1、7、11、13、17、19、23、29です。よく見ると、対称性が確認できます。 1 + 29 = 7 + 23 = 11 + 19 = 13 + 17。



したがって、30n +-iとコンパクトに書くことができます。ここで、i = 1、7、11、13.17です。



そして、任意の素数を見つける確率は8/30以下であることを理解しています。 2/30以下...



次は？ ロジックに従って、次の表には2x3x4x7 = 210行が必要です。 さらに210x11 = 2310、次に2310x13です。したがって、順次素数を乗算して、ラインスキャンのベースをますます大きくし、バンディングを保持します。



素数が「影」を複数の数の無限に投げ込むように見えます。数の底に対応する行に配置されている場合、P（i）で表します。これは素数の連続積iに等しくなります。



素数が含まれる可能性がある最初と次の間にある行のストリップは、非常に単純な法則に従って成長することに気付くことができます：6行、つまり2x3がある場合、素数は5行目にあり、2x3x3であれば、7行目から始まりますそれは論理的です。 したがって、行数30,030（2x3x3x7x11x13）の行列では、最初の行の後に、番号17に続く行までの複合番号の幅広のストリップがあります。いいえ、それは21行目まで伸びます。通常、対称性のため、マトリックスの下部に排他的に化合物番号を持つ20行もあります。

多次元行列と超現実的なフラクタル？

しかし、これらの作品は何ですか？ 2x3は面積が6の長方形です。2x3x5は体積が30の平行六面体です。 2357-4次元のハイパー平行六面体、ハイパーボリューム210 それから？ 5次元、6、...無限大？



素数がすべての次元に影を落とす多次元の世界を想像できると思います...



4次元以上を想像し、平面または3次元空間に投影します。たとえば、多次元ハイパーキューブを一方から他方に転がし、紙で取得した印刷物を見る（およびセクションのフィンガープリントを取得する）ようにマトリックスをレイアウトします。



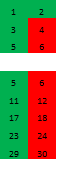
開始行は次のとおりです。







そして、これは2つの側面からのスキャンです。







幸いなことに、右の超平面全体に排他的に合成数があります。 旅行することさえできません。 上から見た別のスキャンを見ることができますが、それからもっと興味深い方向に進みます。







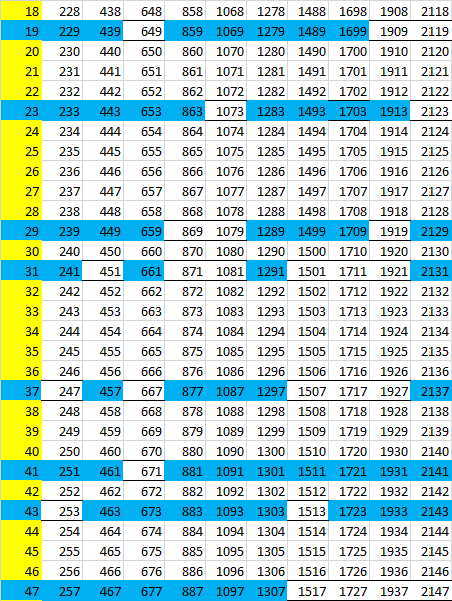
ここで、4番目の次元で、興味のある方向に絵を拡大してみましょう。ここでは素数を見つけることができます。







ここで、茶色の数字はmn形式の数字を表し、11から19（210/11より小さい最も近い整数）の数字の積で構成されています。 これらの数字の特徴は、それら自体が素数ではなく、次の次元の奥深くに「影を落とさない」ことです。



ご覧のように、中央のスイープレイヤーは再び単純になります。以降、素数はありません。 しかし、超平行六面体の外面はさらに検討することができます。 各列は7x11マトリックスに分解され、3x5マトリックスの3つのレイヤーごとに5つのマトリックスを取得します（ここでは、1列のスキャンと2列目のマトリックスのフラグメントを示します）。







スキャンの例についてはこれ以上測定しませんが、記事の枠組み内では不合理です。 記事の最後に、さらにいくつかの図を見ることができます。 この研究があなたの想像力を少し目覚めさせ、あなたがそれが好きであり、複素数と素数の世界に旅するのが有用であることを発見したことを望みます。

おわりに

さらに、著者はこの方法の研究を続けていることに注意したい。 たとえば、3番目、4番目、さらに次の数の積の大きな行列での外観の問題。これにより、深さ投影と体積投影に新しい素数が追加され、両方とも次の次元に影を落とし、残りの「点」斑点が残ります。



しかし、おそらく最も興味深いのは、素数がどんどん見つかる確率の推定値をより洗練させる可能性です。 マトリックスを検討すると、4/6から7/24（または平均11/30）、36/180（または47/210）などの確率がどのように減少するかがわかります。



さらに、著者には分解アルゴリズムがあり、多次元行列での最適化により大幅に加速できます（ただし、分解可能な数の桁数の指数関数的な複雑さはなくなりません）。



基礎となるアルゴリズムは非常に単純です。



pqがXに近くなるように、2つの連続した奇数pとqを使用します（Xが正方形でない場合、ルートをXからより大きなまたはより小さな奇数に丸めます）。 まず、Xのパリティを削除し（結果が偶数になるまで2で除算します）、2 ^ Kの係数を取得します。 次に、ループで、Xとpqの違いを確認します。 ゼロに等しい場合、結果が取得されます。 ゼロより大きい場合、qを2減らします。ゼロより小さい場合、pを2q増やします。 ループでは加算のみが使用されるため、アルゴリズムは非常に高速です（BigIntegerを操作する機能の実装のみに依存します）。



ただし、多重度の基数を使用すると、精度を失うことなく変換ステップを大幅に増やすことができるという著者の仮説があります。 すべての数値Xは2つの連続したP（i）とP（i + 1）の間にあり、P（i）は最初のi個の素数の積であるため、数値Xがどのエッジに近く、pが持つ自由範囲を決定できますq）、したがって同じ平面から形成された長方形pとqは、超平行六面体セクションで展開します。



PSそして、ウィーバーの秘密結社はそれと何の関係があるのか​​、読者は元のタイトルに誰が惹かれたのかと尋ねるでしょうか？ おそらく読者は映画「特に危険」を覚えているだろう。今年は続編を約束している。この映画では、織機が糸と結び目を作ることで予測をしている。



30x7マトリックスの場合：







そして210x11マトリックスの一部：







そして、これらのパンチカードマトリックスは、このマシンの結び目を制御します。 2x3マトリックスによるスキャン：







さらに、6x5マトリックス：