この資料は、このモデルの適用の実際的な側面に専念します。電子およびさまざまな分野の両方で広く使用されていることに注意してください。たとえば、航空および原子力産業のリスク評価、自動車産業の予測、クラウドサービスの信頼性の評価インターネットなどで 繰り返しますが、一般的な仮定は、故障率λは一定であるという仮説です。これは、前の記事で見たように、MTTF = 1 /λに反比例します。
したがって、非常に単純な例から始めましょう。2つの要素で構成され、それぞれの故障率λ1とλ2がわかっているデバイスです。 いずれかの要素が故障すると、デバイス全体が故障します。 たとえば、コンピューターは(条件付きで)プロセッサーとマザーボードで構成されるシステムとして表すことができます。 それらの平均故障時間(MTTF)は2年と3年です(それぞれ、λ1 = 1/2年-1およびλ2 = 1/3年-1 )。 コンピューターの全体的なMTTFスコアはどうなりますか? また、運用開始から1年後にコンピューターが故障する確率はどのくらいですか?
まず、モデルによると、各コンポーネントの故障確率は、
Q 1 (t)= 1-exp(-λ1 t)、
Q 2 (t)= 1-exp(-λ2 t)。
したがって、一般にコンピューターのアップタイムの可能性:
P(t)= [コンピューターのFBG] = [プロセッサーのFBG] * [マザーボードのFBG]、
または、コンピューターの故障率λ(t)に指定されている場合:
exp(-λ(t)t)= exp(-λ1 t)* exp(-λ2 t)= exp(-(λ1 +λ2)t)、
どこから
λ(t)=λ1 +λ2。
つまり システムの故障率は、そのコンポーネントの故障率の合計に等しく 、時間に依存しません(もちろん、指数分布の場合)。
整数の例では、λ= 1/2 + 1/3 = 5/6(年-1 )、MTTF = 1 /λ= 1.2年です。 λがわかれば、一般に、最初の1年間のコンピューター全体の故障の確率を簡単に計算できます。
Q(t = 1年)= 1-exp(-1.2)= 70%、
そして最初の2年間で:
Q(t = 2年)= 1-exp(-2.4)= 91%。
同様に、故障率を単純に合計することにより、より多くのコンポーネントで構成されるシステムのMTTFを計算できます。

繰り返しますが、彼らが言うように、要素のいずれかの障害がシステム全体の障害につながる要素の連続的な (冗長性なしの)接続について話していることを強調します。 この場合、通常、システムはアセンブリに分割され、それぞれのアセンブリについて故障率を計算できます。
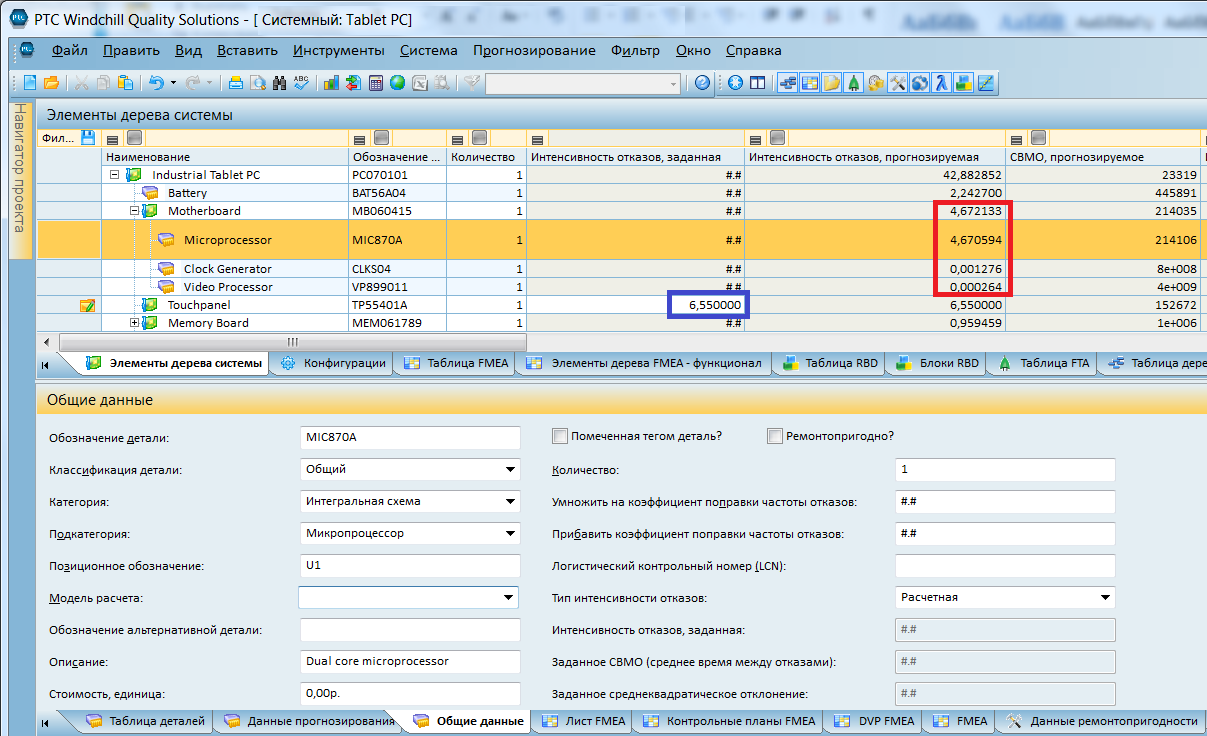
これらのスクリーンショットは、 Windchill Quality Solutions(Relex)の信頼性とリスクを計算するためのプロフェッショナルソフトウェアの使用例を示しています。 実際には、2つの状況が典型的です。
- コンポーネントの場合、既知のMTTF値があります。たとえば、パスポートに示されています(青で強調表示)
- コンポーネントのMTTFは不明です。分類器と参考書に基づいて評価を行う必要があります(スクリーンショットの赤枠)
もう1つの重要な点は、λ特性が動作条件(加熱、放射線被曝、圧力など)に依存することです。 特に、電子部品の場合、温度が上昇すると故障率が増加します。 コンポーネントの信頼性に関するデータは、経済の州やセクターごとに異なる標準によって規制されています。 通常、この情報はリファレンスブックに収集され、対応する補間式の形式で表示されます。たとえば、(抵抗器の場合):

結論として、最も単純なケース、つまり一定の故障率と一貫した回路を考慮したことを改めて指摘します。 次の記事では、コンポーネントの冗長性によりシステムの信頼性を向上させる方法について説明します。