同様の問題を解決するには?
キーと値のペアの数が明らかに少ない場合は、ハードコードするだけで十分です。 しかし、そのような価値が何百万もあるとしたら?
目的のキー値が見つかるまで、リストを簡単に参照できます。 しかし、その場合、複雑さは線形O(N)になり、この場合、エンジニアを混乱させるはずです。 そして、必要なアルゴリズムの複雑さは何ですか? データ量に依存せず、一定の時間で、つまり一定の複雑さO(1)で実行されます。
一定時間のデータを取得するにはどうすればよいですか?
ハッシング
メモリ内のデータを順番に配置し、必要な情報がある場所のオフセットを知っていれば、最初のデータ量に依存しないアクセスを取得できます。
つまり、キーをデータが存在するオフセットに変換する方法を見つける必要があります。 オフセットは単なる整数です:[0、n-1]。ここで、nは保存された値の数です。
ハッシュ関数が助けになります。そのタスクは、キーを整数に正確に変換することです。 このような数値は、データが保存されるオフセットとして解釈できます。
しかし、残念ながら、ハッシュ関数は衝突を引き起こします。つまり、2つの異なるキーが同じオフセットを与える可能性があります。
タスクに基づいて、固定された所定量のデータがあるため、このような問題を回避できます。
完全なハッシング
理想的なハッシュ関数は、既知のキーの静的セットを衝突なしに整数の範囲[0、m-1]に変換するハッシュ関数です。つまり、1つのキーは1つの一意の値にのみ対応します。 そして、結果の値の数が入力キーの数と同じ場合、そのような関数は最小完全ハッシュ関数と呼ばれます。
ランダムグラフに基づく最小の理想的なハッシュ関数の例を考えてみましょう。
各キーが1つの一意のエッジに対応し、それに応じて2つの頂点に対応することを想像してみましょう。
その場合、キーはそのようなプリミティブグラフの形式で表すことができます。

図1.エッジがキーに対応し、2つの頂点で記述されるグラフ。
キーはエッジの形で提示され、エッジは常に(まだハイパーグラフが存在するため)少なくとも2つの頂点を接続するため、目的の関数は次のようになります。
h(キー)= g(ノード1、ノード2)
ここで、 h(key)はエッジを表す最小理想ハッシュ関数、 keyはキー、 g()はグラフnode1およびnode2の頂点に依存する未知の関数です。 キーに依存する必要があるため、判明しました
h(キー)= g(f1(キー)、f2(キー))
実際、 f1とf2では、 1つのキーに使用される任意のハッシュ関数を選択できます。
2つのノードf1(キー)、f2(キー)とエッジの間の関係を記述する未知の関数g()を決定するために残っています。
これがトリックの始まりです
簡単にするために、エッジの値を、このエッジで接続されたノードの値の合計として定義します。
エッジは1つのキーにのみ対応するため、これは望ましい値であり、最小の理想関数の結果です。
h(キー)=(g1(f1(キー))+ g2(f2(キー)))mod m
ここで、 h(キー)はエッジの値、 f1(キー)はグラフの最初のノード、 g1()はこのノードの値、 f2(キー)は2番目のノード、 g2()は2番目のノードの値、 mはエッジの数です。
さらに簡単な場合は、
最小理想関数の値=(ノード1の値+ノード2の値)エッジのmod数。
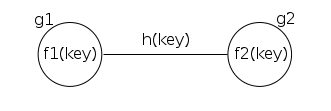
図2.グラフ内の1つのキーの表現。
つまり、ハッシュ関数を使用してノード番号を決定し、多くの場合衝突が発生するため、1つのノードに多くのエッジを含めることができます。
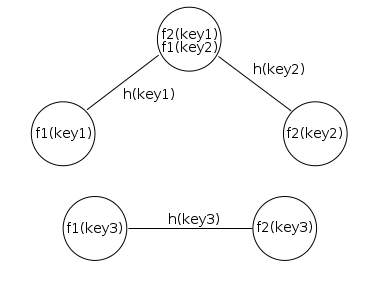
図3.ハッシュ関数の衝突は、1つの頂点に複数のエッジを生成します。 また、あるキーの頂点が別のキーの頂点に接続されない場合があります。
そこに塩があります
グラフのノードがエッジと相互接続される方法を決定したら、まず意図的に一意になるエッジh(キー) (これは単なる増分インデックスです)の値を決定し、次にノードの値を選択します。
たとえば、後続ノードの値は次のように計算できます。
g2(f2(キー))= h(キー)-g1(f1(キー))
または
ノード値2 =エッジ値-ノード1値
グラフを通過するだけで、サブグラフの最初のノードの初期値として0を取り、他のすべてをカウントします。
残念ながら、グラフがループしている場合、このアプローチは機能しません。 グラフがループしないことを事前に保証する方法がないため、ループが検出された場合、他のハッシュ関数でグラフを再描画する必要があります。
ループは、エッジが1つしかない頂点を削除することで最もよく検証されます。 頂点が残っている場合、グラフはループします。
簡単な例
次に、例を使用してアルゴリズム自体を説明します。
タスク:12か月の名前で構成されるキーが多数あります。 最小理想ハッシュ関数を作成する必要があります。この場合、各月は[0、11]の範囲の一意の整数1つだけに変換されます。
1.すべてのキーを調べて、頂点とエッジを追加します。 これを行うには、2つのハッシュ関数f1とf2を選択します。
例:
janキーの場合、最初のノードの番号f1(jan) := 4と2番目のノードの番号f 2(jan) := 13
キーfebの場合、 f1(feb) := 0、f 2(feb) := 17
などなど。
2.グラフがループしているかどうかを確認し、ループしている場合は、手順1を再度繰り返して、関数f1 / f2のハッシュを変更します。
グラフにサイクルが表示される確率は、可能な頂点の数に依存します。 したがって、この概念をグラフサイズ係数として導入します。 ノードの数は次のように定義されます:
m = c * n
ここで、 mはグラフ内のノードの数、 cは一定のサイズ係数、 nはキーの数です。
3.非循環グラフの作成に成功した場合、すべてのノードを調べて、式を使用してそれらの値を計算する必要があります
g2(f2(キー))= h(キー)-g1(f1(キー))
または
子ノード値=エッジインデックス-先祖ノード値
たとえば、ノード番号0を0に割り当て、インデックス6でエッジに沿って進みます。
g2(13)= 6-0 = 6、ノード番号13は値6を取得します。
その結果、このようなグラフができました。
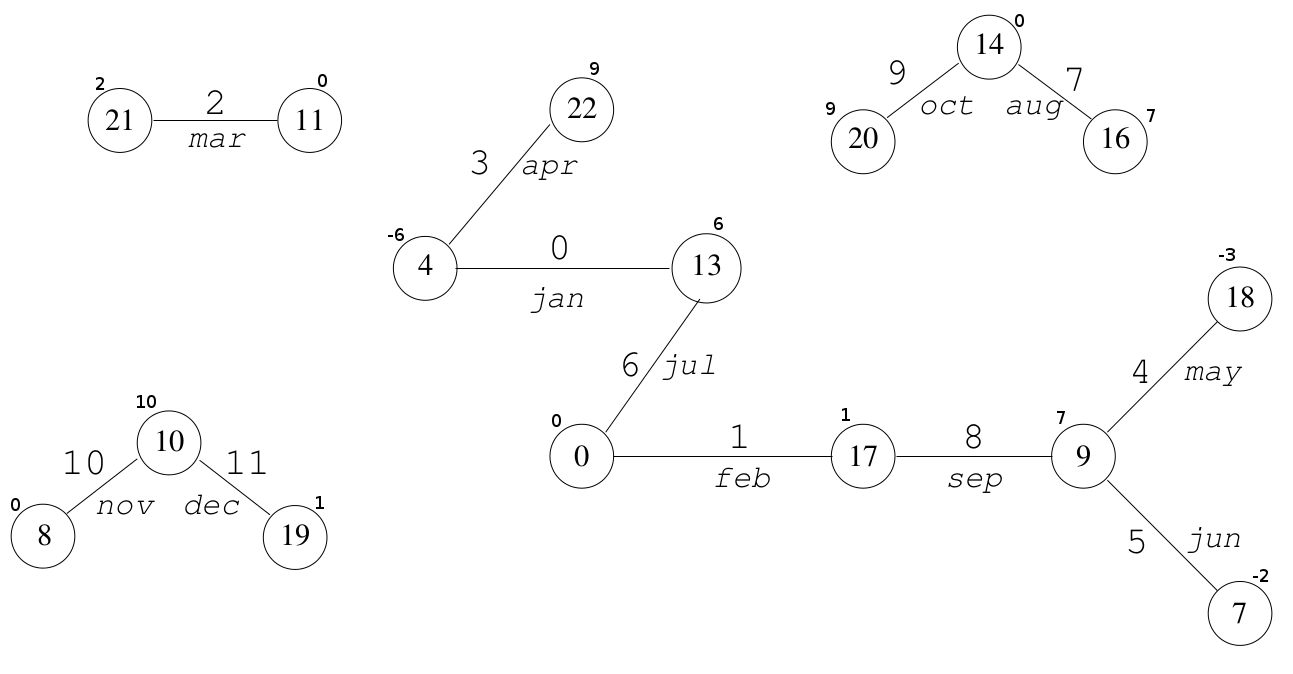
図4.結果のグラフ。月の名前がキーであり、頂点番号を取得するためにランダムハッシュ関数が使用されます。 ノードの近くの数字は、ノードの値です。
ルーキャップ
sepキーの一意のインデックスを取得する必要があるとします。
グラフの作成に使用したものと同じハッシュ関数を使用します。
f1(9月):= 17
f2(9月):= 9
頂点の数を受け取ったら、それらの値を追加します。
h(sep)=(g(17)+ g(9))mod 12 =(1 + 7)mod 12 = 8
このアルゴリズムはCHMと呼ばれ、 CMPHライブラリに実装されています。
ご覧のとおり、ハッシュテーブルの作成には線形複雑度O(N)があり、キーによるインデックス検索は定数O(1)です。
あとがき
Googleのひげを生やしたパズルを覚えていますか?
リストノードが次のように見える場合、線形時間で単方向リストをコピーする方法は?
struct list_node
{
list_node * next;
list_node *ランダム。
};
そして、ソリューションはノードのクローンを作成してノードの2つのコピーが連続するようにし、ノードのコピーを含むこのリストをそれぞれコピーのある2つのリストに分割します。 その結果、複雑さは直線的です。
ここで、ポインターでリストにインデックスを保存し、インデックスでポインターを保存できる最小の理想的なハッシュ関数を想像してください。 そして、次のような問題を解決することが可能になります。
1.リストを調べて、ノードポインターの配列とそのインデックスを取得します。
2.ノードポインターの最小限の理想的なハッシュ関数を作成します。
3.新しいリストを作成し、ノードインデックスとそのポインターの配列を取得します。
4.インデックスでアドレスを取得するために、2番目のリストのインデックス用に他の理想的な関数を作成します。
5.新しいリストを調べ、古いノードのアドレスを取得し、そこからインデックスを取得し、2番目のハッシュ関数から、インデックスによって2番目のリストに既にあるアドレスを取得します。
その結果、リストは線形時間でコピーされます。
もちろん、アイデアはノードを複製し、2つのリストに分割し、より美しく、より速くすることです。
努力してくれてありがとう。
読む
1. ZJチェコ、G。ハバス、およびBSマジェウスキ。 最小限の完全なハッシュ関数を生成するための最適なアルゴリズム、情報処理文字、43(5):257-264、1992。
2. 最小限の完全ハッシュ関数-はじめに 。
3. mphf -C ++でのCHMの実装。