はじめに
日曜日の早朝、3日目、私はレーザースキャンの結果を三角測量するためのプログラムのデバッグに座っていました。 レーザースキャンは、3次元のポイントのセットです。 プログラムの結果として、ポイントを結合してポリゴンを切り離し、サーフェスモデルを作成する必要があります。 一枚の紙の上で機能ごとに機能を振り返り、最後に、ドローネ条件が満たされていることを確認する機能に到達しました。 どうやら、エラーがどこかに潜んでいたようです。 詳細な分析の結果、ドローネの三角形分割に関する膨大な数の本に示されている式が、常に正しい結果を与えるとは限らないことが判明しました。 カットの下の詳細。
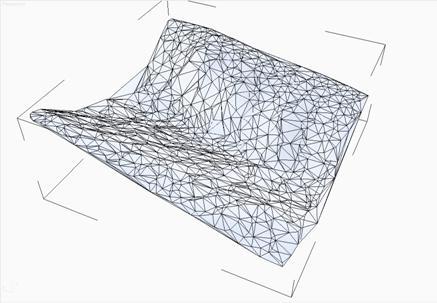
ドローネ条件
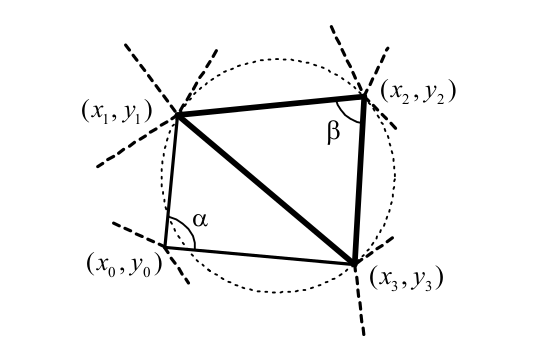
ドローネの状態自体について簡単に説明します。 ところで、A.V。のすばらしい本からすべての情報を得ました。 Skvortsova 「ドロネー三角形分割とその応用」 与えられた三角形分割点のいずれも、構築された三角形の外接円内に収まらない場合、三角形分割はドローネ条件を満たしていると言われています。 すべての三角形分割三角形の最小角度の合計を最大化するには、この条件が満たされる必要があります。 簡単に言えば、三角形が平らにならないようにするためです。
著者は、ドローネの状態をチェックする2つの方法を提供し、それぞれの最適化の可能性を示しています。
最初の方法は最も明白です。 彼は、外接円の中心と半径を計算し、隣接する三角形の頂点の所属を直接確認することを提案しています。 最適化として、計算された外接円を三角形のクラスに保存することが提案されています。 最適化されていない検証には、29の乗算と除算の演算と24の加算と減算の演算が必要です。 最適化されたチェックの複雑さは、三角形分割アルゴリズムに依存します。
2番目の方法はすでに興味深いものです。 彼は、条件を検証するために、隣接する三角形については、反対の角度の合計がPI(
 )、これは条件と同等です:
)、これは条件と同等です:  。
。
さらに、ゴーストと変換の後、かなり怖い式が得られます:
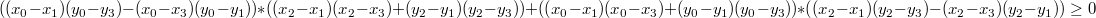
式は合計のサインに対応します。
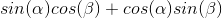 ここで、余弦と正弦は、それぞれスカラー積と擬似スカラー積の式で表されます。 式では、ベクトルの長さの積は省略されます(明らかに式の符号に影響しないため)。
ここで、余弦と正弦は、それぞれスカラー積と擬似スカラー積の式で表されます。 式では、ベクトルの長さの積は省略されます(明らかに式の符号に影響しないため)。
最適化として、最初に余弦符号を計算することが提案されています。 もし
 そして
そして 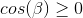 意味する
意味する 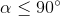 そして
そして  つまり ドローネ条件が満たされます。 もし
つまり ドローネ条件が満たされます。 もし  そして
そして  意味する
意味する 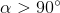 そして
そして  、条件は満たされていません。 それ以外の場合は、完全な式を確認する必要があります。
、条件は満たされていません。 それ以外の場合は、完全な式を確認する必要があります。
完全な条件による検証には、10回の乗算/除算と13回の加算/減算が必要です。 本の著者によると、最適化されたチェックには、乗算/除算の約7つの操作と加算/減算の9つの操作が必要です。
この情報を確認した後、私は後者の方法が他の方法よりも最適であるという論理的な結論を下し、それを使い始めました。 彼らが言うように、トラブルの前兆はありませんでした。
落とし穴
デバッグ中に、ドローネ条件をチェックするための関数の不適切な動作に気付き始めました。 問題は、サインのサインが頂点をリストする順序に依存することであることが判明しました。 したがって、サイン記号のため、式全体の記号が変わります。 何か分からないかもしれませんが、誰かが私を修正してくれたら嬉しいです。
発生した状況を修正する最初の唯一の方法は、サイン式をモジュロを取ることです。 したがって、サインは角度の大きさのみを示し、スイープの方向は示しません。これは、私たちにとって有利です。
おわりに
この式が膨大な数の本で示されていることは、私にとって非常に驚くべきことです。 ロシア語の文献だけでなく、同じ情報が記載されている出版物もあります。
私は数学の専門家ではないので、コミュニティから十分な批判と提案を期待しています。 議論の準備ができています。
ご清聴ありがとうございました。