圧縮画像品質基準
非可逆圧縮アルゴリズムについて話す前に、許容可能な損失と見なされるものについて同意する必要があります。 主な基準が画像の視覚的評価のままであることは明らかですが、圧縮画像の変化も定量化できます。 評価する最も簡単な方法は、圧縮されたイメージとソースイメージの直接の差を計算することです。 私たちはそれに同意します
元の画像のi番目の行とj番目の列の交点にあるピクセルを理解します。 
-圧縮画像の対応するピクセル。 その後、任意のピクセルについて、コーディングエラーを簡単に判断できます 
、およびN行M列で構成される画像全体について、合計誤差を計算できます 
。 明らかに、総誤差が大きいほど、圧縮画像の歪みが強くなります。 それにもかかわらず、この値は実際にはめったに使用されません。 画像のサイズは考慮されません。 はるかに広い標準偏差を使用した推定 
。
別の（本質的には近い）アプローチは次のとおりです。最終画像のピクセルは、元の画像のピクセルとノイズの合計と見なされます。 このアプローチの品質基準は、S / N比（SNR）と呼ばれ、次のように計算されます。
。
これらの評価は両方とも呼ばれます 生殖の忠実度の客観的基準、なぜなら 元の圧縮画像のみに依存します。 ただし、これらの基準は常に主観的な評価に対応するとは限りません。 画像が人間の知覚を目的としている場合、唯一言えることは、客観的基準の貧弱な指標はほとんどの場合主観的評価の低下に対応しますが、客観的基準の良好な指標は高い主観的評価を保証しません。
量子化とサンプル圧縮
視覚的冗長性の概念は、量子化と離散化のプロセスに関連付けられています。 画像内の情報の大部分は、人間には知覚されません。たとえば、人間は明るさのわずかな違いに気づくことができますが、色にはあまり敏感ではありません。 また、特定のポイントから開始して、サンプリングの精度を上げても、画像の視覚的な認識には影響しません。 したがって、視覚的な品質を損なうことなく情報の一部を削除できます。 このような情報は視覚的に冗長と呼ばれます。
視覚的な冗長性を除去する最も簡単な方法は、サンプリングの精度を下げることですが、実際には、この方法は単純な構造の画像にしか適用できません。 複雑な画像で生じる歪みは目立ちすぎます（表1を参照）
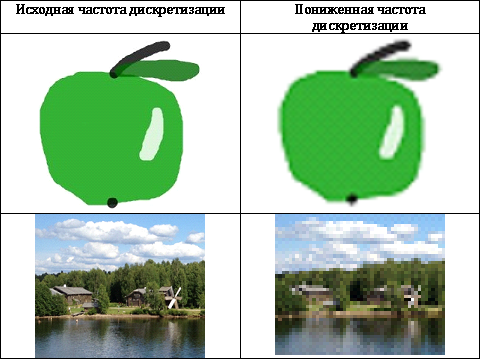
冗長な情報を削除するために、量子化の精度が低下することがよくありますが、それは軽率に低下することはありません これにより、画質が急激に低下します。
すでに知っている画像を考えてください。 画像がRGB色空間で表されると仮定すると、量子化精度が低下したこの画像のエンコード結果が表に示されています。 2。
考慮された例では、均一量子化が最も簡単な方法として使用されますが、色再現を維持することがより重要な場合は、均一量子化を使用しますが、セグメントの中央ではなく、このセグメントの輝度の数学的期待値を選択するか、または明るさの範囲全体の不均等な分割を使用します。
受信した画像を入念に調べたところ、圧縮された画像に独特の偽輪郭が現れ、視覚を著しく悪化させることがわかります。 次のピクセルへの量子化誤差の転送に基づいた方法があり、これらの輪郭を大幅に削減または完全に削除することもできますが、画像ノイズと粒子の外観につながります。 これらの欠点は、画像圧縮のための量子化の直接使用を大幅に制限します。
視覚的に冗長な情報を削除する最新の方法は、人間の視覚の特徴に関する情報を使用します。 誰もが、画像の色と明るさに関する情報に対する人間の目の感度の違いを知っています。 タブで。 図3は、色差信号IQの異なる量子化深度でエンコードされたYIQ色空間の画像を示しています。
表からわかるように。 図３に示されるように、色差信号の量子化深度は、視覚的変化を最小限に抑えながら２５６から３２レベルに低減することができる。 同時に、IおよびQ成分の損失は非常に大きく、表に示されています。 4
説明した方法は単純ですが、純粋な形ではほとんど使用されず、ほとんどの場合、より効率的なアルゴリズムのステップの1つとして機能します。
予測コーディング
予測コーディングは、非常に効率的な可逆情報圧縮技術としてすでに見ています。 コーディングと量子化による予測および圧縮を組み合わせると、非常にシンプルで効率的な非可逆画像圧縮アルゴリズムが得られます。 検討中の方法では、予測誤差は量子化されます。 圧縮の程度と、圧縮画像に導入される歪みの両方を決定するのは、量子化の精度です。 予測と量子化に最適なアルゴリズムを選択することは、かなり難しい作業です。 実際には、次の汎用（ほとんどの画像で許容可能な品質を提供する）予測子が広く使用されています。
次に、損失を伴うコーディングの最も単純な方法であると同時に非常に一般的な方法を詳細に調べます。 デルタ変調。 このアルゴリズムは、前の1つのピクセルに基づく予測を使用します。
。 予測段階後に得られる誤差は、次のように量子化されます。
一見、これは量子化の非常に粗雑な方法ですが、1つの紛れもない利点があります。予測結果を1ビットでエンコードできることです。 タブで。 図5は、さまざまなξ値を持つデルタ変調（ラインごとのトラバーサル）を使用してエンコードされた画像を示しています。
2つのタイプの歪みが最も顕著です-輪郭のぼやけと画像の特定の粒状性。 これらは、急勾配の過負荷と、いわゆる ノイズ粒度。 このような歪みは、すべての損失のある予測コーディングオプションで一般的ですが、最もよく見られるのはデルタ変調の例です。
粒度ノイズは、主にモノフォニック領域で発生します。ξの値が、明るさの小さな変動を正しく表示するには大きすぎる場合（または存在しない場合）。 図 1、黄色の線は初期輝度を示し、青色の列は予測誤差を量子化するときに発生するノイズを示します。
勾配の過負荷状況は、粒度ノイズのある状況と根本的に異なります。 この場合、量ξは明るさが急激に異なるため、小さすぎます。 エンコードされた画像の明るさは元の画像の明るさほど速く成長できないという事実により、輪郭の顕著なぼやけがあります。 急勾配による過負荷の状況は、図で説明されています。 2
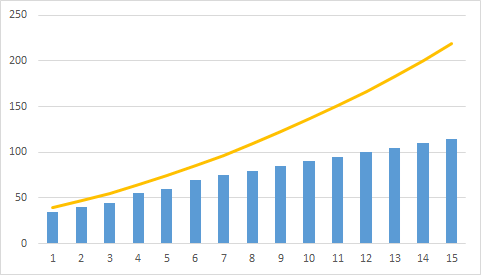
粒度のノイズがξの減少とともに減少することは容易にわかりますが、これに伴い、急峻性に沿った過負荷により歪みが増加し、逆もまた同様です。 これにより、ξを最適化する必要が生じます。 ほとんどの画像では、ξ∈[5; 7]を選択することをお勧めします。
変換コーディング
前に説明したすべての画像圧縮方法は、元の画像のピクセルに直接作用しました。 このアプローチは空間コーディングと呼ばれます。 現在のセクションでは、変換コーディングと呼ばれる根本的に異なるアプローチを検討します。
このアプローチの主な考え方は、先に検討した量子化を使用した圧縮方法に似ていますが、ピクセルの輝度は量子化されませんが、変換係数（変換係数）はそれらに基づいて特別に計算されます。 変換圧縮と画像復元のスキームを図に示します。 3、図 4。
直接圧縮はエンコードの時点では発生しませんが、係数の量子化の時点で発生します。 ほとんどの実際の画像では、ほとんどの係数を大まかに量子化できます。
係数を取得するには、可逆線形変換を使用します。たとえば、フーリエ変換、離散コサイン変換、ウォルシュアダマール変換などです。 特定の変換の選択は、許容される歪みのレベルと利用可能なリソースに依存します。
一般的な場合、N * Nピクセルの画像は2つの引数I（r、c）の離散関数と見なされ、直接変換は次のように表現できます。
セット
これは正確に望ましい係数のセットです。 このセットに基づいて、逆変換を使用して元の画像を復元できます。
機能
は変換カーネルと呼ばれ、関数gは直接変換のカーネルであり、関数hは逆変換のカーネルです。 変換コアの選択により、変換の実行に必要な圧縮効率とコンピューティングリソースの両方が決まります。
広範な変換カーネル
変換コーディングで最もよく使用されるのは、以下にリストされているカーネルです。
これらのコアの最初の2つのコアを使用すると、離散フーリエ変換の簡素化されたバージョンが得られます。 核の2番目のペアは、非常に頻繁に使用されるウォルシュアダマール変換に対応します。 最後に、最も一般的な変換は離散コサイン変換です。
広範囲の離散コサイン変換は、画像エネルギーを圧縮する能力が優れているためです。 厳密に言えば、より効率的な変換があります。 たとえば、Karhunen-Loev変換は、エネルギー圧縮に関しては最高の効率を発揮しますが、その複雑さにより、実際に幅広い実用化の可能性が排除されます。
エネルギーの高密度化効率と実装の比較容易さにより、離散コサイン変換が変換コーディングの標準になりました。
変換コーディングのグラフィカルな説明
機能分析のコンテキストでは、考慮される変換は、基底関数のセットの拡張と見なすことができます。 同時に、画像処理のコンテキストでは、これらの変換は基本的な画像への分解として認識できます。 この考えを明確にするために、サイズn * nピクセルの正方形の画像Iを考えます。 変換カーネルは、変換係数または元の画像のピクセル値に依存しないため、逆変換は行列形式で記述できます。
これらの行列が正方形の形で配置され、得られた値が特定の色のピクセルの形で提示される場合、基底関数のグラフィカルな表現を得ることができます。 基本的な画像。 n = 4のウォルシュアダマール変換と離散コサイン変換の基本的な画像を表に示します。 7。
変換コーディングの実用的な実装の特徴
変換コーディングの一般的な考え方は前に説明しましたが、それでも、変換コーディングの実用的な実装にはいくつかの問題の明確化が必要です。
エンコードする前に、画像は正方形のブロックに分割され、各ブロックが変換されます。 計算の複雑さと最終的な圧縮効率は、ブロックサイズの選択に依存します。 ブロックサイズが大きくなると、圧縮効率と計算の複雑さが増すため、実際には8 * 8または16 * 16ピクセルのブロックが最もよく使用されます。
各ブロックの変換係数が計算された後、それらを量子化およびエンコードする必要があります。 最も一般的なアプローチは、ゾーンとしきい値のコーディングです。
ゾーンアプローチでは、最も有益な係数が結果の配列のゼロインデックスの近くにあると想定されます。 これは、対応する係数を最も正確に量子化する必要があることを意味します。 他の係数は、より粗く量子化するか、単に破棄することができます。 ゾーンコーディングの概念を理解する最も簡単な方法は、適切なマスクを見ることです（表8）。
セル内の数字は、対応する係数をエンコードするために割り当てられたビット数を示します。
同じマスクが任意のブロックに使用されるゾーンコーディングとは異なり、しきい値コーディングは各ブロックに一意のマスクを使用することを意味します。 ブロックのしきい値マスクは、次の考慮事項に基づいて構築されます：元の画像を復元するための最も重要な要素は、最大値の係数です。したがって、これらの係数を保持し、他のすべてをゼロにすることで、復元された画像の高い圧縮率と許容可能な品質の両方を確保できます。 タブで。 図９は、特定のブロックの例示的なマスクビューを示している。
単位は格納および量子化される係数に対応し、ゼロは放出された係数に対応します。マスクを適用した後、結果の係数行列は1次元配列に変換する必要があり、変換にはスネークトラバーサルを使用する必要があります。 次に、結果の1次元配列では、すべての重要な係数が前半に集中し、後半はほぼ完全にゼロで構成されます。 前に示したように、このようなシーケンスは、シリーズ長のコーディングアルゴリズムによって非常に効率的に圧縮されます。
ウェーブレット圧縮
ウェーブレットは、データの周波数成分を分析するために設計された数学関数です。 ウェーブレットは情報圧縮の問題で比較的最近使用されていますが、それでも研究者は素晴らしい結果を達成することができました。
上記で説明した変換とは異なり、ウェーブレットでは、元の画像をブロックに予備分割する必要はありませんが、画像全体に適用できます。 このセクションでは、例としてかなり単純なHaarウェーブレットを使用して、ウェーブレット圧縮について説明します。
最初に、1次元信号のHaar変換を考えます。 n個の値のセットSがあるとします。Haar変換中に、2つの数値が要素の各ペアに割り当てられます。要素の半和とその差です。 この変換は可逆的であることに注意することが重要です：すなわち 数字のペアから、元のペアを簡単に復元できます。 図 図5は、1次元Haar変換の例を示しています。
信号は2つのコンポーネントに分割されることがわかります。元の近似値（解像度が半分に低下）と明確な情報です。
2次元Haar変換は、1次元変換の単純な構成です。 ソースデータがマトリックスの形式で表示される場合、変換は最初に各行に対して実行され、次に各列の変換が結果のマトリックスに対して実行されます。 図 図6は、2次元Haar変換の例を示しています。
色は、ポイントでの関数の値に比例します（値が大きいほど暗くなります）。 変換の結果、4つのマトリックスが取得されます。1つは元の画像の近似値（サンプリング周波数を下げた）を含み、他の3つは明確な情報を含みます。
圧縮は、リファインメント行列からいくつかの係数を削除することにより実現されます。 図 図7は、リファインメント行列から小さなモジュロ係数を除去した後の回復プロセスと再構成画像自体を示しています。
明らかに、ウェーブレットを使用した画像の表現により、画像の視覚的な品質を維持しながら、効果的な圧縮を実現できます。 その単純さにもかかわらず、Haar変換は実際には比較的まれにしか使用されません。 いくつかの利点がある他のウェーブレット（Daubechiesウェーブレットまたは双直交ウェーブレットなど）があります。
PSモノグラフの他の章はgorkoff.ruから無料でアクセスできます。