私を信じて、それは簡単ではありませんでした。 それらは理解できますが。
ご存知のように、タスクの条件の準備は、プログラミング競技の準備で最も難しい段階の1つと見なされます。
通常、これらはトレーニングチームや外部コンテストで使用されます。
さまざまな大学のトレーナーのチームが定期的にコンテストを交換しています。
一般的に、オリンピアード運動ではタスクの再利用が認められています。

しかし、まず最初に。
オリンピアードの通信ラウンドで成功裏に演じたロシアとベラルーシ共和国のさまざまな地域からの8から11クラスの70人以上の学童が、オリンピアードの対面ラウンドに参加するよう招待されました。
イベントの形式には2つの段階が含まれることを思い出してください。 。
主催者は、モスクワとサンクトペテルブルクの専門学校の天才やオタクに依存していないことに注意しています。
オリンピアードの目的は、主にロシアや近隣諸国から、良い教育を受けて情報技術の分野で自分自身を実現したい有望で才能のある人を探すことです。
工学 2年目から、 工学サイバネティックス学部の学生は大学の研究所でインターンシップを受け、彼らのベストはCognitive Technologiesと共同で実装されたAIの分野で実際の科学および応用プロジェクトに参加するように招待されます。
オリンピアードのフルタイムのラウンドは、次のルールに従って開催されました。
- ツアーの期間: 5時間 。
- タスク数: 10
- 使用言語: ロシア語 。
参加者をランク付けして勝者を特定する際の主な要因は、解決されたタスクの数です。
それらが等しい場合、トーナメントの開始から、解決されたすべての問題に関する決定のチェックシステムによる採用までの時間の合計に、拒否された決定ごとに20分のペナルティが考慮されました。
誤った決定に対するペナルティは、検証システムによって最終的に受け入れられたタスクにのみ課されました。
ソリューションの自動検証には、ejudgeシステム( https://ejudge.ru/ )が使用されました。
その結果、10個の問題を解決した人はいませんでした。
オリンピアードの勝者は、9つの問題を解決した、ベラルーシ共和国のイビエフ中等学校の国際情報オリンピックアレクセイヴィシュヤズの銀メダリストでした。
彼から目立ったマージン(5つの解決された問題)で、 アレクサンダー・ゾイキン (オレンブルク)とユーリ・ボンダルチュク (ベラルーシ)は2位を共有しました。
Pavel Beschetnov (Tolyati)、 Dmitry Galov (Moscow)、およびAleksey Dovgal (Belarus)は、4つのタスクを解決して3位でした。
受賞者および受賞者として認められた16人の学童は、NUST「MISiS」への入学時に試験の全体的な結果に貴重な賞品と追加ポイントを与えられました。
最も困難なのは、タスクIの「廊下の鏡」です。
驚くべきことに、参加者はジオメトリの問題をうまく処理できませんでした。
主催者はそれらを比較的単純であると考えました。
タスクIテキスト
制限時間: 0.5秒
メモリ制限: 64メガバイト
入力: 標準入力ストリーム(stdin)
出力: 標準出力ストリーム(stdout)
誰かが突然ドアを開けたとき、冷たいペティアはベッドに横たわっていました。 ペティアは怠けすぎて立ち上がることができず、鏡を見ながら誰が来たのかを確認しました。 入る人の座標はわかっており(重要なポイントと考えることができます)、ピートが鏡に入る人の反射を見ることができるかどうかを調べる必要があります。 ミラーは原点を中心とする円の形をしており、平面ax + by + cz = 0にあります。Petyaも重要なポイントと見なすことができます。 ペティアと見知らぬ人が鏡の平面に横たわることがなく、ペティアが常に鏡の反射面を見ることが保証されています。 画像が鏡の縁に当たると、Petyaは人が入っているのを確認します。 Petyaと入る人の両方が重要なポイントと見なされるため、Petyaは入る人と自分の反射の両方を通して入る人の反射を見ることができます。
ソースデータ
最初の行には正の整数n -500を超えないテストの数が含まれます。各テストは4行で構成されます。 それらの最初は、ミラーの半径を含んでいます。 2番目-係数a 、 b 、 c 。 プチの座標が続きます。 各テストの4行目には、入力した人の座標が含まれています。 すべての数値は整数であり、絶対値で1000を超えません。
結果
n行を印刷します。 各行には、次のテストへの答えがあります。 Petyaが人の入室を確認した場合は「はい」、そうでない場合は「いいえ」。
例
| ソースデータ | 結果 |
|---|---|
| 2
2 0 1 0 0 2 0 0 1 0 1 0 1 0 2-2 0 1 1 0 | はい
いや |
タスクI「廊下の鏡」の分析
鏡の平面に対してペティアを反射します。
反射したペティアと見知らぬ人を通る直線を描き、それを鏡の平面と交差させます。 交点がミラーに当たるかどうかを見てみましょう。 ペティアと見知らぬ人が鏡の反対側に横たわっている場合を個別に検討します-ペティアは間違いなく彼を見ません。

問題Hのテキスト「対称軸」
制限時間: 1秒
メモリ制限: 64メガバイト
入力: 標準入力ストリーム(stdin)
出力: 標準出力ストリーム(stdout)
友人はChinaを作るためのキットをChina Vovaへの旅行から持ってきました。
翌日は天気が良かったので、彼はヘビを接着して走らせることにしました。
製造指示書はもちろん中国語でしか書かれていなかったため、Vovaはそれを使わずにそれを理解することにしました。
少しいじって、彼は平らな多角形の形をした蛇を作りました。残ったのはそれに尾を刺すことだけでした。
そして、Vovaはヘビの尻尾をどのポイントに接着するかを考えなければなりませんでした。
直感は、ヘビの飛行が安定するためには、その尾が多角形の対称軸にあるべきだと彼に言いました。
以下の図は、安定して飛行する2つのflyingと、それらに尾を付けるためのすべてのオプションを示しています。
不規則にflyingが飛んでいます。
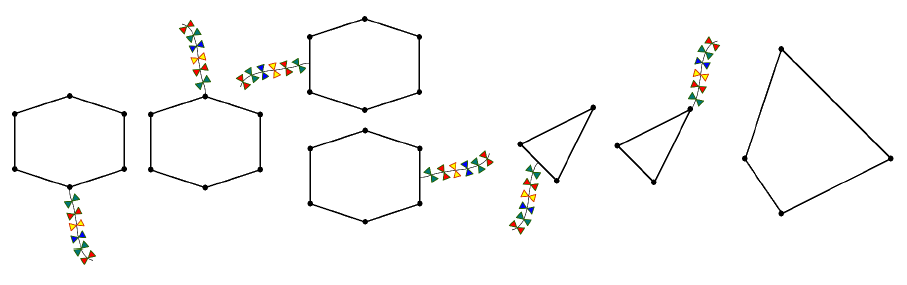
ポリゴンの境界上にいくつのポイントが存在し、尾をそれらに貼り付けた場合、カイトが安定して飛行しますか?
ソースデータ
最初の行には、単一の整数N (3≤N≤1000)が含まれています。 次のN行には、絶対値で10000を超えない2つのスペースで区切られた整数が含まれます。これは、走査順序でのポリゴンの頂点の座標です。
結果
単一の数字を印刷します-ヘビの尾を貼り付けることができるポリゴンの境界上のポイントの数。
例
| ソースデータ | 結果 |
|---|---|
| 6
3 3 6 2 6 -1 3 -2 0 -1 0 2 | 4 |
| 3
-2 2 2 4 0 0 | 2 |
| 4
0 6 6 0 0 -3 -2 0 | 0 |
問題Hの分析「対称軸」
ポリゴンの対称軸は、頂点と側面の中間点のみを通過できます。
2Nポイントの座標(ポリゴンの頂点とその辺の中点)を走査順に書き留め、 0から2N-1までの番号を付けます。
対称軸のすべての候補、つまり点iとi + Nを通る線、0≤i≤N -1を考えます。
そのような線が多角形の対称軸になるためには、点i + jおよび(ij)mod 2Nの各ペア、 1≤j≤N-1がこの線に対して対称に配置されていることが必要かつ十分です。
線ABに関して点CとDの位置の対称性をチェックする最も簡単な方法は、線ABとCDが直交し、それらの交点がセグメントCDを半分に分割することを確立することです。
整数による計算を超えないようにするには、ポイントのすべての座標を4倍にするだけで十分です。
このようなソリューションの複雑さはO(N 2 )です。
2人の参加者A. VistyazhとP. Beschetnovは 、タスクH「対称軸」に対処しました。
冬の学校
フルタイムツアー中に、冬のプログラミングスクールも子供向けに開催されました。
その枠組みの中で、有名な科学者とIT専門家がオリンピアードの参加者に講義を行い、マスタークラスと教育コンテストを開催しました。
ウィンタースクールへの参加とプログラミングオリンピアードの対面ツアーは、招待された参加者に対して無料で行われました。 送迎、食事、宿泊施設が提供されました。
各参加者は駅で待ち合わせ、会場に案内されました。 滞在中、プロのカウンセラーは小学生と協力し、旅行会社OST-WESTが主催するカウンセラー学校で訓練を受けました。
オリンピアードのフルタイムラウンドのタスクとテストは、対応するメンバーが率いるNUST「MISiS」とCognitive Technologiesのスポーツプログラミングのトレーナーチームによって開発されました。 RAS V.L. アラザロフ。 その中で:博士号 I.A. ファラエフ博士 V.V. ポストニコフ博士 I.B. ママイ、V.V。 ソコロフ。 NUST「MISiS」の大学院生だけでなく、K。Bulatov、T。Chernov、N。Skoryukina。