
これは、「鉄道」のリクエストでGoogleで見つかった完全に普通の写真です。 そして、道路自体も同様です。
この写真を削除して、メモリから鉄道を引くように頼むとどうなりますか?
あなたが7歳くらいの子供で、前に絵を描くことを学んだことがない場合、次のようなものを手に入れることになるでしょう。
おっと 何かが間違っているようです。
1.物事を見る奇妙な方法
最初の写真のレールに戻って、何が間違っているのかを理解してみましょう。
実際、長い間見ていると、周囲の世界を正確に反映していないことが明らかになります。 私たちがすぐにつまずいた主な問題は、たとえば、平行線がそこで交差することです。 一連の同一の(実際には)街灯柱は、実際には次の柱が次第に小さくなるように描かれています。 道路の周りの木々は、最初は明確な枝と葉を持っていますが、無地の背景に融合し、さらに何らかの理由で明確な紫色の色合いを獲得します。
これらはすべて遠近効果であり、3次元のオブジェクトが目の内側の2次元の網膜に外部から投影されるという事実の結果です。 これについて魔法のようなことは何もありません-おそらく、これらの輪郭と線の歪みが空間の向きに問題を引き起こさないのは少し不思議ですが、鉛筆を握ろうとすると突然脳が緊張します。
別の素晴らしい例は、幼い子供たちが空を描く方法です。

空は上にあるはずです-ここでは、青い帯が上端に固定されています。 シートの中央は白のままで、太陽が泳ぐ空間で満たされています。
そして、これはいつでもどこでも起こります。 立方体は正方形の面で構成されていることがわかっていますが、 写真を見ると、そこに単一の直角は表示されません。さらに、これらの角度は絶えず変化しているため、表示角度を変更する価値があります。 まるで頭の中のどこかに、通常の3次元オブジェクトの大まかな輪郭があるように見えます。そして、結果を自分の目で見たものとすぐに比較する時間がないので、レールを描くプロセスを回します。
実際はもっと悪いです たとえば、道路の最初の写真で、道路のどの部分が近くにあり、どの部分がより遠くにあるかをどのように判断しますか? オブジェクトの削除が小さくなると、OK-しかし、誰かが連続して減少する寝台を次々と隠して置くことによってあなたをだましていないと確信していますか? 遠くの物体は通常、青みがかった青みがかった色(「大気遠近法」と呼ばれる効果)ですが、被写体は単純にそのような色で塗ることができ、そうでなければ完全に正常に見えます。 ここからほとんど見えない鉄道を渡る橋は、ライト(オクルージョン効果)によって隠されているため、私たちの背後にあるように見えます-しかし、再び、どのようにライトが単にその表面に描かれていないことを確認できますか? シーンの3次元性を評価するためのこの一連のルールは、主にあなたの経験に依存します。おそらく、光と平坦な地平線から落ちて、大気中で生き残るために訓練された先祖の遺伝的経験に依存します。
この視覚的経験に満ちた強力な分析プログラムの助けがなければ、それ自体では、写真は周囲の世界についてほとんど語りません。 画像は、ほとんどの場合、すでに記憶にあるシーンを心に想像させるトリガーになる可能性が高くなります。 それらには実際のオブジェクトは含まれていません-それらについての限られた、平坦化された、悲劇的な二次元のアイデアのみであり、さらにそれは動きとともに絶えず変化しています。 ある意味では、私たちはフラットランドの住人であり、片側だけで世界を見ることができ、必然的に歪曲されています。
より多くの視点
一般に、周囲の世界は、視点がすべてを歪める方法の証拠でいっぱいです。 ピサの斜塔を支える人々、太陽を手にした写真、エッシャーの古典的な絵画は言うまでもなく、ここに完璧な例があります- エームスルーム 。 これらは、欺くために特別に作られた孤立したトリックではないことを理解することが重要です。 パースペクティブは常に劣った画像を示しますが、原則として、それを「デコード」することができます。 窓の外を見て、あなたが見るものは欺き、ゆがみ、絶望的な劣等だと考えてみてください。
2.画像は本物ではありません、Neo
あなたがニューラルネットワークだと想像してください。
それほど難しいことではありません-結局のところ、どういうわけか本当にそうです。 パスポートオフィスで書類の顔を認識する自由な時間を過ごします。 あなたは非常に優れたニューラルネットワークであり、作業はそれほど複雑ではありません。プロセスでは、人間の顔に厳密に特徴的なパターン(両目、鼻、口の相互配置)に導かれるからです。 目と鼻自体は異なる場合があります。写真の兆候の1つは区別できない場合がありますが、他の人の存在が常に役立ちます。 そして突然あなたはこれに出くわします:

うーん、あなたは思う。 あなたは間違いなくおなじみの何かを見る-少なくとも中央には、1つの目があるようだ。 確かに、奇妙な形-それは三角形のように見え、先の尖った楕円のようではありません。 2番目の目は見えません。 鼻は真ん中と目の間にあるはずですが、輪郭の端まで完全に行きましたが、口がまったく見つかりませんでした-間違いなく、左下の暗い角は彼のようには見えません。 顔ではない-あなたが決定し、ゴミ箱に写真を投げます。
ですから、私たちの視覚システムが画像のパターンの単純な比較に従事していたと思います。 幸いなことに、彼女は何らかの形で違った考え方をしています。 私たちは、顔が顔のように少なくならないようにする第2の目がないことを心配していません。 私たちは、2番目の目が反対側にあるべきであると精神的にふりをし、その形状は、写真の頭が向きを変えて側を向いているという事実だけに起因します。 言葉で説明しようとするとき、些細なことは不可能に思えますが、完全に反対する人もいます。
最も厄介なのは、この問題を機械的に解決する方法が見えないことです。 コンピュータービジョンは、開始以来非常に長い間、関連する問題に直面しており、定期的に効果的な特定のソリューションを見つけました-したがって、画像全体でテストパターンを連続的に移動するオブジェクトを識別できます(畳み込みネットワークが正常に使用します)。 SIFT、SURF、およびORB属性を使用してスケーリングまたは回転した画像ですが、シーン空間内のオブジェクトの遠近感と回転の効果は、質的に異なるレベルにあるようです。 ここでは、真の3次元形状を得るために、オブジェクトがすべての側面からどのように見えるかを知る必要があります。そうでない場合は、何も処理しません。 したがって、写真を認識するために、写真を認識する必要はありません。 彼らは虚偽で、欺ce的で、故意に劣っています。 彼らは私たちの友達ではありません。
3.最後に、練習する(実際にはしない)
だから、重要な問題は、私たちが見るすべての3次元モデルをどのように取得するのでしょうか? さらに重要な質問は、レーザー空間スキャナーを購入せずにうまくやっていく方法です(最初に「非常に高価なレーザースキャナー」を書いてから、 この記事に出くわしました )。 申し訳ありませんが、視覚システムの進化の過程にある動物は、明らかにそれなしで、目だけで何とかして管理されているので、それほど多くはありません。
この場所のどこかで、観客の一部が立ち上がって部屋を出て、機器に刻印することを呪います-誰もが私たちが深さと空間を知覚するために両眼視を使用していることを知っています、これには2つの特別な目があります! あなたもそう思うなら、あなたには少し驚きがあります-これは真実ではありません。 証明はシンプルで美しい-片目を閉じて部屋を歩き回って、世界が突然深さを失い、アニメの平らなアナログのように見えないことを確認してください。 もう1つの方法は、モニターの完全に平らな表面に位置しているにもかかわらず、奥に戻って鉄道の写真をもう一度見ることです。
一般に、2つの目ではそれほど単純ではありません
一部のアクションでは、空間的位置を評価するという点で非常に有益なようです。 2本の鉛筆を取り、片目を閉じ、これらの鉛筆を動かして、顔の近くのリードの先端に触れるようにします。 ほとんどの場合、リードは分離し、顕著になります(成功した場合は、顔にさらに近づけます)が、これは2番目の開いた目では発生しません。 マークチャンギシの著書「Revolution in Vision」の例です。立体視と双眼視についての章全体があり、垂れ葉のような小さなノイズを見るために2つの目を見る必要があるという奇妙な理論があります。 ところで、面白い事実-ウィキペディアの両眼視の利点のリストの最初の場所にあるのは、「1つが損傷した場合にクリーチャーに予備の目を与える」ということです。
そのため、両眼視は私たちには適していません。ステレオカメラ、レンジファインダー、Kinectは拒否されます。 私たちの視覚システムが私たちが見ているものの3次元画像を再現する能力が何であれ、それは明らかに2つの目を必要としません。 結果は何ですか?
私は、生物学的視覚に関して正確な答えを出す準備ができているわけではありませんが、おそらく、カメラ付きの抽象的なロボットの場合、目ではなく有望な方法が残っています。 そして、これが動きです。
電車のトピックに戻りますが、今回は窓の外を見るだけです。

この場合に見られるものは「運動の視差」と呼ばれ、簡単に言えば、横に移動すると、近くの物体が遠くの物体よりも視野内で移動するという事実にあります。 前後に移動してターンするために、適切なルールを策定することもできますが、ここではそれらを無視しましょう。 そのため、移動してフレーム内のオブジェクトの変位を評価し、これに基づいてオブザーバーからの距離を決定します。これは正式には「動きからの構造」と呼ばれる手法です。 やってみましょう。
4.最後に、練習する
まず第一に-しかし、彼らは私たちの前に、偶然、すべてをしましたか? ウィキペディアの「モーションからの構造」ページには、ビデオまたは写真のセットから3Dモデルを再作成するための13のツール(および唯一のオープンソース)があり、そのほとんどがバンドル調整と呼ばれるアプローチを使用しており、彼はクールです)。 残念ながら、これはまだ遭遇する問題を引き起こします-Bundlerはカメラモデルとその内部パラメーターを私たちから知りたいと思っています(極端な場合、モデルが不明な場合、焦点距離を指定する必要があります)。
これがあなたのタスクにとって問題ではない場合、それは最も簡単で同時に効果的な方法であるため、読書を安全に終了することができます(ところで、ゲームEthan Carter Disappearanceのモデルがほぼ同じ方法で作られたことを知っていますか?) 残念ながら、カメラモデルに縛られる必要があるということは、避けたい条件です。 まず、私たちの側には完全なYouTubeビジュアルビデオエクスペリエンスがあり、将来サンプルとして使用したいからです。 第二に(そして、これはおそらくさらに重要です)、人間の脳は、目のカメラの内部パラメーターを数字で知っていれば、光学歪みに適応する方法を完全に知っているようだからです。 広角カメラ、魚眼レンズのレンズを通して見る、映画を見る、そしてオクルスライフルを装着しても、視覚能力が完全に損なわれることはありません。 したがって、おそらく、他の方法が可能です。
そこで、残念
1.キャリブレーションされたカメラから2つのフレームを撮影します。
2.キャリブレーションパラメーター(カメラマトリックス)とともに、両方をstereoRectify関数に配置します。これにより、これら2つのフレームが直線化(修正)されます。これは、ポイントとそのオフセットが1本の水平線に現れるように画像を歪める変換です。
3.これらの修正されたフレームをstereoBM関数に入れて、視差マップを取得します-グレーの濃淡で、ピクセルが明るく、オフセットが大きくなるような画像(参照例があります)。
4.結果のディスプレイスメントマップを、 reprojectImageTo3Dという名前の関数に入れます(Qマトリックスも必要です。これは、特にステップ2で取得します)。 3次元の結果が得られます。
くそー、私たちは同じレーキを踏んでいるようです-すでにポイント1では、キャリブレーションされたカメラが必要です(ただし、OpenCVは私たち自身でそれを行う機会を与えてくれます)。 しかし、ちょっと、計画Bがあります。不審な名前stereoRectifyUncalibratedを持つドキュメントの機能があります...
プランB:
1.少なくとも限られたポイントのセットについて、変位のおおよその部分を自分で評価する必要があります。 StereoBMはここでは適切ではないため、他の方法が必要です。 論理的なオプションは、フィーチャマッチングを使用することです。両方のフレームでいくつかの特別なポイントを見つけて、マッピングを選択します。 この方法については、 こちらをご覧ください 。
2.互いに対応する2セットのポイントがある場合、それらをfindFundamentalMatにドロップして、 stereoRectifyUncalibratedに必要な基本マトリックスを取得できます。
3. stereoRectifyUncalibratedを実行し、両方のフレームを修正するための2つのマトリックスを取得します。
4.そして...そしてそれは明確ではありません。 フレームを修正しましたが、最終ステップに必要な行列Qはありません。 グーグルで、私は同じ困惑についての投稿につまずき、理論的に何かを見逃したか、この瞬間がOpenCVで考えられなかったことに気付きました。
OpenCV:2-0です。
4.1計画の変更
しかし、ちょっと。 おそらく最初から間違った方向に進んだのでしょう。 以前の試みでは、実際に、3次元ポイントの実際の位置を決定しようとしました。したがって、カメラ、マトリックス、フレームの修正などのパラメーターを知る必要がありました。 実際、これは通常の三角測量です:最初のカメラでこの点を見て、2番目でここで-私たちはカメラの中心を通る2つの光線を描き、それらの交点は点が私たちからどれだけ離れているかを示します。
これで十分ですが、一般的に言えば、必要ありません。 後で何らかの目的で3Dプリンターでモデルを使用した場合、オブジェクトの実際のサイズに興味があります。 しかし、受信したデータをニューラルネットワークおよび同様の分類器にプッシュするために(ただし、この目標は既に少しぼやけています)。 このためには、オブジェクトの相対的なサイズのみを知るだけで十分です。 私たちがまだ覚えているように、それらは視差変位に反比例します-私たちから遠く離れるほど、それは私たちの移動中に移動しません。 どうにかして2つの写真を比較するだけで、これらの変位をさらに簡単に見つけることは可能ですか?
もちろんできます。 こんにちは、 光ストリーム 。
これは、まさに必要なことを行う素晴らしいアルゴリズムです。 その中に写真とポイントのセットを入れます。 次に、2番目の画像を配置します。 与えられたポイントの出力で、2番目の画像の新しい位置を取得します(もちろん概算です)。 キャリブレーションやカメラの言及は一切ありません-オプティカルフローは、名前にかかわらず、何に基づいても計算できます。 通常、オブジェクトの追跡、衝突の検出、さらには拡張現実にまで使用されます。
私たちの目的のために、(今のところ)Gunnar Farnebakの「密な」フローを使用したいと思います。彼は、個々のポイントではなく、全体像を一度に計算する方法を知っているからです。 このメソッドはcalcOpticalFlowFarnebackで使用できます。最初の結果は本当に本当に始まります。以前の結果stereoRectifyUncalibrated + stereoBMよりもどれだけクールに見えるかを確認してください。

素晴らしいゲームPortal 2に、あなた自身の部屋を作り、キューブをプレイする機会に感謝します。 私は科学をやっています!
この小さなデモのコード
# encoding: utf-8 import cv2 import numpy as np from matplotlib import pyplot as plt img1 = cv2.imread('0.jpg', 0) img2 = cv2.imread('1.jpg', 0) def stereo_depth_map(img1, img2): # 1: feature matching orb = cv2.ORB() kp1, des1 = orb.detectAndCompute(img1, None) kp2, des2 = orb.detectAndCompute(img2, None) bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True) matches = bf.match(des1, des2) matches = sorted(matches, key=lambda x: x.distance) src_points = np.vstack([np.array(kp1[m.queryIdx].pt) for m in matches]) dst_points = np.vstack([np.array(kp2[m.trainIdx].pt) for m in matches]) # 2: findFundamentalMat F, mask = cv2.findFundamentalMat(src_points, dst_points) # 3: stereoRectifyUncalibrated _, H1, H2 = cv2.stereoRectifyUncalibrated(src_points.reshape(src_points.shape[ 0], 1, 2), dst_points.reshape(dst_points.shape[0], 1, 2), F, img1.shape) rect1 = cv2.warpPerspective(img1, H1, (852, 480)) rect2 = cv2.warpPerspective(img2, H2, (852, 480)) # 3.5: stereoBM stereo = cv2.StereoBM(cv2.STEREO_BM_BASIC_PRESET, ndisparities=16, SADWindowSize=15) return stereo.compute(rect1, rect2) def optical_flow_depth_map(img1, img2): flow = cv2.calcOpticalFlowFarneback(img1, img2, 0.5, 3, 20, 10, 5, 1.2, 0) mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1]) return mag def plot(title, img, i): plt.subplot(2, 2, i) plt.title(title) plt.imshow(img, 'gray') plt.gca().get_xaxis().set_visible(False) plt.gca().get_yaxis().set_visible(False) plot(u' ', img1, 1) plot(u' ( )', img2, 2) plot(u'stereoRectifyUncalibrated', stereo_depth_map(img1, img2), 3) plot(u' ', optical_flow_depth_map(img1, img2), 4) plt.show()
すごい ディスプレイスメントがありますが、かなり良く見えます。 どのようにしてそれらから3次元ポイントの座標を取得できますか?
4.2 3次元の点の座標を取得する部分
この図は、上記のリンクのいずれかで既にちらついています。
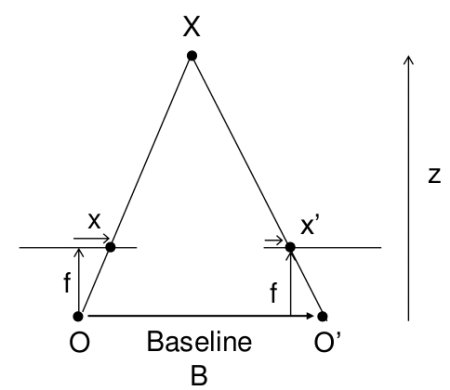
ここでのオブジェクトまでの距離は、学校のジオメトリメソッド(類似の三角形)を使用して計算され、次のようになります。
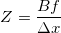 。 そして、それぞれ次のような座標:
。 そして、それぞれ次のような座標: 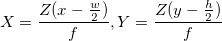 。 ここで、 wとhは画像の幅と高さで、 fはカメラの焦点距離(カメラの中心から画面の表面までの距離)、 Bはカメラのステップです。 ちなみに、ここでZを上に向けると、Zが画面に「深く」見え、XとYがそれぞれ画像の幅と高さに沿って向けられているため、一般的に受け入れられている軸の名前に若干違反していることに注意してください。
。 ここで、 wとhは画像の幅と高さで、 fはカメラの焦点距離(カメラの中心から画面の表面までの距離)、 Bはカメラのステップです。 ちなみに、ここでZを上に向けると、Zが画面に「深く」見え、XとYがそれぞれ画像の幅と高さに沿って向けられているため、一般的に受け入れられている軸の名前に若干違反していることに注意してください。
さて、 fに関しては、すべてが単純です。すべてのオブジェクトの割合だけが1つの法則に従って変化した場合、カメラの実際のパラメーターは興味がないことを既に規定しています。 上記のXの式でZを代入すると、Xは焦点距離に依存しないことがわかります(fが減少します)。したがって、その異なる値は深度を変更するだけです-シーンを「ストレッチ」または「フラット」にします。 視覚的には、あまり良くありませんが、分類アルゴリズムについては、まったく同じです。 それでは、知的な方法で焦点距離を設定しましょう-考えてみてください。 確かに、私は本文でさらに少し心を変える権利を留保します。
Bについては、もう少し複雑です。歩数計が組み込まれていない場合、現実世界でカメラがどれだけ動いたかわかりません。 そのため、ここでは少し数えて、カメラがほぼスムーズに移動し、多くのフレーム(1秒間に数十個)があり、2つの隣接するフレーム間の距離がほぼ同じであると判断します。
 。 繰り返しになりますが、さらにこの状況を少し明確にしますが、今のところはそうさせてください。
。 繰り返しになりますが、さらにこの状況を少し明確にしますが、今のところはそうさせてください。
いくつかのコードを書く時間です
import cv2 import numpy as np f = 300 # , - , B = 1 w = 852 h = 480 img1 = cv2.imread('0.jpg', 0) img2 = cv2.imread('1.jpg', 0) flow = cv2.calcOpticalFlowFarneback(img1, img2, 0.5, 3, 20, 10, 5, 1.2, 0) mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1]) edges = cv2.Canny(img1, 100, 200) result = [] for y in xrange(img1.shape[0]): for x in xrange(img1.shape[1]): if edges[y, x] == 0: continue delta = mag[y, x] if delta == 0: continue Z = (B * f) / delta X = (Z * (x - w / 2.)) / f Y = (Z * (y - h / 2.)) / f point = np.array([X, Y, Z]) result.append(point) result = np.vstack(result) def dump2ply(points): # .ply, with open('points.ply', 'w') as f: f.write('ply\n') f.write('format ascii 1.0\n') f.write('element vertex {}\n'.format(len(points))) f.write('property float x\n') f.write('property float y\n') f.write('property float z\n') f.write('end_header\n') for point in points: f.write('{:.2f} {:.2f} {:.2f}\n'.format(point[0], point[2], point[1])) dump2ply(result)
これは結果がどのように見えるかです。 あなたがこの場所を読んでいる間、このgifがロードできたことを願っています。
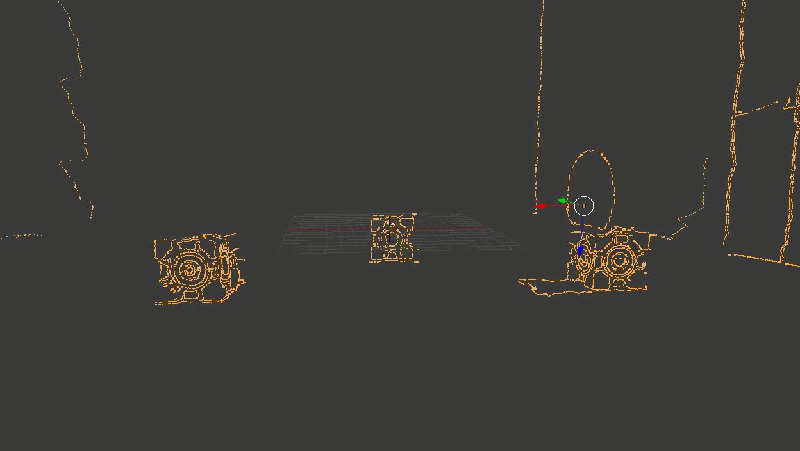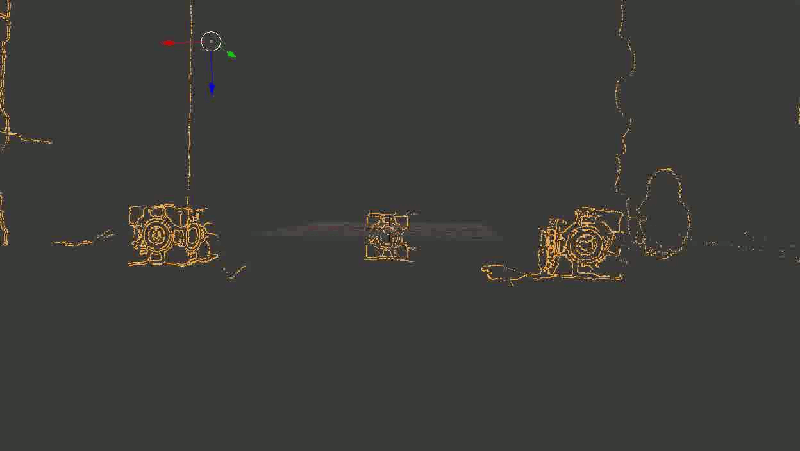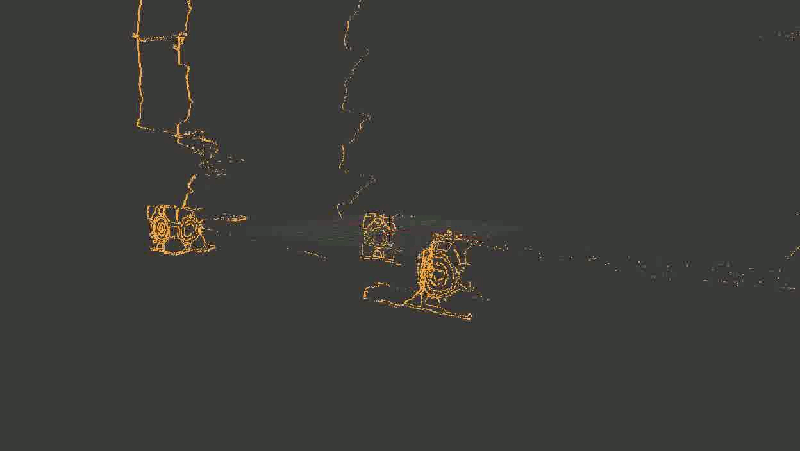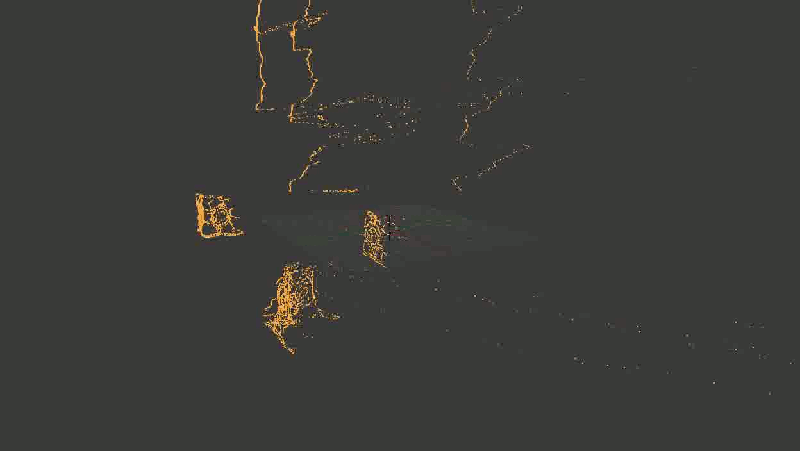
わかりやすくするために、すべてのポイントを連続して取得したのではなく、Canny検出器によって強調表示された境界のみを取得しました
一見したところ(とにかく、私にとって)すべてが優れているように見えた-立方体の面の間の角度でさえかなり90度を形成した。 背景にオブジェクトがあると悪化しました(壁とドアの輪郭がどのように歪んでいるかに注意してください)が、ちょっとしたノイズである可能性があります。フレームを増やすか、他の何かを使用して修復できます。
ここに描かれる可能性のあるすべての性急な結論のうち、これは真実から最も遠いことが判明しました。
5.何も起こらない部分
一般的に、主な問題は、いくつかのポイントがかなり歪んでいることが判明しました。 そして-何かが間違っていると疑う時間である警告サインは、ランダムではなくほぼ同じ場所で歪められたため、(他のフレームから)新しいポイントを連続して適用することで問題を修正することはできませんでした。
次のようになりました。 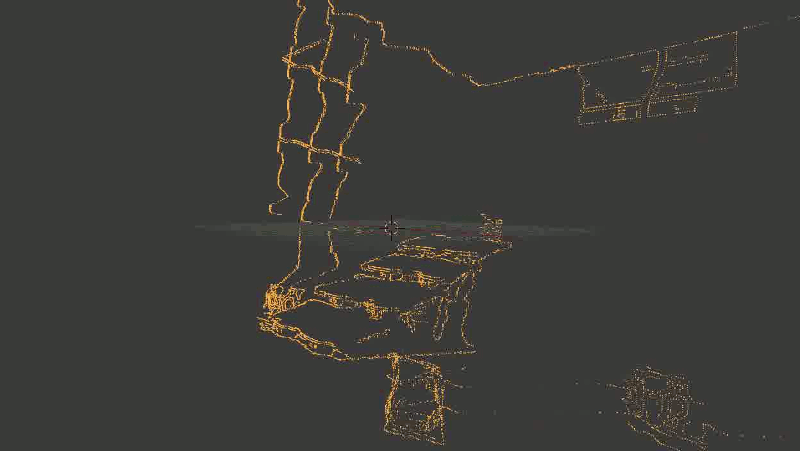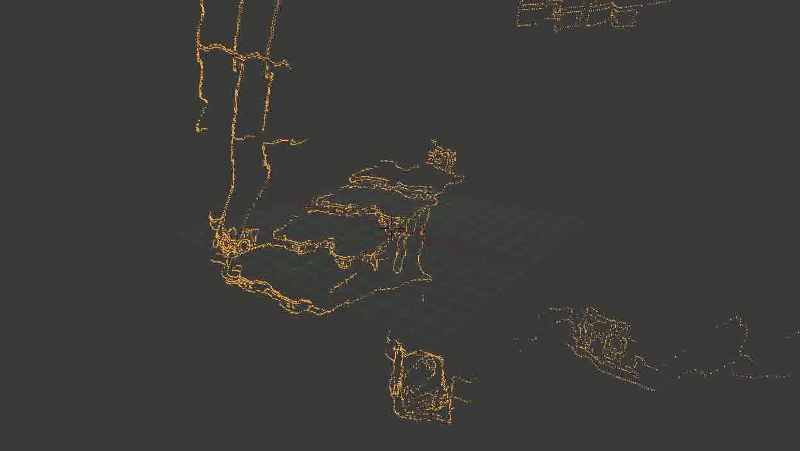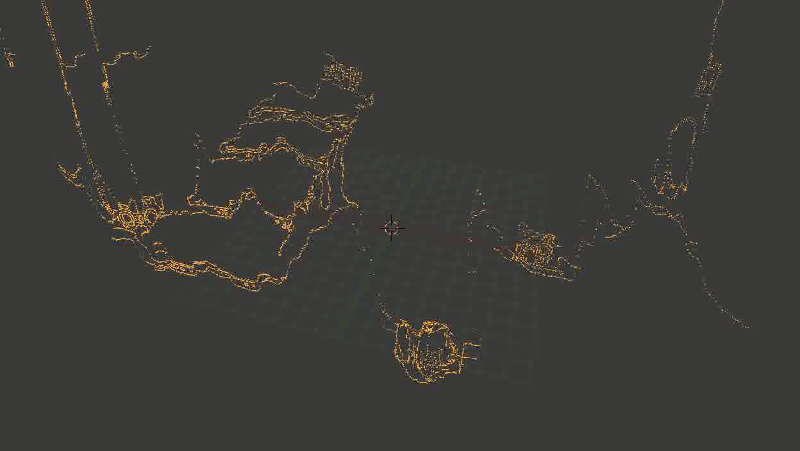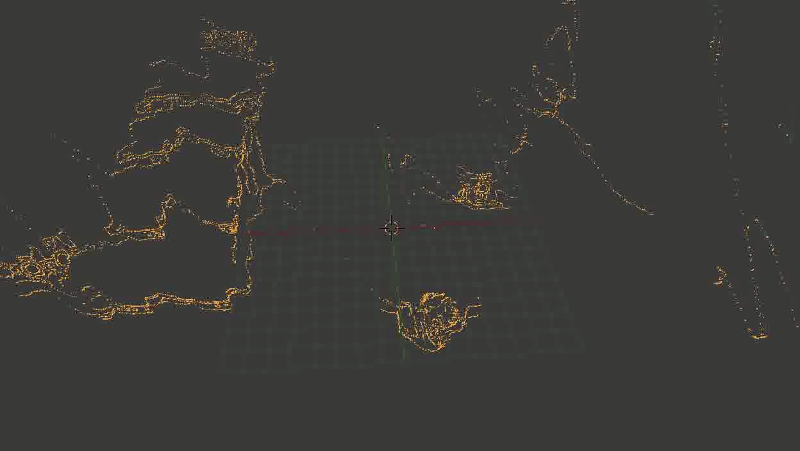
階段は崩壊し、時には不可解なものの不定形な部分に変わります。
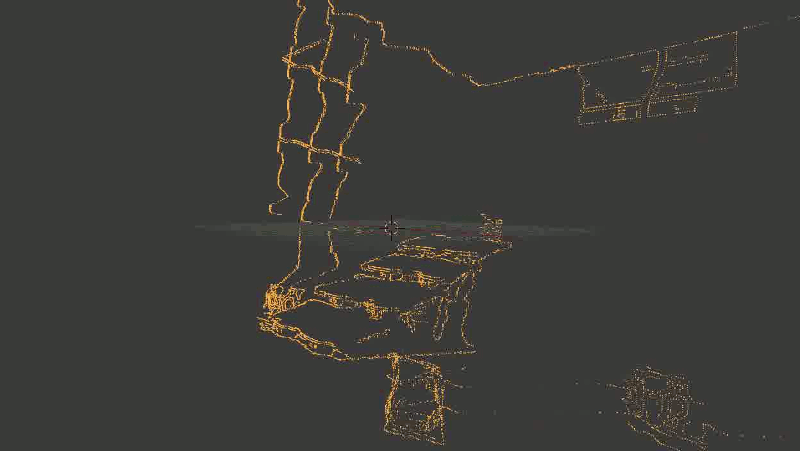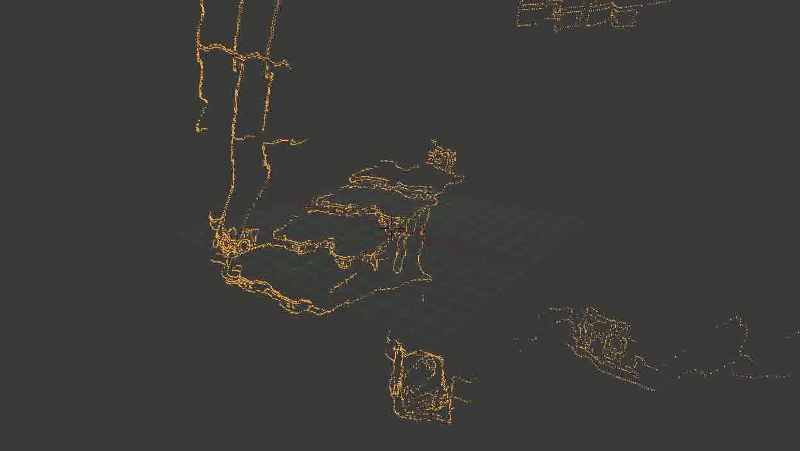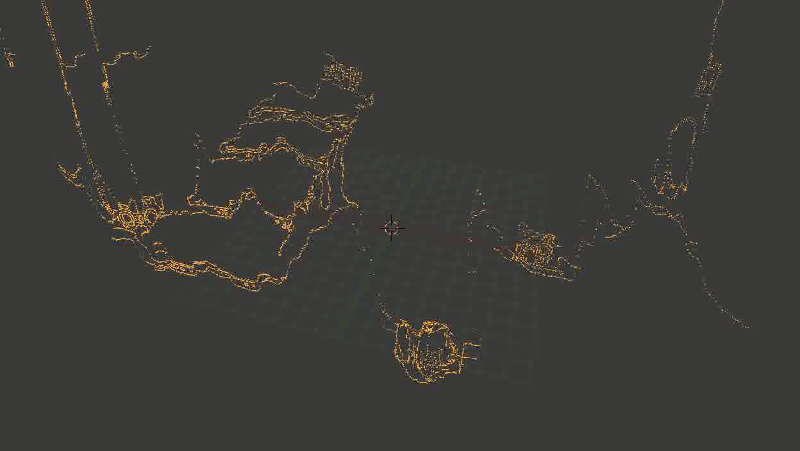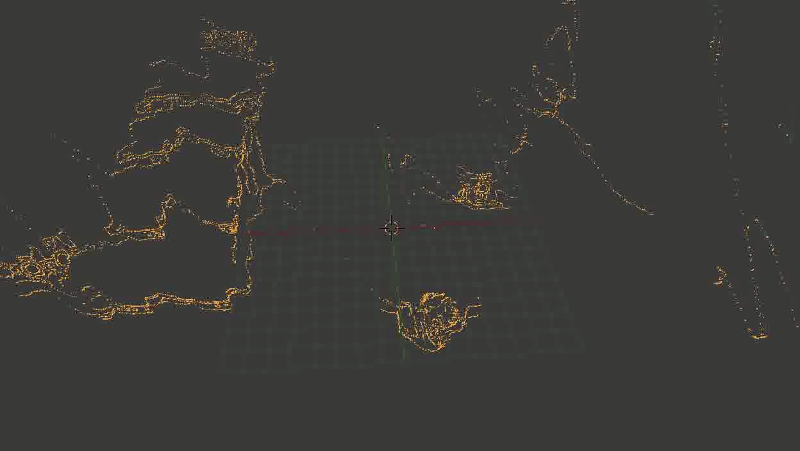
階段は崩壊し、時には不可解なものの不定形な部分に変わります。
私は非常に長い間それを修正しようとしましたが、この間に私は次のことを試しました:
-光学ストリームでカリンカを滑らかにします:ガウスぼかし、メディアンフィルター、シャープなエッジを残すファッショナブルなバイラテラルフィルター。 それは役に立たない:反対に、オブジェクトはさらにぼやけます。
-ハフ変換を使用して画像内の直線を見つけて、変更されていない直線状態で転送しようとしました。 部分的には機能しましたが、境界でのみ-表面はまだ歪んだままです。 さらに、「画像に直線がまったくない場合はどうする」という精神では、どこにもうまくいきませんでした。
-OpenCVのtemplateMatchingを使用して、独自のバージョンの光ストリームを作成しようとしました。 これは次のように機能しました。どのポイントでも、小さな(約10x10)正方形を周囲に構築し、動き回って最大一致を探します(動きの方向がわかっている場合は、「周囲」を制限できます)。 場所によってはかなりうまくいきました(ただし、元のバージョンより明らかに動作が遅くなりました)。

左側にはおなじみのファーンバックストリーム、右側には上記の自転車があります
残念ながら、ノイズに関しては、それは良くないことが判明しました。
一般に、すべてが悪いものでしたが、非常に論理的です。 あるべき姿だったから。
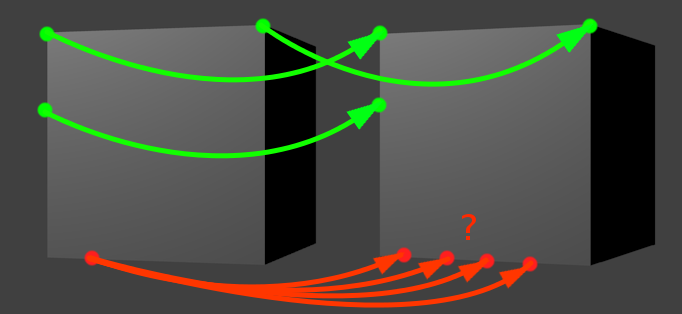
問題の図。 ここの動きはまだ右への一歩です
上の写真から緑色の点を選んでみましょう。 移動の方向がわかっていて、指定された方向に移動している緑の点の「シフトした双子」を探すとします。 探している双子を見つけたと判断するのはいつですか? ある種の「ランドマーク」に出くわすと、出発点の環境に似た特徴的な領域になります。 たとえば、斜めに。 この点での角度は、それら自体が非常にまれであるため、追跡が容易です。 したがって、緑の点が角度であり、特定の近傍で同様の角度が見つかった場合、問題は解決されます。
もう少し複雑ですが、縦線の状況はまだ簡単です(2番目の左の緑の点)。 私たちが右に移動していることを考えると、垂直線は検索期間全体で一度だけ会います。 画像を介して検索ボックスをクロールし、無地の背景、背景、背景をもう一度、垂直セグメント、背景をもう一度、背景、および背景をもう一度見ると想像してください。 それも簡単です
問題は、動きと平行な線を追跡しようとするときに現れます。 赤い点には、追放された双子の役割の明確な候補はありません。 それらの多くがあり、それらはすべて近くにあり、私たちが使用する方法を使用してそれらのいずれかを選択することは単に不可能です。 これはオプティカルフローの機能制限です。 対応する記事でウィキペディアから親切に警告されているように、「この1つの方程式を2つの未知の変数で解くことはできません」とあなたにできることは何もありません。
何もありませんか?
一般に、正直に言うと、これはおそらくあまり真実ではありません。 結局のところ、右の写真に赤い点を見つけることができますか? これもそれほど難しいことではありませんが、このために他の方法を精神的に使用します-近くの最も近い「緑の点」(下隅)を見つけ、それまでの距離を推定し、対応する距離を立方体の2番目の面に置きます。 オプティカルフローアルゴリズムには成長の余地があります-この方法を採用することもできます(まだ行っていない場合)。
6.緑色のドットFTW
実際、遅れた常識がこの時点で私たちに告げているように、私たちは最終的な目標-認識、分類、および他の知性にとって重要ではない余分な作業をまだ試みています。 写真のすべてのポイントを3次元の世界に詰め込もうとするのはなぜですか? 2次元画像を使用する場合でも、通常、各ピクセルを分類に使用しようとはしません。ほとんどのピクセルには有用な情報が含まれていません。 ここで同じことをしないのはなぜですか?
実際、すべてがとてもシンプルでした。 同じ光束を計算しますが、「緑色」の安定点のみです。 ちなみに、OpenCVではすでに彼らが私たちの面倒を見てくれました。 必要なものはLucas-Canadaストリームと呼ばれます。
同じ場合のコードと例を提供するのは少し退屈です。なぜなら、同じことになるが、ポイント数がはるかに少ないからです。 途中で何か他のことをしましょう。たとえば、カメラの回転を処理する機能をアルゴリズムに追加します。 その前に、私たちは専ら横に移動しましたが、現実の世界では列車の窓の外は非常にまれです。
ターンの出現により、X座標とZ座標が混ざります。 カメラに相対的な座標を計算するための古い式はそのままにして、次のように絶対座標に変換します(ここで
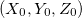 -カメラ位置の座標、アルファ-回転角度):
-カメラ位置の座標、アルファ-回転角度):
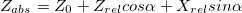
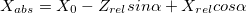

(プレーヤーは詐欺師です;これは、カメラが上下に動かないと信じているためです)
ここのどこかで焦点距離に問題があります-覚えておいて、私たちはそれをask意的に決めたのですか? そのため、異なる角度から同じポイントを評価する機会が得られたので、X座標とZ座標が互いに干渉し始めたため、それが重要になりました。 実際、前のコードに似たコードを任意のフォーカスで実行すると、次のようなコードが表示されます。

明らかではありませんが、これは通常の立方体の周りにカメラツアーを配置する試みです。 各フレームは、カメラの次の回転後の可視ポイントの推定値です。 ミニマップのような平面図。
幸いなことに、まだ光ストリームがあります。 回転するとき、どのポイントがどのポイントに変わるかを確認し、2つのビューの角度からそれらの座標を計算できます。 ここから焦点距離を取得するのは簡単です(異なるアルファ値に対して上記の2つの式を取得し、座標を同等にし、fを表現するだけです)。 はるかに良い:
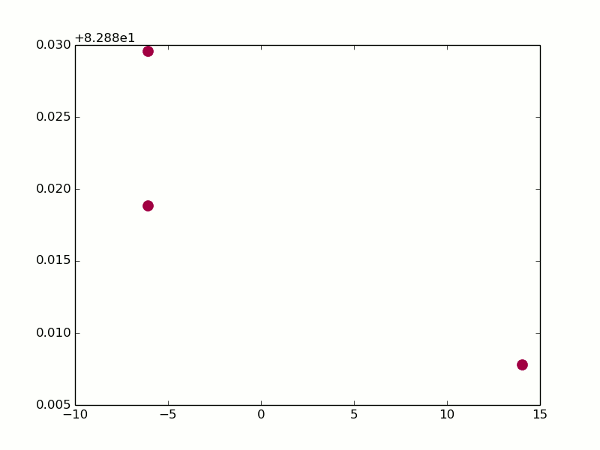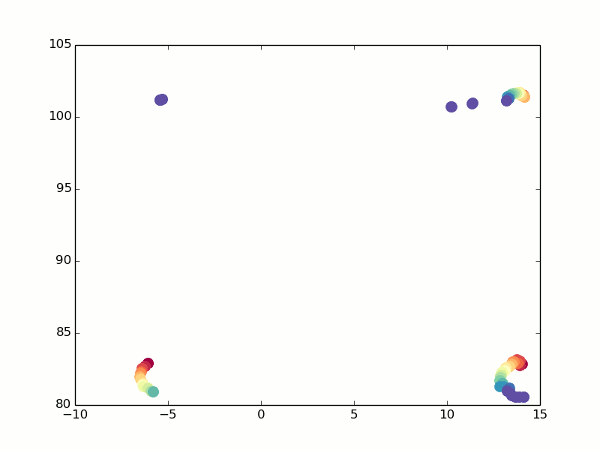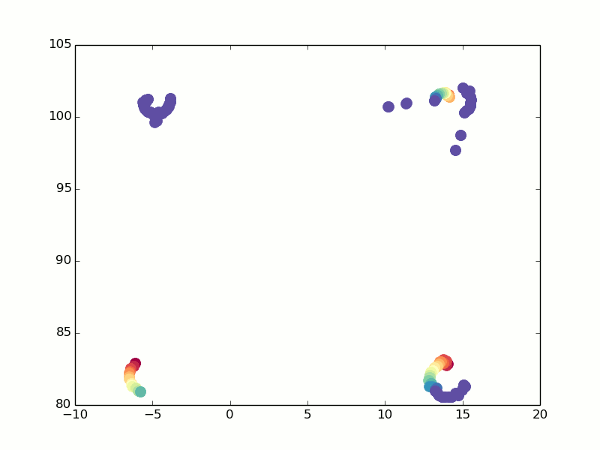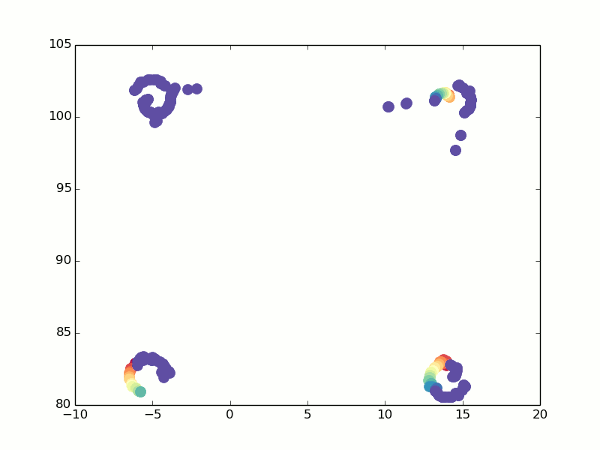
すべてのポイントが互いに完全に適合するわけではありませんが、少なくとも立方体であると推測できます。
最後に、ポイントの位置の推定値が必ずしも一致しないため、何らかの方法でノイズに対処する必要があります(きちんとした不均一なリングの上のgifを参照してください。それぞれの代わりに、理想的には1つのポイントがあるはずです)。 すでに創造性の余地はありますが、私には次のような最も適切な方法がありました。
-横に複数のシフトがある場合、それらの情報を結合します。したがって、1つのポイントについて、一度に複数の深度推定値が得られます。
-カメラが回転すると、2セットのポイントを組み合わせて(ターンの前後)、一方を他方に合わせようとします。 このフィッティングは適切に「ポイント登録」と呼ばれます(文脈から外れた用語を聞いた場合は想像もしなかったでしょう)。そのために、Python + OpenCVのgoogleバージョンの反復最近傍点アルゴリズムを使用しました。
-次に、しきい値半径(最近傍法で決定)内にあるポイントがマージされます。 各ポイントについて、「強度」のようなものを追跡します。これは、他のポイントと組み合わされた頻度のカウンターです。 強度が大きいほど、それが正直で正しいポイントである可能性が高くなります。
結果は、ポータルのキューブの場合ほど安定していませんが、少なくとも正確です。 以下は、私が最初にBlenderにアップロードし、カメラをひねってフレームを保存した、再作成されたモデルです。
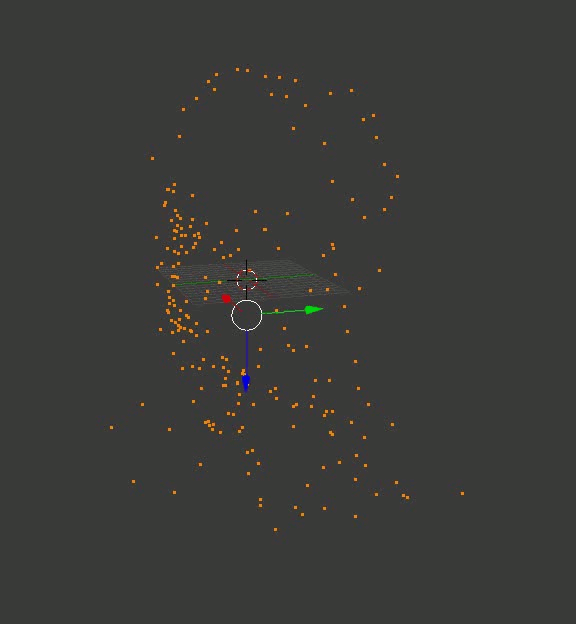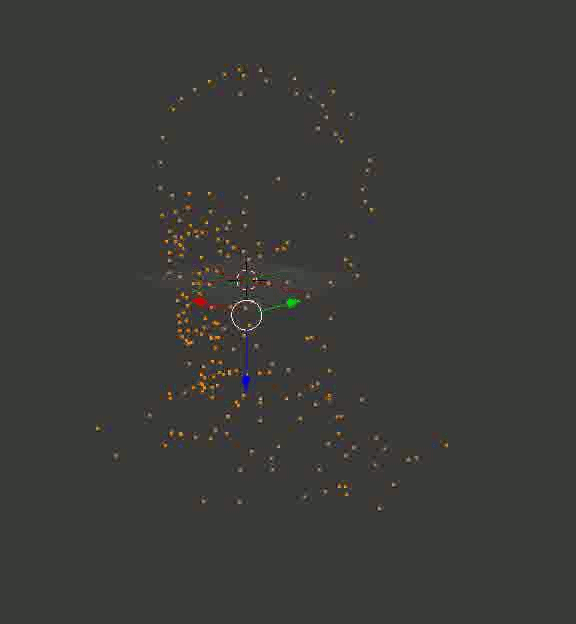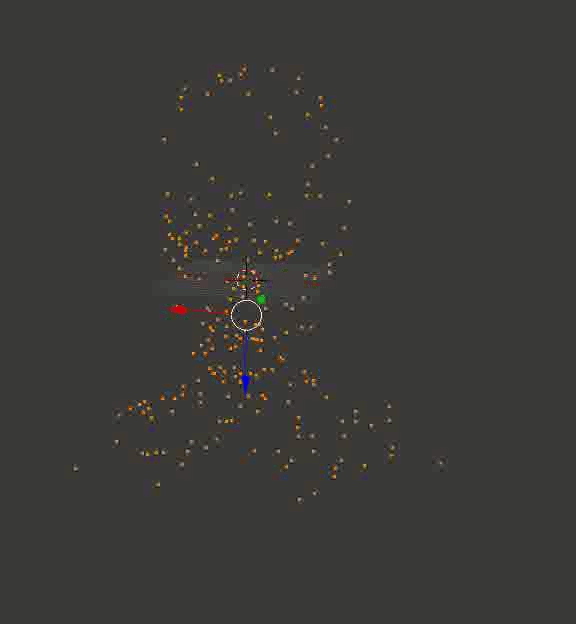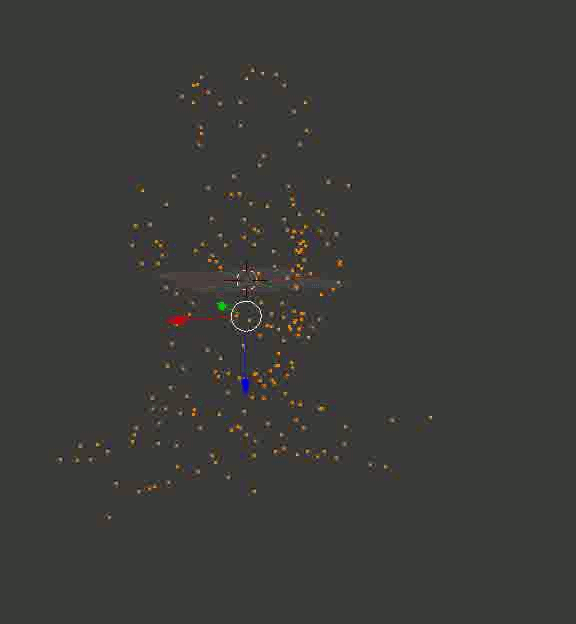
ダウエル教授の頭

ある種のランダムな車
ビンゴ! 次に、それらすべてを認識アルゴリズムに詰め込み、何が起こるかを確認する必要があります。 しかし、これはおそらく、次のシリーズに向けて出発します。
アプリ
少し振り返って、なぜこれをすべて行ったのかを思い出しましょう。 推論の行は次のとおりでした。
-写真に描かれているものを認識できる必要があります
-しかし、これらの写真は、位置を変えたり、同じものを異なる角度から見たりするたびに変わります。 時々認識を超えて
-これはバグではなく機能です:私たちの限定されたアイセンサーは、被写体全体ではなく被写体の一部のみを見るという事実の結果
-したがって、何らかの方法でセンサーからのこれらの部分データを組み合わせて、完全な形で被験者のアイデアを収集する必要があります。
一般的に言えば、これは確かに視覚の問題だけではありません 。 これはルールであり、例外ではありません-私たちのセンサーは全能ではなく、部品のオブジェクトに関する情報を常に認識しています-しかし、そのようなすべてのケースをある種の一般的なフレームワークにどれだけ組み合わせることができるのでしょうか? 言います(視界に戻る)、あなたの目は常に小さくて非常に速い動きをしています-サッカード-視野内のオブジェクト間をジャンプします(そして、これらの動きの間隔であなたのビジョンはまったく機能しません-鏡を見ても自分のサッカードを見ることができない理由です空白)。 脳は、見られる部分を「縫い合わせる」ために常に努力を続けています。 これは私たちが解決しようとしたばかりの問題ですか、それともまだ違いますか? 単語の発音のさまざまなバリエーションを「理想的な」スペルの1つと相関させることができる場合の音声認識。これも同様のタスクですか。 シノニムをアイテムの1つの「イメージ」に減らすとどうなりますか?
はいの場合、それは可能です、問題は視覚システムの単なる小さな町のアルゴリズムではなく、スキャナーのレーザーポインターを進化していない目で置き換えるだけではありません。
自然界に見られるものを再現しようとするとき、そのすべてのコンポーネントを盲目的にコピーすることは意味がないということは明らかな考慮事項です。 空を飛ぶために、羽ばたきの羽と羽、十分に硬い羽と揚力は必要ありません。 速く走るために、機械的な脚は必要ありません-車輪ははるかによく対処します。 私たちが見たものをコピーするのではなく、原則を見つけて自分でそれを繰り返したいと思います(たぶんそれをより簡単/より効率的にする)。 飛行の空力の法則の類似物である知性の原理は何ですか、まだわかりません。 ディープラーニングと彼の預言者であるYan Lekun(および彼の後の多くの人々)は、受け取ったデータから機能の「深い」階層を構築する能力に目を向ける必要があると考えています。 これにもう1つ説明を加えることができます。関連するデータを1つのオブジェクトの一部として認識し、新しい次元に配置する機能です。