まえがき
暇なときに、面白いことをすることにしました。 キャンバスの小さなフレームワークを書くというアイデアが思い浮かびました(自転車ですが、それも面白いです)。 ベジエ曲線になりました。
組み込みのソリューションを何らかの形で装飾することにしましたが、欠点が1つあります。 問題は、二次曲線と三次曲線の関数が、編集できない既製の結果を与えることです。 曲線を徐々に輪郭を描くか、曲線の一部のみを輪郭を描く必要がありました。2〜3度を超える次数の曲線の輪郭を描きたいという事実は言うまでもありません。
私はグーグルを始めました。 Habréに関する興味深い記事を見つけました。 しかし、数学に関する私の知識は、それを自分のニーズに変換することを許可しませんでした。さらに、タイマーがそこで使用されているため、時間通りにアニメーションを停止することはできません。
私はゼロから書き始めています。
すべてがそれほど怖くないことが判明しました。 de Costeljoアルゴリズムの本質自体は単純であるため、なぜこのような独創的な式を使用するのでしょうか? だから私はしません。
アルゴリズムについて簡単に説明してから、サンプルコードについて説明します。
曲線を計算する関数は、オフセット(つまり、曲線の始点からの距離(パーセント))だけをポイントとして返します。 オフセットを徐々に増やすと、ポイントが増えます。 必要に応じて、アルゴリズムを停止できます、美しさ! また、タイマーの束は必要ありません。1つのsetIntevalだけで、ポイントを段階的に照会して概要を示します。
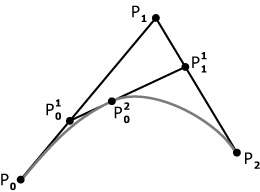
getPointOnCurve関数は、渡されたポイントからセグメントを再帰的に計算します。
計算後、変位により、これらのセグメント上の新しいポイントを見つけ、それを自身に渡します。 戻る曲線上でポイントが見つかるまで継続します。
// formula formula.getPointOnCurve = function(shift,points){ if(points.length == 2){ return this.getPointOnLine(shift,points); } var pointsPP = []; for(var i = 1;i < points.length;i++){ // getPointOnLine , . pointsPP.push(this.getPointOnLine(shift,[ points[i - 1], points[i] ])); } return this.getPointOnCurve(shift,pointsPP); };
ヘルパー関数getPointOnLine:
formula.getPointOnLine = function(shift,points){ //, points : [[x0,y0],[x1,y1]] return [ (points[1][0] - points[0][0]) * (shift / 100) + points[0][0], (points[1][1] - points[0][1]) * (shift / 100) + points[0][1] ]; };
そして、図面自体は次のとおりです。
// var points = [ [10,50], [40,-40], [190,180], [40,-60], [80,130], [10,50] ];// var shift = 0; var step = 1;// shift step var timer = setInterval(function(){ context.beginPath(); context.moveTo(points[0][0],points[0][1]); if(shift > 101){ shift = 101; } for(var i = 0;i <= shift;i += step){ var coord = formula.getPointOnCurve(i,points); context.lineTo(coord[0],coord[1]); } context.closePath(); if(shift <= 100){ shift += step; } },fps)
そして、もちろん、 例 。
私自身が長い間理解できなかったので、誰かが助けてくれたことを願っています。