Oleksandr Pavlykによる投稿の翻訳、「 Jacob Bernoulli's Legacy in Mathematica 」。
Mathematicaドキュメントの形式で翻訳をダウンロードできます。このドキュメントには、記事で使用されているすべてのコードと追加資料が含まれています 。
2015年1月16日は、 ジェイコブベルヌーイ生誕360周年です。
[1]で：=
アウト[2] =
[3]で：=
アウト[3] =
[4]で：=
アウト[4] =
ヤコブ・ベルヌーイは、有名なベルヌーイ家の最初の数学者となり、XVII世紀およびXVIII世紀の多くの有名な数学者が属します。
ヤコブベルヌーイの数学的遺産は非常に豊富です。 彼はいわゆるベルヌーイ数を導入し（ Wiki / MathWorld ）、 ベルヌーイ微分方程式 （ Wiki / MathWorld ）の解を見つけ、ベルヌーイ過程 （ Wiki / MathWorld ）を研究し、ベルヌーイ不等式 （ Wiki / MathWorld ）を証明し 、 数e （ Wiki / MathWorld ）を計算し、また、多数の弱い法則 （ベルヌーイの定理）（ Wiki / MathWorld ）を明らかにしました。
[5]で：=
アウト[5] =
ベルヌーイの論文Ars Conjectandi （ The Art of Conjecturing - The Art of Assumption）は、彼の死から8年後の1713年に死後に出版され、当時の共通語であるラテン語で書かれていました。 それは確率論の基本的な仕事と見なされます。 その重要性は、特に、1801年にG. Le Roy によってフランス語に翻訳され、最近では2005年にED Sylla によって英語に翻訳されたという事実によって証明されています。
Ars Conjectandiは4つの部分で構成されています。 最初の部分は、Ludo Aleaeの Christian Huygens De Ratiociniisの作品を再現しています。 （ チャンスのゲームの推論について -ギャンブルの計算について）ベルヌーイによる広範なコメントと、ホイヘンスの仕事の終わりに提示された5つのホイヘンスの問題に対する詳細な解決策と答えがありますが、証拠はありません。 最初の部分では、ベルヌーイは、各試行の成功確率がpである場合、 n回の独立した試行の中で少なくともm回成功する確率も推定します。
「順列と組み合わせの教義」の第2部は、組み合わせ論とカーリー数の研究（ Wiki / MathWorld ）、つまり、平面上に規則的な形で配置された点のセットとして表すことができる数に専念します。幾何学的形状：
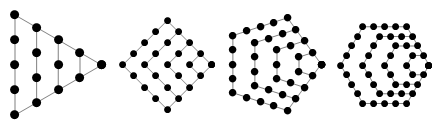
ベルヌーイがいわゆるベルヌーイ数を導入したのはこの部分でした。 彼は二項係数の関係を明らかにすることから始めました
、形式は次のとおりです。
。
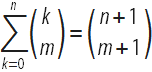[6]で：=
アウト[6] =
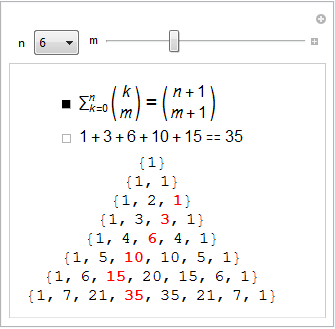
ベルヌーイは、 mの固定値に対して、二項係数
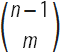変数nの多項式、すなわち 
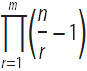。 このアイデンティティにより、彼は自然数の次数の合計の値を導き出すことができました。 
。 彼は0≤m≤10の結果の表を得ました。
ベルヌーイによって取得されたテーブルを再現するために、自然数の次数の合計の方程式を定義する関数を作成します。
[7]で：=
[8]で：=
アウト[8] =
[9]で：=
アウト[9] =
[10]で：=
アウト[10] =
結果の連立方程式を解くと、次のようになります。
[11]で：=
アウト[11] =
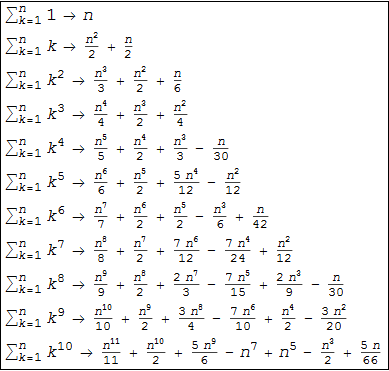
ベルヌーイは、「結果のシーケンスを慎重に研究した人は、追加の計算なしでテーブルをさらに続けることができる」と書いています。
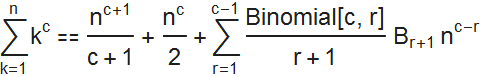
彼はそのオッズ
はnに依存せず、上記の式にn == 1を代入することで再帰的に計算できます。
[12]で：=
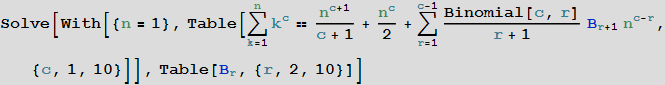
アウト[12] =
これらの係数は、数学の多くの分野で応用されている有名なベルヌーイ数です（たとえば、「 ベルヌーイ数がどこでも発生するのはなぜですか 」の説明を参照してください） 。 （なぜベルヌーイ数がどこにでも現れるのですか？）mathoverflow.net]：
[13]で：=
アウト[13] =
彼の本の第2部では、ベルヌーイは、可能な順列の数、繰り返し要素を持つセットの順列の数、セットから特定のオブジェクトを選択する方法の数などを計算します。 。
3番目の部分では、ベルヌーイは、前の2つの部分で得られた結果を24のギャンブルの問題の解決に適用します。 これらすべてのタスクのライトモチーフは、独立した結果0および1のシーケンスであり、「ベルヌーイプロセス」と呼ばれます。 Jacob Bernoulliの生誕360周年は、Wolfram言語を使用してMathematicaで彼の問題を解決する絶好の機会だと思います。
たとえば、問題9では、3人のプレーヤーのゲームで予想される勝利を見つける必要があります。 プレイヤーは20枚のカードのデッキからカードを交互に（交換も返却もせずに）取り、10枚はカーリーです。 カードがなくなると、よりカーリーなカードを持っているプレイヤーに賞金が均等に分配されます。
c1 、 c2 、およびc3が各プレイヤーのフィギュアカードの数であり、最初のプレイヤーの勝ち分けが次の値に等しいと仮定します。
[14]で：=
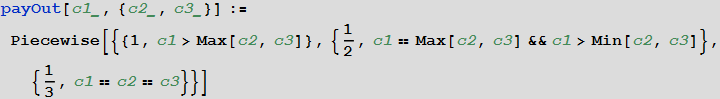
20枚のカードのデッキがプレイヤー間でこのように分配された後、最初と2番目のカードはそれぞれ7枚、3枚目から6枚のカードであるとします。プレイヤー間のカーリーカードの最終的な分配ベクトルは、 MultivariateHypergeometricDistribution関数を備えたWolfram言語：
[15]で：=
[16]で：=
アウト[16] =
[17]で：=
アウト[17] =
このタスクおよび他のタスクは、 添付文書 （英語）で検討および解決されます。
Ars Conjectandi論文の最後の部分では、民事、道徳、および経済の問題に対処する際の確率論の使用について説明します。 この部分では、ベルヌーイは、確率理論は世界の状態に関する不完全な知識を反映していると主張し、ギャンブルとは異なり、いくつかの経験の好ましい結果の数とそれらの可能な合計数の比を見つけることによって確率を決定することができ、「実際の」人生の確率はそうではありません先験的にインストールすることができます。 ベルヌーイは、これらの未知の確率は過去の結果に基づいて計算できると主張しています。
彼は、多数の弱い法則を証明しました。これは、一連のn個の独立した試行で観測される成功率（それぞれの成功確率はp ）は、試行回数を無制限に増やしても無限にpに近づくことを示しています。 したがって、十分な数のテストを行うことにより、任意の精度で確率を推定できます。 したがって、任意のδおよびεに対して 、次のような数n （テストの数）があります。
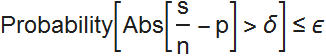
[18]で：=
アウト[18] =
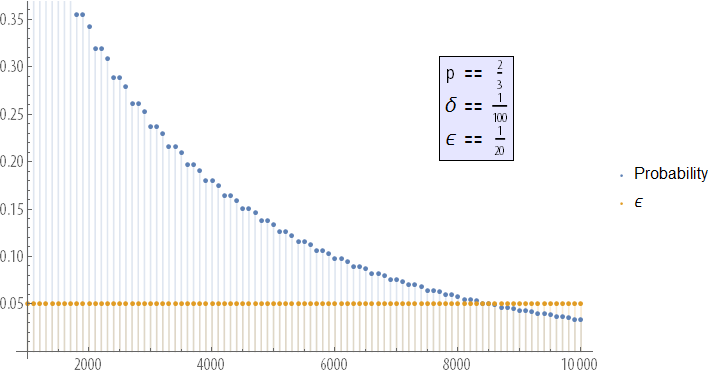
特に、Wolfram Demonstrations ProjectのIan McLeodによるSimed Coin Tossing ExperimentsとLaw of Large Numbersデモは、この収束プロセスを示しています。
ロシア語でWolfram言語（Mathematica）を学習するためのリソース： habrahabr.ru/post/244451