ピアノから始めましょう。 非常に単純化されたこの楽器は、白と黒のキーのセットで、それぞれをクリックすると、低音から高音までの所定の周波数の特定の音が抽出されます。 もちろん、各鍵盤楽器には独自の音色があります。これにより、たとえばアコーディオンとピアノを区別できますが、大まかに言えば、各キーは特定の周波数の正弦波のジェネレーターにすぎません。
ミュージシャンが曲を演奏するとき、彼は交互にまたは同時にキーをつまんで離します。その結果、いくつかの正弦波信号が互いに重なり合ってパターンを形成します。 このパターンが私たちがメロディーだと認識しているのは、さまざまなジャンルのさまざまな楽器で演奏された一曲や、人が無口に口を閉ざしている一曲も簡単に認識できるためです。
ミュージカルドローイングのビジュアルイラスト
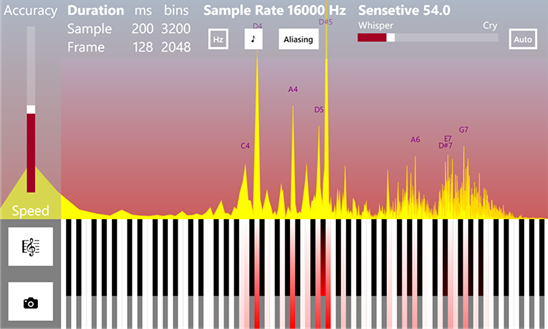
周波数検出(ギターチューナーモード)

逆の問題は、響きのある楽曲を解析して音符にすることです。 つまり、耳で捕捉された音響信号全体を元の正弦波に分解します。 実際、このプロセスは直接フーリエ変換です。 しかし、キーストロークと音声抽出は逆フーリエ変換のプロセスです。
数学的には、最初のケースでは、複雑な(特定の時間間隔での)周期的関数が一連のより基本的な直交関数(サインとコサイン)に分解されます。 そして2つ目は、それらの逆総和、つまり複素信号の合成です。
直交性は、何らかの形で、関数の不混和性を示します。 たとえば、色の付いたプラスチシンをいくつか取り、それらを接着すると、元の色がまだわかりますが、ガッシュ塗料のいくつかの瓶をうまく混ぜると、追加情報なしで元の色を正確に復元することは不可能です。
(!) フーリエ変換を使用して実際の信号を分析する場合、状況を理想化し、現在の時間間隔で周期的であり、基本正弦波で構成されるという仮定から進むことを理解することが重要です。 音響信号は原則として高調波の性質を持っているため、これは多くの場合に当てはまりますが、より複雑な場合が一般的に可能です。 信号の性質についての私たちの仮定は、通常、部分的な歪みとエラーにつながりますが、これがないと、そこから有用な情報を抽出することは非常に困難です。
次に、分析プロセス全体をさらに詳しく説明します。
1.それはすべて、音波がマイクロホンの膜を振動させ、それが電流をアナログ振動に変換するという事実から始まります。
2.次に、デジタル電気信号がサンプリングされます。 この時点で、詳細に停止する価値があります。
アナログ信号は数学的に振幅振幅ポイントの無限の連続セットで構成されているため、測定のプロセスでは、離散時間での有限な一連の値のみを選択できます。つまり、実際には時間量子化を実行します。
原則として、サンプル値は短い等間隔で、つまり16,000または22,000 Hzなどの特定の周波数で取得されます。 ただし、一般的なケースでは、個別の読み取り値が不均一になる可能性がありますが、これは分析の数学的装置を複雑にするため、通常は実際には使用されません。
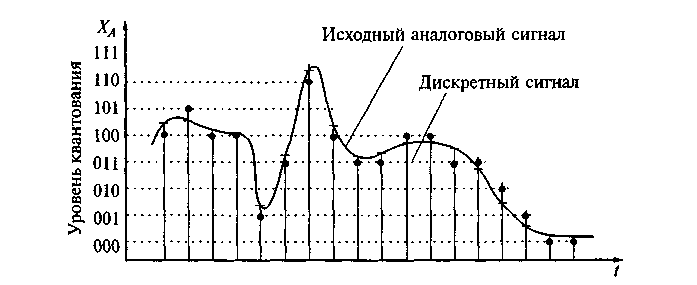
重要なコテルニコフ-ナイキスト-シャノンの定理があります。これは、スペクトルの上限周波数の2倍以上の周波数で採取したサンプルから、有限(幅に制限のある)スペクトルを持つアナログ周期信号を歪みや損失なしで一意に復元できることを示しています(サンプリングレートまたはナイキストと呼ばれます)。
この復元には、特別な補間関数を使用する必要がありますが、問題は、これらの関数を使用する場合、実際には不可能な無限の時間間隔で計算を実行する必要があることです。 したがって、実際には、たとえ最初にコテルニコフ-ナイキスト-シャノンの定理を満たしていても、サンプリングレートを歪みなく人工的に任意に増加させることは不可能です。 この操作には、Farrowフィルターが使用されます。
また、コンピューターは限られた数のセットのみを操作できるため、離散化は時間だけでなく振幅値の観点でも発生します。 また、小さなエラーが発生します。
3.次のステップは、 離散直接フーリエ変換そのものです。
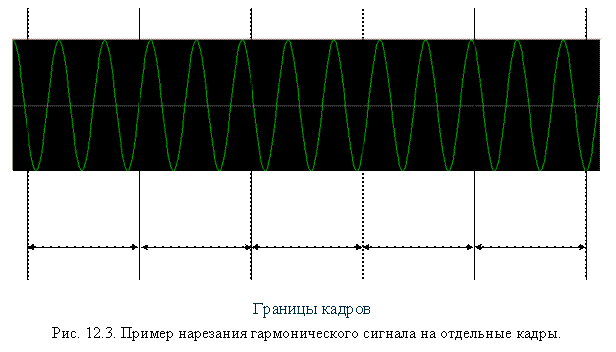
離散サンプルで構成される構成の短いフレーム(間隔)を選択します。これは、従来から周期的と見なされ、フーリエ変換を適用します。 変換の結果として、分析されたフレームの振幅および位相スペクトルに関する情報を含む複素数の配列を取得します。 さらに、スペクトルも(サンプリング周波数)/(サンプル数)に等しいステップで離散的です。 つまり、取得するサンプルが多いほど、周波数の精度が高くなります。 ただし、一定のサンプリング周波数でサンプル数を増やすと、分析される時間間隔が長くなります。実際の音楽作品の音符は音の持続時間が異なり、互いにすばやく置き換えることができるため、重なっているため、長い音符の振幅は短い音符の振幅を「食い」ます。 一方、ギターチューナーの場合、音は通常長く単音に聞こえるので、周波数の解像度を上げるこの方法は良い方法です。
周波数の分解能を上げるためのかなり簡単なトリックもあります。元の離散信号をサンプル間でゼロで埋める必要があります。 ただし、この充填の結果として、位相スペクトルは大きく歪められますが、振幅の分解能は向上します。 Farrowフィルターを使用して、サンプリング周波数を人為的に増やすこともできますが、スペクトルに歪みが生じます。
フレーム期間は通常、約30ミリ秒から1秒です。 短ければ短いほど、解像度は向上しますが、周波数は悪くなりますが、サンプルが長ければ長いほど、周波数は良くなりますが、時間は悪くなります。 これは、量子力学のハイゼンベルグ不確実性原理を非常に連想させます。そして、ウィキペディアが言うように、それは簡単ではありません、数学的な意味での量子力学の不確実性の関係は、フーリエ変換の特性の直接的な結果です...
また、単一の正弦波信号のサンプルを分析した結果、振幅スペクトルが回折パターンに非常に類似していることも興味深いです...
矩形ウィンドウで囲まれた正弦波信号とその「回折」
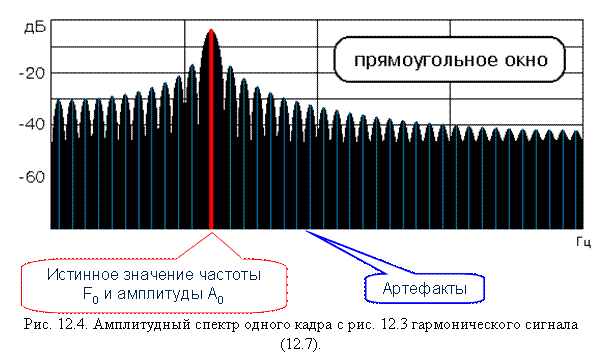
光波回折

実際には、これは信号の分析を複雑にする望ましくない効果であるため、ウィンドウ関数を適用することで信号を低くしようとします。 多くのそのような関数が発明されました、それらのいくつかの実装は、単一の正弦波信号のスペクトルに対する比較効果と同様に、以下に示されます。
ウィンドウ関数を入力フレームに適用するのは非常に簡単です。
for (var i = 0; i < frameSize; i++) { frame[i] *= Window.Gausse(i, frameSize); }
using System; using System.Numerics; namespace Rainbow { public class Window { private const double Q = 0.5; public static double Rectangle(double n, double frameSize) { return 1; } public static double Gausse(double n, double frameSize) { var a = (frameSize - 1)/2; var t = (n - a)/(Q*a); t = t*t; return Math.Exp(-t/2); } public static double Hamming(double n, double frameSize) { return 0.54 - 0.46*Math.Cos((2*Math.PI*n)/(frameSize - 1)); } public static double Hann(double n, double frameSize) { return 0.5*(1 - Math.Cos((2*Math.PI*n)/(frameSize - 1))); } public static double BlackmannHarris(double n, double frameSize) { return 0.35875 - (0.48829*Math.Cos((2*Math.PI*n)/(frameSize - 1))) + (0.14128*Math.Cos((4*Math.PI*n)/(frameSize - 1))) - (0.01168*Math.Cos((4*Math.PI*n)/(frameSize - 1))); } } }

コンピューターに関しては、 高速フーリエ変換用のアルゴリズムが開発されたことがあります。これにより、計算に必要な数学的操作の数が最小限に抑えられます。 アルゴリズムの唯一の要件は、サンプル数が2のべき乗(256、512、1024など)であることです。
以下は、C#での古典的な再帰的実装です。
using System; using System.Numerics; namespace Rainbow { public static class Butterfly { public const double SinglePi = Math.PI; public const double DoublePi = 2*Math.PI; public static Complex[] DecimationInTime(Complex[] frame, bool direct) { if (frame.Length == 1) return frame; var frameHalfSize = frame.Length >> 1; // frame.Length/2 var frameFullSize = frame.Length; var frameOdd = new Complex[frameHalfSize]; var frameEven = new Complex[frameHalfSize]; for (var i = 0; i < frameHalfSize; i++) { var j = i << 1; // i = 2*j; frameOdd[i] = frame[j + 1]; frameEven[i] = frame[j]; } var spectrumOdd = DecimationInTime(frameOdd, direct); var spectrumEven = DecimationInTime(frameEven, direct); var arg = direct ? -DoublePi/frameFullSize : DoublePi/frameFullSize; var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg)); var omega = Complex.One; var spectrum = new Complex[frameFullSize]; for (var j = 0; j < frameHalfSize; j++) { spectrum[j] = spectrumEven[j] + omega*spectrumOdd[j]; spectrum[j + frameHalfSize] = spectrumEven[j] - omega*spectrumOdd[j]; omega *= omegaPowBase; } return spectrum; } public static Complex[] DecimationInFrequency(Complex[] frame, bool direct) { if (frame.Length == 1) return frame; var halfSampleSize = frame.Length >> 1; // frame.Length/2 var fullSampleSize = frame.Length; var arg = direct ? -DoublePi/fullSampleSize : DoublePi/fullSampleSize; var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg)); var omega = Complex.One; var spectrum = new Complex[fullSampleSize]; for (var j = 0; j < halfSampleSize; j++) { spectrum[j] = frame[j] + frame[j + halfSampleSize]; spectrum[j + halfSampleSize] = omega*(frame[j] - frame[j + halfSampleSize]); omega *= omegaPowBase; } var yTop = new Complex[halfSampleSize]; var yBottom = new Complex[halfSampleSize]; for (var i = 0; i < halfSampleSize; i++) { yTop[i] = spectrum[i]; yBottom[i] = spectrum[i + halfSampleSize]; } yTop = DecimationInFrequency(yTop, direct); yBottom = DecimationInFrequency(yBottom, direct); for (var i = 0; i < halfSampleSize; i++) { var j = i << 1; // i = 2*j; spectrum[j] = yTop[i]; spectrum[j + 1] = yBottom[i]; } return spectrum; } } }
FFTアルゴリズムには2つの種類があります。時間と周波数の間引きがありますが、どちらも同じ結果になります。 関数は、時間領域の信号振幅の実数値で満たされた複素数の配列を取り、実行後、振幅と位相スペクトルに関する情報を含む複素数の配列を返します。 複素数の実数部と虚数部は、振幅と位相と同じではないことを思い出してください!
大きさ= Math.Sqrt(x.Real * x.Real + x.Imaginary * x.Imaginary)
phase = Math.Atan2(x.Imaginary、x.Real)
結果として得られる複素数の配列は、ちょうど半分が有用な情報でいっぱいになり、残りの半分は最初のものの鏡像に過ぎず、考慮から安全に除外できます。 考えてみると、この瞬間は、サンプリングレートが最大2倍の信号周波数以上でなければならないというコテルニコフ-ナイキスト-シャノンの定理をよく示しています...
Cooley-Tukey再帰のないFFTアルゴリズムのバリアントもあります 。これは実際によく使用されますが、理解するのが少し難しくなります。
フーリエ変換を計算した直後に、振幅スペクトルを正規化すると便利です。
var spectrum = Butterfly.DecimationInTime(frame, true); for (var i = 0; i < frameSize; i++) { spectrum[i] /= frameSize; }
これにより、サンプルのサイズに関係なく、振幅値の大きさが同じオーダーになることがわかります。
振幅および周波数スペクトルを計算することにより、信号の処理、たとえば周波数フィルタリングの適用や圧縮の実行が簡単になります。 実際、この方法でイコライザーを作成できます:直接フーリエ変換を実行することにより、特定の周波数範囲の振幅を簡単に増減でき、逆フーリエ変換を実行できます(ただし、実際のイコライザーの動作は通常、信号の位相シフトに基づいています)。 また、信号を圧縮するのは非常に簡単です。キーが周波数で、対応する複素数が値である辞書を作成するだけです。 辞書に入力する必要があるのは、信号の振幅が最小しきい値を超える周波数のみです。 耳に聞こえない「静かな」周波数に関する情報は失われますが、許容可能な音質を維持しながら、具体的な圧縮が得られます。 一部には、この原則が多くのコーデックの根底にあります。
4.正確な周波数決定
離散フーリエ変換により、各スペクトル値が周波数の等しい間隔で隣接するものから分離される離散スペクトルが得られます。 そして、信号の周波数が(サンプリング周波数)/(サンプル数)に等しいステップの倍数である場合、顕著な尖ったピークが得られますが、信号周波数が中央に近いステップの境界のどこかにある場合、「カットオフ」ピークを持つピークが得られ、どんな種類の周波数があるのかを言うのは難しいでしょう。 信号に2つの周波数が含まれている可能性があります。 これが周波数分解能の制限です。 低解像度の写真のように、小さな物体はくっついて見分けがつかなくなるため、スペクトルの細部が失われる可能性があります。
しかし、音符の周波数はフーリエ変換ステップのグリッドにはほど遠いため、日常の作業、楽器のチューニング、音符の認識には、正確な周波数を正確に知る必要があります。 さらに、解像度が1024サンプル以下の低オクターブでは、フーリエ周波数グリッドが非常にまれになり、1ステップで数音を合わせることが可能になり、実際にどの音を演奏するかを決定することが事実上不可能になります。
この制限をどうにかして回避するために、例えば放物線のような近似関数が使用されることがあります。
www.ingelec.uns.edu.ar/pds2803/Materiales/Articulos/AnalisisFrecuencial/04205098.pdf
mgasior.web.cern.ch/mgasior/pap/biw2004_poster.pdf
しかし、これらはすべて、一部の指標を改善する一方で、他の指標に歪みを与える可能性のある人為的な手段です。
周波数を正確に決定するより自然な方法はありますか?
はい、それは信号の位相スペクトルの使用に正確に隠されていますが、これはしばしば無視されます。
信号周波数を調整するこの方法は、2つのフレームのスペクトルの位相遅延を計算することに基づいています。
詳細については、リンクをご覧ください。
www.guitarpitchshifter.com/algorithm.html
www.dspdimension.com/admin/pitch-shifting-using-the-ft(+コード例)
eudl.eu/pdf/10.1007/978-3-642-29157-9_43
ctuner.googlecode.com (C ++およびJavaでアルゴリズムを使用する例)
C#では、メソッドの実装は非常に単純に見えます。
using System; using System.Collections.Generic; using System.Linq; using System.Numerics; namespace Rainbow { // Δ∂ωπ public static class Filters { public const double SinglePi = Math.PI; public const double DoublePi = 2*Math.PI; public static Dictionary<double, double> GetJoinedSpectrum( IList<Complex> spectrum0, IList<Complex> spectrum1, double shiftsPerFrame, double sampleRate) { var frameSize = spectrum0.Count; var frameTime = frameSize/sampleRate; var shiftTime = frameTime/shiftsPerFrame; var binToFrequancy = sampleRate/frameSize; var dictionary = new Dictionary<double, double>(); for (var bin = 0; bin < frameSize; bin++) { var omegaExpected = DoublePi*(bin*binToFrequancy); // ω=2πf var omegaActual = (spectrum1[bin].Phase - spectrum0[bin].Phase)/shiftTime; // ω=∂φ/∂t var omegaDelta = Align(omegaActual - omegaExpected, DoublePi); // Δω=(∂ω + π)%2π - π var binDelta = omegaDelta/(DoublePi*binToFrequancy); var frequancyActual = (bin + binDelta)*binToFrequancy; var magnitude = spectrum1[bin].Magnitude + spectrum0[bin].Magnitude; dictionary.Add(frequancyActual, magnitude*(0.5 + Math.Abs(binDelta))); } return dictionary; } public static double Align(double angle, double period) { var qpd = (int) (angle/period); if (qpd >= 0) qpd += qpd & 1; else qpd -= qpd & 1; angle -= period*qpd; return angle; } } }
アプリケーションも簡単です。
var spectrum0 = Butterfly.DecimationInTime(frame0, true); var spectrum1 = Butterfly.DecimationInTime(frame1, true); for (var i = 0; i < frameSize; i++) { spectrum0[i] /= frameSize; spectrum1[i] /= frameSize; } var spectrum = Filters.GetJoinedSpectrum(spectrum0, spectrum1, ShiftsPerFrame, Device.SampleRate);
通常、元のフレームはその長さの1/16または1/32だけシフトされます。つまり、ShiftsPerFrameは16または32です。
その結果、周波数-振幅の辞書を取得します。ここで、周波数値は実数にかなり近くなります。 ただし、それほど顕著ではありませんが、「カットピーク」は依然として観察されます。 この欠点を解消するために、単純に「仕上げる」ことができます。
using System; using System.Collections.Generic; using System.Linq; using System.Numerics; namespace Rainbow { public static class Filters { public static Dictionary<double, double> Antialiasing(Dictionary<double, double> spectrum) { var result = new Dictionary<double, double>(); var data = spectrum.ToList(); for (var j = 0; j < spectrum.Count - 4; j++) { var i = j; var x0 = data[i].Key; var x1 = data[i + 1].Key; var y0 = data[i].Value; var y1 = data[i + 1].Value; var a = (y1 - y0)/(x1 - x0); var b = y0 - a*x0; i += 2; var u0 = data[i].Key; var u1 = data[i + 1].Key; var v0 = data[i].Value; var v1 = data[i + 1].Value; var c = (v1 - v0)/(u1 - u0); var d = v0 - c*u0; var x = (d - b)/(a - c); var y = (a*d - b*c)/(a - c); if (y > y0 && y > y1 && y > v0 && y > v1 && x > x0 && x > x1 && x < u0 && x < u1) { result.Add(x1, y1); result.Add(x, y); } else { result.Add(x1, y1); } } return result; } } }
見込み
音楽作品の音楽分析は、多くの興味深い可能性を開きます。 結局のところ、既製の楽譜を使用できるので、同様のパターンを持つ他の楽曲を検索できます。
たとえば、同じ作品を別の楽器で、異なる方法で、異なる音色で、またはオクターブで移調することができますが、音符は同じままであるため、同じ作品の異なるバージョンを見つけることができます。 「曲を推測する」ゲームを非常に連想させます。
場合によっては、このような分析は音楽作品の盗作を特定するのに役立ちます。 また、楽譜では、理論的には、特定のムードやジャンルの作品を検索することができ、検索を新しいレベルに引き上げます。
まとめ
この記事では、音響信号の周波数を正確に決定し、音符を強調するための基本原則を概説します。 また、離散フーリエ変換と量子物理学との微妙な直観的な関係が示されており、世界の単一の写真での反射を促しています。
PS上記のすべてのコード例を含むRainbow Frameworkは、 Codexからダウンロードできます。
PPSこの記事は、いつかあなたの専門的な活動に役立ち、多くの時間と労力を節約するのに役立つかもしれません。そのため、著者に仕事に感謝したい場合は、寄付をして、アプリケーションを購入 することができます ( 広告付きの無料版 )または、親切な言葉で感謝を表す。
文学
1.音のスペクトル分析の基礎pandia.org/text/77/481/644.php
2. Cooley-Tukeyアルゴリズムwww.codeproject.com/Articles/32172/FFT-Guitar-Tuner
3.オーバーサンプリング(リサンプリング)
www.dsplib.ru/forum/viewtopic.php?f=5&t=11
www.dsplib.ru/content/farrow/farrow.html
4.位相シフトによる周波数補正
www.guitarpitchshifter.com/algorithm.html
www.dspdimension.com/admin/pitch-shifting-using-the-ft(+コード例)
eudl.eu/pdf/10.1007/978-3-642-29157-9_43
ctuner.googlecode.com (C ++およびJavaでアルゴリズムを使用する例)