
インターネット上でさらに検索しても、期待される結果は得られませんでした。非数学者向けの複雑な理論的記述、またはエラーのある理解可能な記述です。
カットの下で、修正されたアルゴリズムとオンライン計算機を待っています。
1963年にカレルのスウィーニーのリトル、マーティによって公開された方法自体は、多くのNP完全問題に適用可能であり、英語と数学の十分な知識がなければ、巡回セールスマンの問題にすぐに適用できない非常に理論化された資料です。
メソッドについて簡単に説明します-これは、明らかに最適ではないソリューションのスクリーニングを伴うすべての可能なオプションの完全な列挙です。
本当に最小限のルートを見つけるためのアルゴリズムを修正
1.各行の最小要素を計算します(行のキャスト定数)
2.各行からその縮小定数を減算することにより、新しいコストマトリックスに渡します。
3.各列の最小要素を計算します(列のキャスト定数)
4.各列からその縮小定数を減算することにより、新しいコストマトリックスに進みます。
その結果、各行と列に少なくとも1つのゼロ要素が含まれるコストマトリックスが作成されます。
5.この段階で、列と行の縮小定数の合計として境界を計算します(この境界は、目的のルートを構築することが不可能なコストよりも低くなります)
1.削減コストマトリックスの各ゼロ要素の不使用に対するペナルティの計算。
マトリックスでインデックス(h、k)の要素を使用しないことのペナルティは、このエッジがルートに含まれないことを意味します。つまり、このエッジを「使用しない」最小コストは行hと列kの最小要素の合計です。
a)与えられた行列内のすべてのゼロ要素を探しています
b)それらのそれぞれについて、不使用に対するペナルティを考慮します。
c)最大ペナルティに対応する要素を選択します(複数ある場合は任意)
2.ここで、セットSを、最大ペナルティ(S w )を持つエッジを含み、このエッジを含まない(S w / o )セットに分割します。
3.これらの各セットに含まれるルートのコスト見積もりの計算。
a)セットS w / oの場合、すべてが単純です:最大ペナルティ(h、k)で対応するエッジを取得しないため、コスト推定値は、セットSのコスト推定値+エッジを使用しない場合のペナルティ(h、k)に等しくなります
b)セットS wのコストを計算するとき、エッジ(h、k)がルートに入るため、エッジ(k、h)がルートに入ることができないため、コストマトリックスにc(k、h)と書く=無限、およびポイントhから「すでに左」にあり、ポイントkに「すでに到着」しているため、hから出ているエッジはなく、kに入っているエッジは使用できないため、クロスコストマトリックス、行hおよび列kから。 その後、マトリックスを提示すると、S wのコスト推定値は、Sとr(h、k)のコスト推定値の合計に等しくなります。ここで、r(h、k)は、変更されたコストマトリックスの縮小定数の合計です。
4. すべての破損していないセットのうち、最小の推定値を持つセットが選択されます。
そのため、費用のマトリックスに1本の線が消されず、1本の列が消されないまで続けます。
小さな最適化-接続ヒューリスティック
はい、本当です、なぜヒューリスティックを導入しませんか? 実際、ブランチとボーダーのアルゴリズムでは、エッジ(h、k)をとるかどうかを決定するノードで実際にツリーを構築し、Sw(h、k)とSw / o(h、k)の2つの子をハングさせます。 ただし、次の反復に最適なオプションは、評価によってのみ選択されます。 それでは、評価だけでなく、ツリーの深さによっても最良のものを選択しましょう。 選択したアイテムが深いほど、カウントの終わりに近くなります。 したがって、最終的に回答を待つことができます。
アルゴリズムは2つの段階で構成されます。
第一段階
コストマトリックスを取得し、ルートrのコストのより低い推定値を計算します。
1.各行の最小要素を計算します(行のキャスト定数)
2.各行からその縮小定数を減算することにより、新しいコストマトリックスに渡します。
3.各列の最小要素を計算します(列のキャスト定数)
4.各列からその縮小定数を減算することにより、新しいコストマトリックスに進みます。
その結果、各行と列に少なくとも1つのゼロ要素が含まれるコストマトリックスが作成されます。
5.この段階で、列と行の縮小定数の合計として境界を計算します(この境界は、目的のルートを構築することが不可能なコストよりも低くなります)
第2(メイン)ステージ
1.削減コストマトリックスの各ゼロ要素の不使用に対するペナルティの計算。
マトリックスでインデックス(h、k)の要素を使用しないことのペナルティは、このエッジがルートに含まれないことを意味します。つまり、このエッジを「使用しない」最小コストは行hと列kの最小要素の合計です。
a)与えられた行列内のすべてのゼロ要素を探しています
b)それらのそれぞれについて、不使用に対するペナルティを考慮します。
c)最大ペナルティに対応する要素を選択します(複数ある場合は任意)
2.ここで、セットSを、最大ペナルティ(S w )を持つエッジを含み、このエッジを含まない(S w / o )セットに分割します。
3.これらの各セットに含まれるルートのコスト見積もりの計算。
a)セットS w / oの場合、すべてが単純です:最大ペナルティ(h、k)で対応するエッジを取得しないため、コスト推定値は、セットSのコスト推定値+エッジを使用しない場合のペナルティ(h、k)に等しくなります
b)セットS wのコストを計算するとき、エッジ(h、k)がルートに入るため、エッジ(k、h)がルートに入ることができないため、コストマトリックスにc(k、h)と書く=無限、およびポイントhから「すでに左」にあり、ポイントkに「すでに到着」しているため、hから出ているエッジはなく、kに入っているエッジは使用できないため、クロスコストマトリックス、行hおよび列kから。 その後、マトリックスを提示すると、S wのコスト推定値は、Sとr(h、k)のコスト推定値の合計に等しくなります。ここで、r(h、k)は、変更されたコストマトリックスの縮小定数の合計です。
4. すべての破損していないセットのうち、最小の推定値を持つセットが選択されます。
そのため、費用のマトリックスに1本の線が消されず、1本の列が消されないまで続けます。
小さな最適化-接続ヒューリスティック
はい、本当です、なぜヒューリスティックを導入しませんか? 実際、ブランチとボーダーのアルゴリズムでは、エッジ(h、k)をとるかどうかを決定するノードで実際にツリーを構築し、Sw(h、k)とSw / o(h、k)の2つの子をハングさせます。 ただし、次の反復に最適なオプションは、評価によってのみ選択されます。 それでは、評価だけでなく、ツリーの深さによっても最良のものを選択しましょう。 選択したアイテムが深いほど、カウントの終わりに近くなります。 したがって、最終的に回答を待つことができます。
さて、実際には、その出版物のエラーについて
ミスは1つだけでした。最後の分割で生じた2つの子からではなく、分割の可能なすべてのパスから最小境界を持つセットを選択する必要があります。
証明
投稿の冒頭の写真に戻りましょう。 

そして、修正されたアルゴリズムを使用したソリューションは次のとおりです。
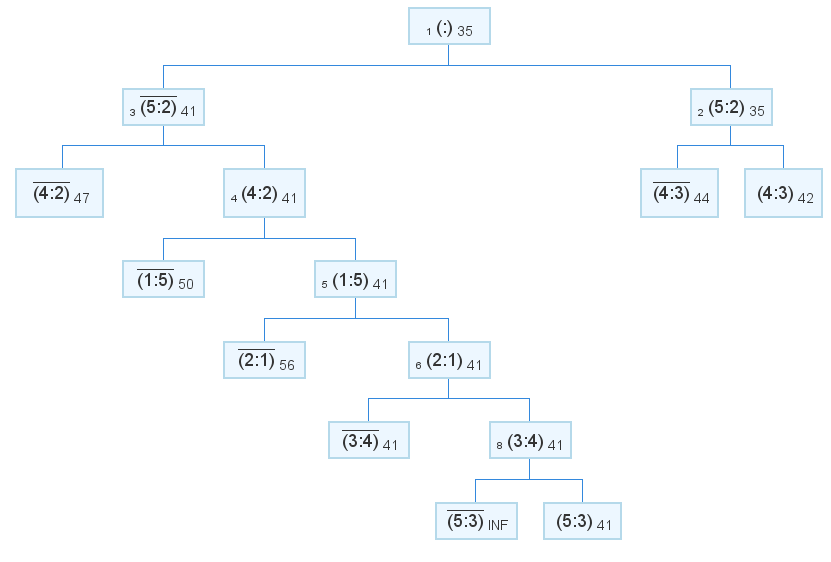
回答:パス:3 => 4 => 2 => 1 => 5 => 3長さ:41
ご覧のとおり、ソリューションに5:2のリブを含めるのは間違いです。 証明するために必要
分岐限定法と5x5から10x10のランダムテーブルに費やされた時間を比較するグラフ:

5x5から66x66のマトリックスに費やされる最大時間と最小時間のスケジュール。

ここで詳細な解決策を試すことができます 。
測定データは100個のランダム行列から取得されました。 あまり良い数ではありませんが、一般的な考え方が提供します。
GitHubのソース(更新済み)。