暗黙的なキーによる永続的なデカルトツリー

注意の持続

今日はかなり珍しい日ですね。 永続的なデータ構造に関する記事がHabréに表示される頻度はどれくらいですか？ そして今日は、暗黙のキーによって、不当に忘れられた永続的なデラミドについてお話したいと思います。 それでは始めましょう。

1.著者は永続性とはどういう意味ですか？

情報源によると、永続データ構造は、変更操作が発生したときに以前のバージョンすべてに関する情報を保存するデータ構造です。

データ構造を永続化する方法にはいくつかのオプションがあります。 この場合、何かが変更された頂点のみをコピーすることにより、完全に永続的なデータ構造を作成します。 したがって、通常のデラミドの構造を何らかの形で変更したり、変更を加えてツリー全体を完全にコピーしたりする必要はありません。 いいですか もちろん！

2.これを行う方法

通常の暗黙の重要なデラミド構造を考慮してください。 根拠がないように、セグメントの金額を考慮します。

struct PersistentTreap { int size; long long sum, key; PersistentTreap *left, *right; //     PersistentTreap() { left = NULL; right = NULL; key = sum = 0; size = 0; } PersistentTreap(int x) { left = right = NULL; sum = key = x; size = 1; link = 0; } //      }; typedef PersistentTreap* PtrPersistentTreap; int getSize(PtrPersistentTreap root) { if (!root) return 0; return root->size; } long long getSum(PtrPersistentTreap root) { if (!root) return 0; return root->sum; } void addLink(PtrPersistentTreap root) { if (!root) return; root->link++; } void update(PtrPersistentTreap root) { if (!root) return; root->size = 1 + getSize(root->left) + getSize(root->right); root->sum = root->key + getSum(root->left) + getSum(root->right); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、これはコードのかなり些細な部分であり、暗黙のキーによって少なくとも一度はデラミドを書いたすべての人に知られています。 次に、最も興味深いものに移ります：操作が（オプションとして）分割、マージ、およびプッシュされて、ツリー構造が不可逆的に変更されないようにする方法

これを理解するのに役立ついくつかの写真を検討してください。

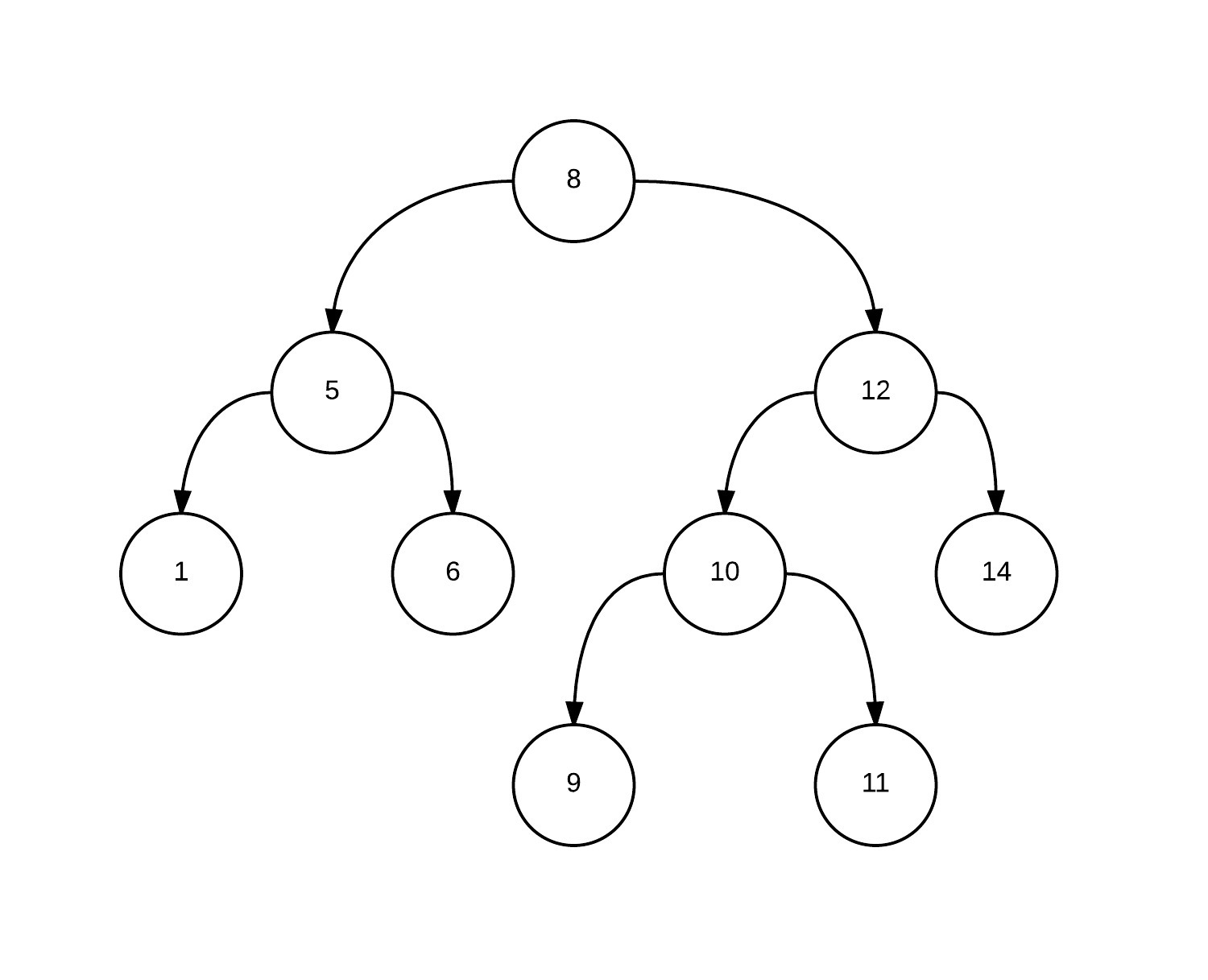
分割操作前の元のデカルトツリー。 （頂点は、配列内の頂点に対応する数字です）。 つまり、配列に似ています 。





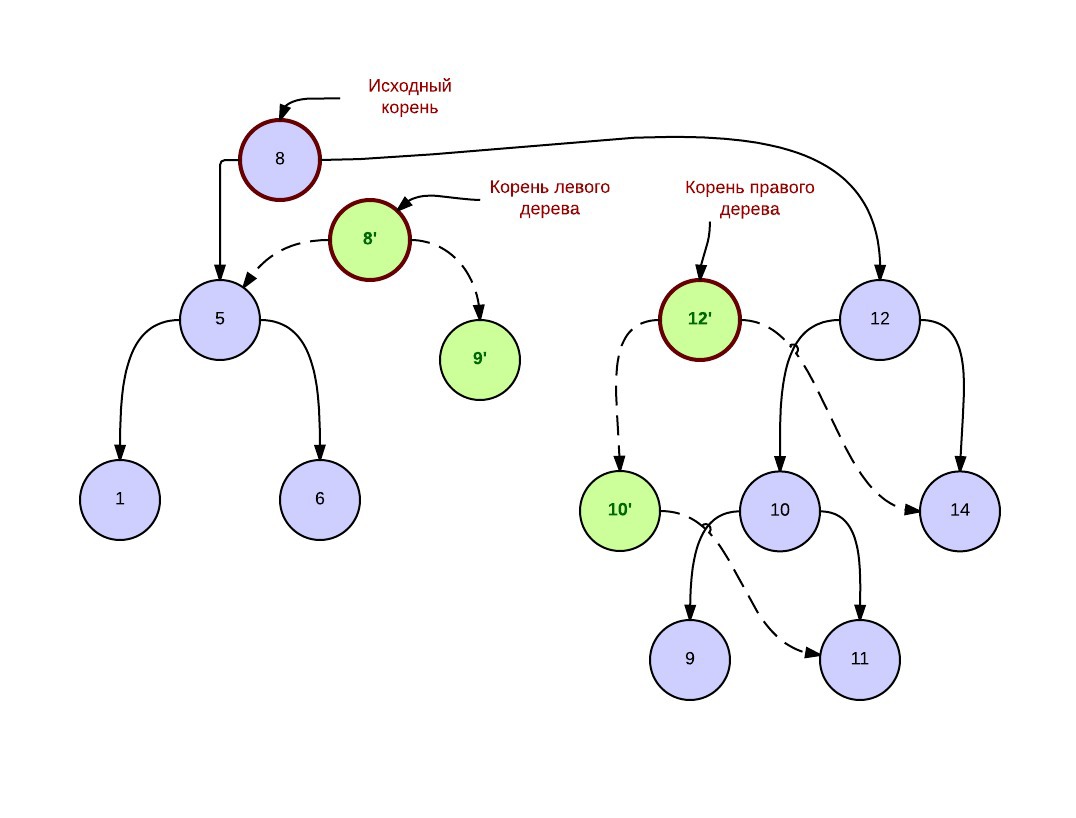
右側のツリーで5つの要素を要求した永続的な分割操作の後、次のフォレストを取得します。 青は元のデラミドの頂点を示し、緑は新しい頂点を作成しました。 点線の矢印は、新しい頂点間の接続を示します。





そのため、分割操作を再帰的に呼び出すたびに、既存のツリーを修正する権利はありません。この頂点のコピーである新しい頂点を作成し、それだけですべての変更操作を実行する必要があります。 文字通り、これは私たちが書くものです。 これを行うには、まずコピーコンストラクターを作成します。

 PersistentTreap(PersistentTreap* cur) { if (!cur) { return; } left = cur->left; right = cur->right; sum = cur->sum; key = cur->key; size = cur->size; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、分割操作の永続バージョンを作成できるようになりました。 通常のものとの唯一の違いは、変更したいルートを単純にコピーし、通常の作業を続行することです。

 void Split(PtrPersistentTreap root, PtrPersistentTreap &L, PtrPersistentTreap &R, int size) { if (!root) { L = R = NULL; return; } PtrPersistentTreap cur = new PersistentTreap(root); if (getSize(cur->left) + 1 <= size) { split(cur->right, cur->right, R, size - getSize(cur->left) - 1); L = cur; } else { split(cur->left, L, cur->left, size); R = cur; } update(L); update(R); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべての作業の3分の1が完了しました。 ここで、永続的な操作のマージに対処する必要があります。 何らかの方法で取得された2つのデラミドを考えます（ここでも、すべてが元の配列から取得されていると考えてください）。 マージ操作が正しく機能するように、それらの優先順位を割り当てて、最大値がルートにあるようにします（括弧内に赤で強調表示されます）。 後でアルゴリズムが適切に機能するために実際には必要ないことが示されます。





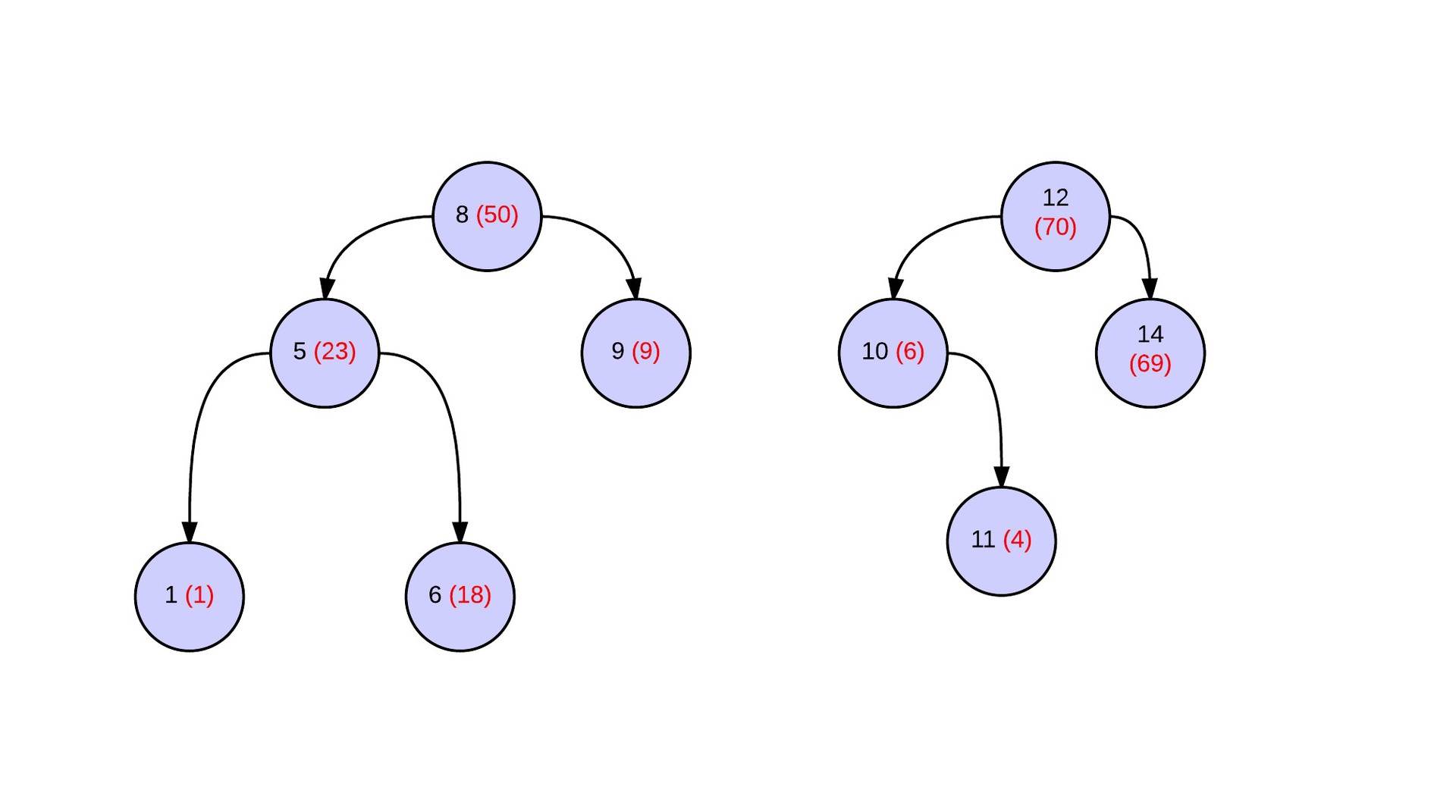
マージ操作の結果は、頂点の優先順位に対してヒーププロパティが実行されるデラミドです。 以下は、マージ操作後のツリーの写真です。 青は元のデラミドの頂点を示し、緑は新しい頂点を作成しました。 点線の矢印は、新しい頂点間の接続を示します。



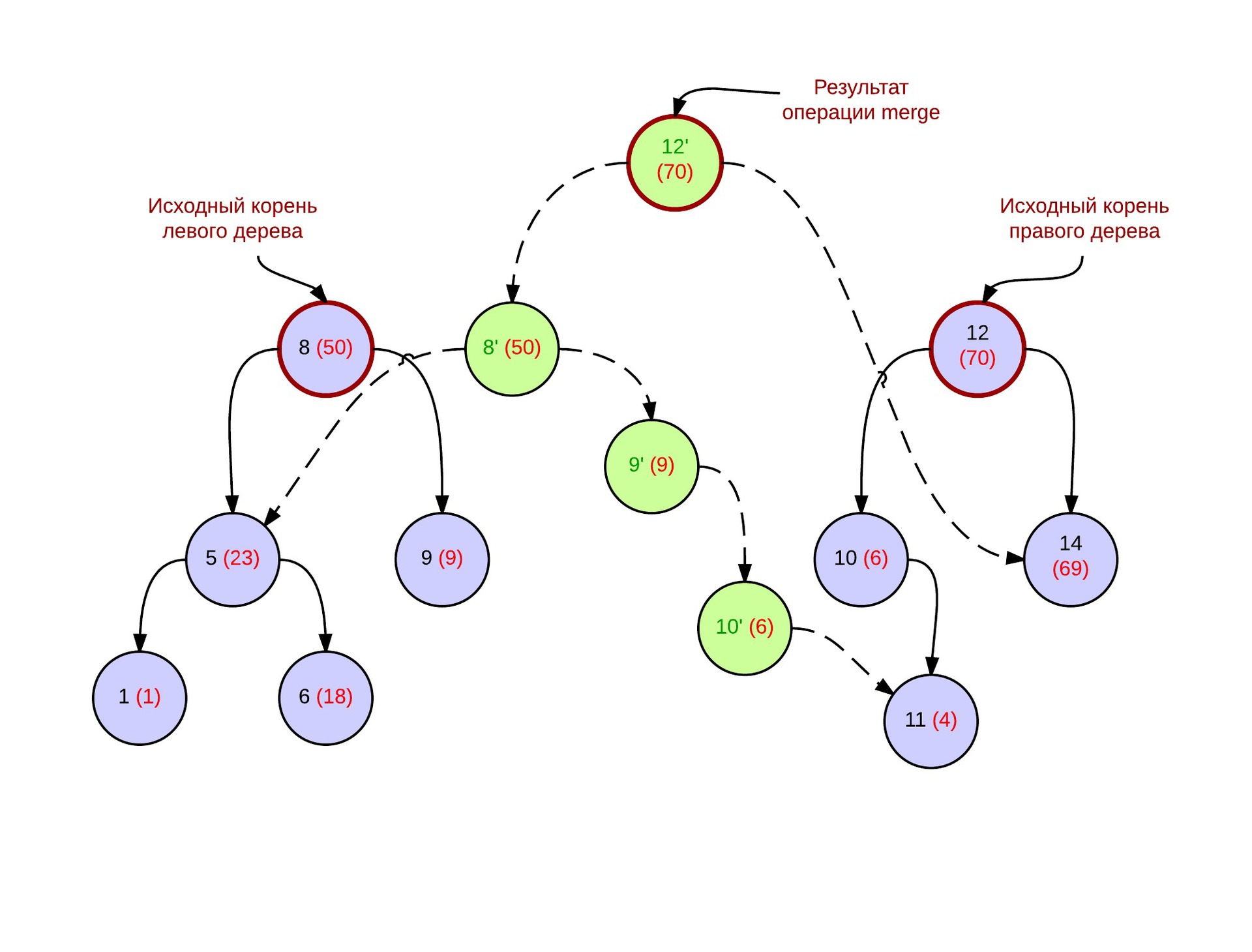
実装では、新しいツリートップへのポインタを返すためにマージが必要になります。 したがって、各呼び出しで、ルートになる頂点をコピーし、彼女のポインタを息子の1人に変更します。 どちらが左の木か右の木かによって異なります。

 PtrPersistentTreap Merge(PtrPersistentTreap L, PtrPersistentTreap R) { PtrPersistentTreap ptrNode = NULL; if (!L || !R) { ptrNode = new PersistentTreap((!L ? R : L)); return ptrNode; } if (L->prior > R->prior) { ptrNode = new PersistentTreap(L); ptrNode->right = Merge(L->right, R); update(ptrNode); return ptrNode; } else { ptrNode = new PersistentTreap(R); ptrNode->left = Merge(L, R->left); return ptrNode; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ただし、頂点ではフィールド全体を事前に保存する必要はまったくないことが約束されていましたが、今ではそれを取り除く方法を説明します（永続的な実装に非常に便利です）。 実際、優先順位が一致する場合、ツリーは通常の竹に縮退する可能性があり、その利点はすぐにゼロになります。 最上位への呼び出しごとに新しい優先度を設定することは、他とまったく一致しないという事実や、ツリーの構造が保持されるという事実ではなく、高価な喜びです。 シンプルでエレガントなソリューションがあることがわかりました。



デラミドの各頂点は、それが表すツリーのサイズで格納します。 したがって、この値を使用すると、頂点の優先度を接続してルートになることができます。 より大きなツリーを持つ頂点の優先度がより高くなることを保証するのに十分論理的です。 この場合、各頂点が木の根になる確率が同じであることを証明しましょう。 これは帰納法で行います。 2つの頂点のルートを選択してみましょう。 明らかに、それらのルートになる確率は等しくなります。 ここで、左側のツリーにL個の頂点、右側のツリーにR.だけがある場合を考えます。その後、アルゴリズムに従って、左側のツリーの頂点が確率でルートになることができます 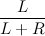。 しかし、ツリーLの頂点の各頂点は、確率でルートになる可能性があります 。 したがって、ツリーLの各頂点は確率付きで根になることができます 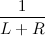。 右側のツリーの場合も同様に考慮されます。 それだけです。すべての頂点の確率が同じなので、遷移が証明されます。

そのため、代わりにマージ操作で

 if (L->prior > R->prior)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

書ける

 int l = getSize(L), r = getSize(R), rang = rand() % (l + r); if (rang > r)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、何も変わりません。

3.上部に参照カウントを追加します。

永続的なデータ構造の大部分が書き込まれます。 次に行う必要がある変更は、参照カウントの実装です。 これを行うには、このフィールドを参照する頂点の数を格納するリンクフィールドを追加する価値があります。 このフィールドが空でない場合、ツリーの残りのバージョンに何らかの影響を与えるため、現在の頂点を削除することは決してできないと考えるのが論理的です。 そして、はい、頂点を削除するとき、その子のリンクも削減し、必要に応じて再帰的な削除を行います。



これで、暗黙のキーを使用して永続的なデラミドを最終的に記述したと言うことができます。 なぜ必要なのですか？ 通常の暗黙的なキーderamideとまったく同じ操作を実行できますが、それとは異なり、優先順位を一致させたり、deramideの完全なコピーとの通信時間を長くしたりすることなく、配列の一部をコピーし、配列の一部のコピーを配列に貼り付けることができます。 持続性デラミドの使用例 。