計算された知識と純粋数学の未来

スティーブン・ウルフラムによる計算知識の翻訳と純粋数学の未来

この翻訳を手伝ってくれた人々に深く感謝します。ヴラディスラフ・グラゴレフ（ ヒムラ ）、 イリヤ・マルチェフスキー 、セルゲイ・シェフチュク（ opckSheff ）、 アンナ・ コバレンコ 。

はじめに

1世紀以上にわたり、4年ごとに、世界のある時点で、国際数学者会議（ICM）が開催されます。 1900年、デビッドヒルバートが有名な数学の問題のコレクションを発表し、今日に至るまで世界中の数学者の研究の方向性を定めています。



今年、 ICMはソウルで開催され、今日はソウルに行きます。 1990年に京都でICMに参加したことがあります。 それからMathematicaはわずか2歳で、数学者はそれに慣れ始めたばかりでした。 多くの人がすでにそれをどこでも使っていますが、ICMには、「私は純粋な数学をやっています。 おもしろいことに、 Mathematicaで何ができますか？」







24年後、世界中の純粋数学の分野のほとんどの専門家が、何らかの形でMathematicaシステムを使用しています。 しかし、それにもかかわらず、多くの純粋な数学者は、何世紀にもわたって正確に-手と紙ですべてをし続けています。



1990年にICM議会に出席して以来、この伝統的なプロセスにテクノロジーをどのように組み込むことができるかについて考えることを止めていません。 そして今、どういうことかを話したいと思っています。 注意する必要があります：多くの詳細はまだ私には不明です。 しかし、計画を実行するためには、世界中のほとんどの純粋な数学者の支援と協力が必要です。 すべてがうまくいった場合-結果は印象的であることが約束されます-Mathematicaシステム（および若い世代のWolfram | Alpha）がすべての計算数学を変更したのと同じくらい確実に純粋な数学者に作業方法を変更させます。 潜在的に、この結果は純粋な数学を新しい黄金時代に導く可能性があります。

純粋な数学ワークフロー

一般に、この問題は非常に複雑です。 しかし、私にとって最も重要な出発点の1つは、計算数学と純粋数学で使用される方法の違いです。 計算数学では、通常、特定の計算上の問題が提起され、通常の数学の作業セッションと同様に、結果を得るために解決されます。 純粋な数学では、逆に、いくつかの数学的なオブジェクト、結果または構造が取られ、それらに関していくつかの仮説が形成され、次に仮説の妥当性の証明が提示されます。



このようなワークフローにテクノロジーを効果的に導入するにはどうすればよいですか？ 1つの簡単な方法があります-Wolfram | Alphaを考えてください。 2 + 2を入力すると、Wolfram | AlphaはMathematicaと同じように4の応答を返します。しかし、「 new york 」、「 2.3363636 」、または「 cos（x）log（x） 」と入力すると、それから数えられない単純な「答え」。 代わりに、Wolfram | Alphaは、入力したデータに関する一連の「興味深い事実」を含むレポートを生成します。







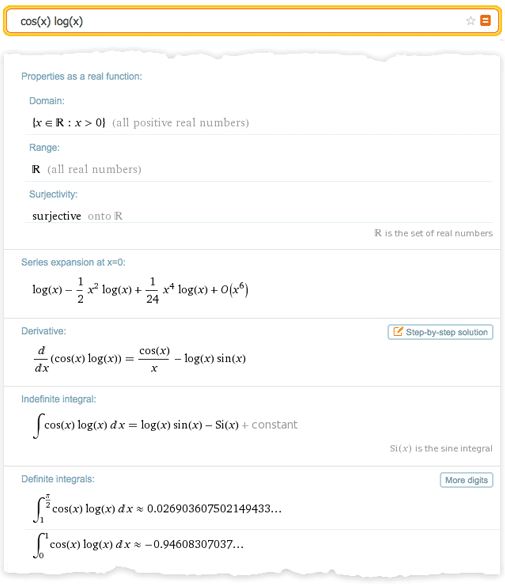
この種の答えは、純粋な数学のワークフローに完全に適合します。 数学的なオブジェクト、結果、または構造を入力すると、非常に賢明な数学者の同僚ができるように、システムはそれらについて何かを伝えようとします。 必要に応じて、知りたいことを正確にシステムに伝えることができます。または、真実である可能性のあるステートメントを示すことさえできます。 しかし、Wolfram | Alphaで働くことは、「これについて何を教えてもらえますか？」などの質問に対する答えを見つけるようなものです。Mathematicaでは、「私が尋ねたものに対する答えは何ですか？」



Wolfram | Alphaは、あらゆる種類の数学オブジェクトで既に多くのことを行うことができます。 たとえば、 数値 、 数式 、 グラフ 、 確率分布などを入力すると、Wolfram | Alphaは洗練されたアルゴリズムを使用して、入力されたデータに関する詳細なレポートを詳細なレポートの形式で作成します。







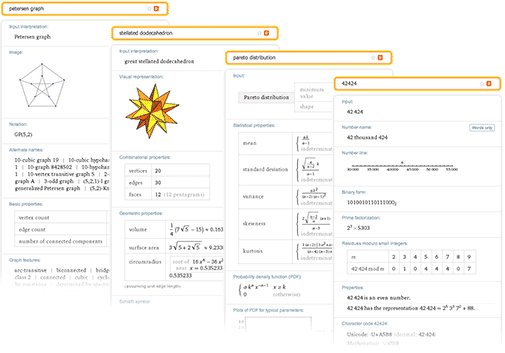
しかし、純粋な数学を扱うときに実際に役立つようにするには、Wolfram | Alphaシステムに何か他のものが必要です。 特定の数学的オブジェクトを操作することに加えて、抽象的な数学的構造を操作する能力も必要です。



純粋な数学の無数の記事は、「Fはそのような性質を持つフィールドだと仮定してください」という言葉で始まります。 したがって、後からシステムがフィールドFに関する定理と事実を自動的に提供し、本質的に、フィールドFに関する本格的な記事を個別に作成できるように、類似のものを導入できる必要があります。



それでは、このようなシステムを作成するには何が必要ですか？ 原則として作成することは可能ですか？ そのようなシステムに必要ないくつかのコンポーネントがあります-それらは複雑であり、それらを作成するのに多くの時間がかかります。 しかし、 Mathematica 、Wolfram | Alpha、 A New Kind of Science （セルオートマトンと関連トピックに関する基本的なモノグラフは「 A New Kind of Science 」です）での経験に基づいて、正しいガイダンスと十分な努力で、すべてができると確信しています作成されました。



重要なコンポーネントは、数学的な概念と構造の正確な記号記述の可用性です。 Mathematicaシステムには、その四半世紀以上にわたる研究の結果、ほとんどがすでに存在しています。 したがって、 Wolfram言語は幾何学的なオブジェクト 、 方程式 、 確率過程 、 数量詞などを表現する最も抽象的な方法を直接統合します。しかし、Wolfram言語がこれまで持っていないのは、例えば全単射、抽象半群、デカルト平方などの純粋な数学の概念の表現です。

Mathematicaプラ

何世紀にもわたって、多くの数学者がさまざまな問題を研究してきました。 しかし、Wolfram言語を拡張して純粋な数学の問題の全範囲をカバーし、「Mathematica Pura」のようなことをすることは可能でしょうか？ 間違いなく、答えはイエスです。 この問題を解決することは驚くほど興味深いでしょうが、言語の構造の複雑な研究​​が必要になります。



私は35年間このような言語の構造を開発してきました。これは私がこれまでに遭遇した中で最も難しい知的作業であると言えます。 明確な思考と審美的で実用的なアプローチの組み合わせが必要です。 物事の最も深い理解を達成し、可能な限りすべてを統一するために、常にそれを把握する必要がありますが、作業の結果は常に、物事を最も簡単で明白な方法で表すプリミティブでなければなりません。



現時点では、純粋な数学（たとえば記事）を記述する主な方法は、 数少ない表記法に加えて 、 数学表記と自然言語の混合です。 そして、それは、純粋な数学のための正確な記号言語を開発するときの出発点であるべきです。



何らかの方法で数学表記がすでにこの問題を解決していると思うかもしれませんが、実際には、数学表記を使用して標準化された方法で表現できる構造や概念はそれほど多くありません。それらはすでにWolfram言語で利用可能です。



それでは、さらに先に進むにはどうすればよいでしょうか？ 最初のステップは、必要なプリミティブを理解することです。 Wolfram言語全体には現在、約5,000個の組み込み関数と何百万もの組み込み標準化データオブジェクトが含まれています。 純粋な数学を幅広くサポートするには、おそらく数万の新しいデータオブジェクトまたは既存の構造を補完しリンクする類似物とともに、約1,000の追加の機能が必要になると思われます。







関数空間などのドメインを検討してください。 おそらく、この領域には、関数空間を定義するFunctionSpace関数があるはずです。 次に、関数スペースでの操作が必要になります。たとえば、PushForward（マッピングのアクションの下でイメージを測定）またはMetrizableQ（計量可能なスペースかどうか）です。 次に、「CInfinity」（無限微分可能関数の空間）など、さまざまなパラメーター化オプションを使用して、多くの既知の関数空間を定義する必要があります。



低レベルでは、シンボリック式になります。 しかし、Wolfram言語では、最終的に情報を直接入力する3つの方法があります。これらはすべて、便利で読みやすい言語を得るために必要です。 最初の方法は、 +やasなどの短い表記を使用することです。これは、通常の数学表記とまったく同じです。 2番目は、 MatrixRankやSimplexなどの非常に複雑な関数名の使用です。 3番目は、自然言語での自由形式の入力の使用です。たとえば、「trefoil knot 」（トレフォイルノット）または「 aleph0 」（aleph-0セットのカーディナリティ）です。



最も一般的な構造要素または接続要素のいくつかについて短い記録が必要ですが、適切な量が必要です。少なすぎず（LISPのように）、多すぎないように（APLのように）。 また、関数の名前を、単に普通の単語で記述されているようにしたいので、単語から名前を読み取るだけで関数の目的を簡単に把握できます。

コンピューターと人々

しかし、Wolfram言語の現代世界では、自然言語の自由形式の入力もあります。 ここでのキーポイントは、それを使用すると、実際の数学者だけが理解して使用する便利な（いものの）さまざまな記録オプションを効果的に使用できることです。 たとえば、「L2」は、対応するコンテキストでは「2次のルベーグ空間」と解釈できます。 自然言語認識システムは、そのようなリクエストの解釈のあいまいさを解決し、そのための標準的なシンボリックフォームを見つけるように注意します。



最終的に、独自の名前を持つ純粋な数学の各デザインまたは概念は、シンボリック言語でその場所を見つける必要があります。数学者が名前を聞くとすぐに理解する、あらゆる分野の本質。



純粋な数学の概念で機能する正確なシンボリック言語を作成できるとします。 それで何ができますか？



「Wolfram | Alphaスタイル」で作業できるとしましょう。自由形式で何かを入力すると、入力されたデータは言語によって解釈され、すべての計算が完了すると、生成されたレポートを受け取ります。



しかし、このオプションを検討することもできます。完全に考え抜かれたシンボリック言語があれば、コンピューターだけでなく人間にも役立ちます。 実際、言語が十分に優れていることが判明した場合、人々はおそらく、自然言語と数学表記の古典的な混合物ではなく、その上で数学計算を書き留め始めるでしょう。



Wolfram言語でプログラムを作成するとき、かなり頻繁にそれについて直接考えることが判明します。 私は自然言語でこれからWolfram言語に翻訳することでやりたいことを思いつきません。 Wolfram言語で最初に思考を形成し、その構造はこれらの思考を形成するのに役立ちます。



純粋数学のために十分に優れた記号言語を開発できれば、これはとりわけ、数学者に思考に直接使用できるツールを提供します。 正確なシンボリック言語で自分の考えを説明できれば、あいまいさやあいまいさの可能性がないため、これも良いことです。言語のドキュメントでは、オブジェクトやシンボルのあいまいでない説明を常に見つけることができます。



同時に、純粋な数学が正確な記号言語で書き出されるとすぐに、計算ができるようになります。 証拠を生成して検証できます。 定理を検索できます。 関係と前提条件チェーンを自動的に見つけることができます。



しかし、まあ、純粋な数学に必要なコンピューティングデバイスがあるだけだとしましょう。 「Wolfram | Alpha-style」ワークフローを実装するためにそれをどのように使用できますか-物事の説明を入力し、それらに関するあらゆる種類の数学的知識を自動的に取得する場合



この問題を解決するには、明らかに2つの異なる方法があります。 1つ目は、入力されたデータの可能な定理の抽象的なリストを提示し、その後、発見的アルゴリズムを使用して興味深い可能性のある定理を選択することです。 2つ目は、数学の文献でこれまでに公開された数百万の定理の計算されたバージョンを作成することから始め、次にそれらと任意の入力クエリの間の接続を見つける方法を理解することです。



実際、これらの各領域は、数学の分野で研究がどのように行われるかについてのわずかに異なる見解を反映しています。 そして、それぞれの方向について伝えるべきことがあります。

列挙による数学

定理のシーケンスから始めましょう。 最も単純な場合、公理のシステムと、このシステムに基づく真の定理の一貫した定式化から始めることができます。 これを行うには、主に2つの方法があります。 1つ目は、架空のステートメントを作成し、 直接または間接的な証拠を使用して、真のステートメントを決定することです。 2番目は、証明の可能な方法をリストし、公理を使用する可能な方法を見つけ出すことです。



オブジェクトがブール代数などの場合、両方のメソッドは簡単に実装できます。 結果は、一連の真の定理になります。 しかし、人がそれらを見ると、それらの多くは些細な、または面白くないように見えます。 したがって、どの定理が生成されたレポートに含まれるのに「十分興味深い」かという疑問が生じます。



私の最初の仮定は、この問題に対するこのような自動アプローチは存在せず、さまざまな定理への関心は、対応する数学分野の歴史的発展に必ず依存するというものでした。 しかし、新しい種類の科学に取り組んでいたとき、ブール代数で簡単な実験をしました。







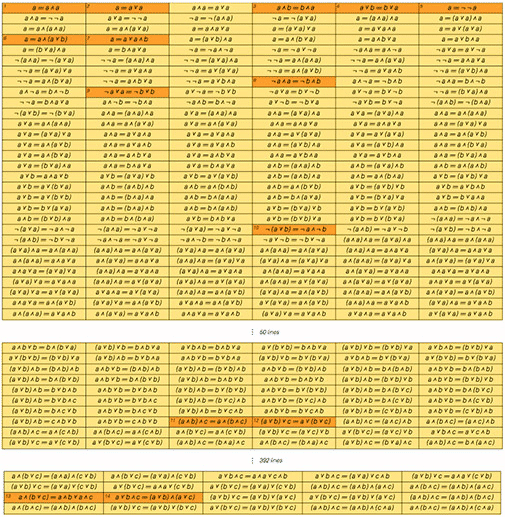
ブール代数には14の定理があり、「非常に興味深い」と見なされ、教科書で特別な名前が付けられています。 すべての可能な定理を取り、複雑な順序で（変数、演算子などの数で）リストしました。驚くべきことを見つけました-上記の定理の全体は、主にリストの前のものを使用して直接証明できないものに適用されます。 言い換えれば、名前が与えられた定理は、ある意味、ブール代数に関する新しい情報を与える最小限のステートメントです。



もちろん、ブール代数は最も単純な例です。 さらに、この構成例では、すべての公理に対応する定理を取得するとすぐに、多くの数学理論にとって不合理な「興味深い」定理はもうないと結論付けることができます。 しかし、この例は、どの定理を「レポートに含める」べきで、どの定理が「面白くない」レポートの単なる「装飾」であるかを実際に自動的に見つける方法をよく示していると思います。

興味の尺度

もちろん、関心の分類の問題はWolfram | Alphaで常に発生します。 数学的な例では、「グラフのどの領域が最も興味深いか」、「式のどの代替形式が興味深いか」などの質問です。誰かが単一の数字を入力しても、「この数字のどの閉じた形式が面白いですか？」 -そして、これを理解するためには、あらゆる種類の数学的オブジェクトを分類する必要があります（たとえば、 対数（343）やKhinchin定数などに対するπの表現はどのくらい複雑ですか？）







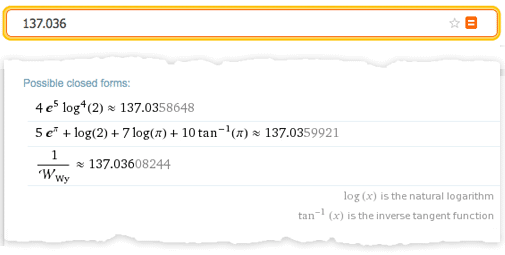
したがって、原則として、入力に含まれるものについて「興味深い」定理を生成するシステムを想像できます。 Mathematicaの通常の計算では、データが入力され、「答えを得るために計算」が実行されますが、ここでは興味深いステートメントが生成されます。



入力の性質も異なります。 計算の場合、通常、実行する必要がある操作を処理します。 「Wolfram | Alphaスタイル」で純粋な数学を扱う場合、ユーザーは通常、オブジェクトの説明を提供します。 場合によっては、明示的です。たとえば、特定のタイプの数、特定の方程式、特定のタイプのグラフなどです。 しかし、多くの場合、暗黙的なものであり、たとえば、一連の制限にすぎない場合があります。 前述のフィールドの例では、「Fをフィールドにする」と言ってから、このフィールドが満たすべき制限を設定します。



ある意味で、公理体系は制限も設定します 。そのような演算子は「ナンド」（シェーファーのストローク）であるとは述べていません。 オペレーターは特定の条件を満たす必要があると単純に述べられています。 ゲーデルの定理から、Peanoの標準的な算術のようなものでさえ、制限を完全に克服することは不可能であることがわかります。たとえば、整数の単純な加算など、公理の+記号に特定の演算を割り当てることはできません もちろん、そうすることで、レポートに使用するものを含め、「+」に関するかなりの数の定理を証明できます。



したがって、特定の入力を使用して、それらを正確なシンボリック言語の制約のセットとして表現する方法を見つけることができます。 次に、これらの制限に基づいて定理を定式化し、それらから「最も興味深い」ものを発見的に選択します。



いつかこのレッスンが純粋な数学者の仕事の最も重要な部分になると確信しています。 今日、ほとんどの純粋な数学者にとって、このタスクは「作者なし」の定理に慣れていないため、異質に思えます。 それらは特定の数学者の記事からの定理に使用されます。



そして、これが「数学的な知識の自動生成への第2のアプローチにつながります。書かれた数学的な記事のコレクション全体から始めて、それを特定の入力と関連付けます。 たとえば、「記事Xの次の定理は、何らかの形で入力に適用できます」などと言えます。

数学データベース全体の監督

数学の歴史的基盤はどのくらいですか？ 出版された数学記事は約300万、つまり約1億ページあり、この数は年間平均200万ページ増加しています。 さらに、これらのすべての記事では、明らかに約500万の異なる定理が含まれています。



このすべてで何ができますか？ まず、もちろん、単純な調査と処理。 多くの場合、記事の単語には、単なる数学表記や定理の記述よりもはるかに多くの資料が記載されています。 しかし、Wolfram | Alphaの数学的クエリのための言語認識技術の助けを借りて、数学的記事のストックの優れた統計処理を実行することはそれほど難しくありません。



しかし、さらに先へ進むことは可能ですか？ 可視性を向上させるために、ソースドキュメントのタグを作成することを検討する人がいるかもしれません。 しかし、インターネットでは各ドキュメントとそのグループからタグを追加するよりも、より洗練された情報に基づいたシステムを作成する方がはるかに簡単で優れているという事実が示すように、このような作業は意味をなさないと考えています



確かにより合理的であるのは、定理を元の計算可能な形式に翻訳することです：記事から定理を抽出し、それらを正確な記号言語で書き直します。



これを自動的に行うことは可能ですか？ 最終的には、ほとんどの部分で可能になると思います。 今日、私たちはすでに記事から定理の小さな断片を取り出し、 Wolfram | Alpha 言語認識システムを使用してそれらをWolfram言語コードに変換することができます。 しかし、徐々に大きな断片に進むことが可能になり、最終的に、典型的な定理を正確な記号形式に変換するには、人の最も取るに足らない努力だけが必要であるという結論に達します。



したがって、数学文献からのすべての定理を計算可能な形式で整理したとしましょう。 次に何をしますか？ もちろん、Wolfram | Alphaに似た視覚システムを構築することもできます。これは、純粋な数学の実践に非常に役立ちます。

不溶性の問題

ただし、実際には数学自体によって課せられるいくつかの制限が避けられません。 たとえば、どの定理をどのオブジェクトに適用でき、どの定理が同等であるかを言うのは必ずしも容易ではありません。 最後に、これらは古典的な理論的に不溶性の問題であり、実際に問題を引き起こすと思われます。 少なくとも、彼らは自動証明などの基本的なプロセスを適用できます。



したがって、ここで説明した2つの主なアプローチの組み合わせが提案されています。 最初に、公開された数学的著作物の資金全体を取り、公式に500万の巨大な公理系とみなし、その後、定理の連続的な声明、つまり「興味深い事実のリスト」と呼ばれるものの手順に従います。

数学：科学か芸術か？

それで、そのようなシステムを作成したとしましょう。 彼女は純粋な数学で新しい真実を見つけるという重要な課題を本当に解決するのでしょうか、それとも彼女はこれに対処しないのでしょうか？



それはすべて、純粋数学の本質と考えられるものに依存していると思います。 それは科学ですか、それとも芸術ですか？ これが科学である場合、より多くの定理をすばやく作成することは確かに非常に優れています。 しかし、それが芸術であれば、これは主なものではありません。 純粋な数学の仕事を芸術的な絵で考えると、このアプローチの基礎は人の自己表現の形であるため、自動アプローチは逆効果になる可能性が高くなります。



同じことが証拠の役割にも当てはまります。 一部の数学者にとっては、定理のみが重要です：声明が真実かどうかを知ること。 実際、証拠はエラーがないという事実だけです。 しかし、他の数学者にとって、証明は数学の内容の重要な部分です。 彼らにとって、証明は数学的概念に明快さをもたらし、それらを統合する物語です。



では、証拠を自動的に生成するとどうなりますか？ ある興味深い例がありました。15年前に新しい科学に取り組んでいて、ブール代数の公理の最も単純なシステムで作業を終えたときに調べました（判明したように、それはたった1つの公理で構成されています（p◦q）◦r） ◦（p◦（（p◦r）◦p））== r）。 公理系の一貫性を証明するために、方程式論理（現在はFullSimplify関数に組み込まれています）に基づいた定理の自動証明システムを使用しました。 そして、生成された証拠を本に含めました。







343のステップが含まれており、標準のフォントサイズではおそらく40ページの印刷が必要です。 そして、私には思えるが、人にとっては完全に読めない。 誰かが証明を81個の補題に分割すると理解に役立つと考えるかもしれません。 しかし、どのように試しても、この自動証明を人が理解できるものに変えることはできませんでした。 そのような証拠が存在することは素晴らしいことですが、それだけでは声明を証明する以外には何も言いません。

物語としての証拠

ここでの問題は、証拠の要素に「認知の歴史」が含まれていないことだと思います。 証明のキーポイントとして補題のセットを選択したとしても、それらは認知的なつながりを持たず、歴史によって結び付けられません。 それらは、コンテンツやつながりのない単なる事実です。



このプロセスを改善するには？ 多数の類似証明を生成する場合、類似補題をより適切に区別できるため、より明確で意味のあるものになります。 確かに、証拠の全体像をすばやく確認するのに役立つ視覚化方法があります。 さらに、もちろん、数学文献で知られているすべての定理の基礎を管理し、自由に使用できる場合、生成された補題をこれらの定理に自動的に関連付けることができます。



現時点では、これがどの程度可能になるかはまだ明らかではありません。 実際、4色の定理、ケプラー仮説、または最も単純な普遍的なチューリングマシンなどのコンピューター証明の既存の例に基づいて、自動的に生成された補題は文学の定理とほとんど相関しないという印象を受けます。



しかし、これにもかかわらず、十分な労力で、Wolfram | Alpha Proの段階的なソリューションシステムであることを人々が理解するという証拠を生成できることを示す少なくとも1つの例を知っています。 1日数百万回、学生や他のユーザーは積分などの計算を行い、Wolfram | Alphaを使用して他の計算を行い、このシステムに段階的なソリューションを提供するよう依頼します。







積分を見つけることは、高品質の段階的なソリューションを示すよりもはるかに簡単であることに注意してください。 同時に、人にとって理解可能で自然なソリューション手順を見つけるには、かなり複雑なアルゴリズムとヒューリスティックが必要です。 しかし、Wolfram | Alphaの段階的な解決策の例は、適切な努力により、人が「物語」として読むことができる証拠を生成し、おそらくそれらを可能な限り単純かつ短くすることさえ可能になるという希望を与えます（「神の書からの証拠自体「ポール・エルドスが言うように）。



もちろん、このような自動メソッドは、最終的に、たとえば証明などのオブジェクトの要素の高品質なリンクに役立ちますが、数学の包括的なアイデアや動機を定義するためではなく、実際にほぼ接続することさえできません。 言うまでもなく、純粋な数学に関する現代の記事もこの機能を非常に不十分に実行していますか？ 厳密さと正確さを確保したいため、多くの記事は非常に正式に書かれています。 著者の深いアイデアと動機はそれらに表現されていません-その結果、数学のいくつかの重要なアイデアは口頭でのみ伝達されます。



間違いなく、純粋な数学のための一歩は、そのすべての内容を結合する機会になるでしょう。 この場合、純粋数学の正確なシンボリック言語は、現在どこにも記述されていないこれらの重要なポイントのいくつかの明示的な表記法の形成を簡素化します。一つのことは疑いなく明らかです。そのような言語のおかげで、例えばWolfram言語の通常のコードの形で、あらゆるソースから定理を見つけ、それをどこでも貼り付けて使用することができます。



しかし、自動化が純粋な数学で意味をなすかどうかという問題に戻ります。Wolfram | Alphaのように見える「純粋な数学のアシスタント」がいることは、人間の数学者にとって有用であることは絶対に明らかです。また、高品質で正確なシンボリック言語- 標準的な数学表記の続きであるMathematica Pura 言語-を使用すると、数学のすべての概念を定式化、確認、および組み合わせるのに非常に便利で便利であることもわかります。

自動開封

「自分自身に没頭し、自分で数学的計算を実行する」コンピューターはどうでしょうか？明らかに、コンピューターは一連の定理を定式化し、ヒューリスティックな方法を使用して、人間の数学者にとって興味深いと思われるものを強調することさえできます。数学文献のコレクション全体を所有している場合、広範な「経験的メタ数学」を構築することができます。これに基づいて、特定の特性を持つ定理を選び出します。 「予想外」または「強力」と見なすことができます。WolframTonesの Webサイトにあるように、これは特に複雑ではありません。、そのサイトで人々が選択するものを研究することによって得られた美的基準をコンピューターが適用します。



しかし、本当の疑問は、コンピューターが新しいアプローチと新しい構造、そして最後に新しい数学理論を作成できるかどうかということです。もちろん、列挙によって得られるいくつかの定理は非常に興味深いものであり、それらの受信は新しい知識の獲得を示します。この場合、もちろん、コンピューターが多数の定理（問題ではない-彼によって確立された、または文献で見つかった）を取得し、それらを結び付けるいくつかの新しい原則を定義する接続を発見し始めると、非常に興味深いでしょう。しかし、私が考えるように、時間の経過とともに、コンピューターは新しいデザインを検出できるだけでなく、それらに名前を付けて説明できるようになると期待できます。もちろん、コンピュータが何をすべきかを決定できるのは人だけですが、多くの点で彼らの活動は信じています、純粋な数学に携わる人々の仕事と見分けがつかなくなるでしょう。



このすべてはかなり遠い未来に残っていますが、今では数学的な事実を検出する優れた方法がありますが、これは実際には実験的な数学になりうる程度には使用されていません。この概念を理解する人は少し異なります。私の観点からは、これは数学システムの実験を行うことによる数学システムの研究です。たとえば、セルオートマトンの特定のクラス、非線形偏微分方程式、数値シーケンスなどについて学習したい場合は、考えられる特殊なケースのセットを準備して計算し、結果を観察します。



このようにあなたは多くのものを見つけることができます。そして、もちろん、このパスは、純粋な数学の従来の方法論を使用して調査できる観測と仮説を定式化するために非常に有益です。しかし、そのような経路の真の方向性と得られる結果は、純粋な数学者が数学で通常理解するものに適合しません。これは、「動植物」やすべての可能なシステムの世界の原理の研究に似ており、定理と証明を使用して調査および説明できる数学的構造の構築ではありません。それが、私の本のタイトル（新しい科学の種類）を引用する価値がある理由です-このプロセスは、既存の数学の一部にすぎないものではなく、新しい種類の科学と見なされるべきです。



実験数学と「科学の新形態」について言えば、驚くべきことは、純粋な数学がまったく機能するということです。誰かが数学システムについて完全にarbitrary意的な質問をし始めると、それらの多くが終わるからです。解決できないままになります。



これは、誰かがすべての可能なプログラムの計算された宇宙にいる場合に特に明らかですが、これは典型的な数学的システムを表すプログラムにも当てはまります。それでは、なぜ普通の純粋数学の分野のほとんどの問題がまだ不溶ではないのでしょうか？答えは、純粋な数学は暗黙のうちに学習対象を選択しようとするということですそれにより、不溶性の問題を回避します。ある意味では、これは歴史の結果であるように思われます：純粋数学は、開発に成功して得られたものに従い、最終的に不溶性の問題を回避し始め、現代の純粋数学の全体を形成する数百万の定理を生み出しました。



そのため、いくつかの問題と方向性を特定しました。しかし、計算された知識を純粋な数学に導入するという点で、私たちは実際どこにいるのでしょうか？

アイデアに命を吹き込む

関連する研究には長い歴史があります。これは何世紀も前のペアノ、ホワイトヘッド、ラッセルの仕事であり、ヒルベルトの問題です。セット理論とカテゴリー理論の開発。 1960年代、これらは証拠構造を表す最初のコンピューターシステム（Automathなど）でした。その後、1970年代に始まったMizarのようなシステムでは、証拠のコンピューター基盤を提供する試みが行われました。これらは現在、CoqやHOLなどのサポートシステムを成長させています。



これらすべての開発には1つの重要な特徴があります。それは、数学の「低レベル言語」の定義として考えられたものです。現在存在するほとんどのコンピューター言語と同様に、それらには限られた数の基本構造が含まれており、特定のユーザーまたは既製のライブラリーを使用して、ほとんどすべての必要な新しいオブジェクトを外部のどこかからロードすることを推奨しています。



しかし、Wolfram言語の新しい考え方は、可能な限り大量の関連知識が言語自体に慎重に埋め込まれている知識ベースの言語を持つことです。そして、汎用コンピューティングに関しては、最も効率的で広く適用可能な方法で計算を純粋な数学に導入するために、知識ベースの言語のアイデアが非常に重要になると思われます。



では、Mathematica Pura の作成には何を含める必要がありますか。これは、現代の構造と純粋な数学のオブジェクトを含むWolfram言語の拡張機能です。最低レベルでは、Wolfram言語は任意の文字式を操作します。それは絶対に何でも構いません。ただし、言語では、このような式を多くの特定の目的に使用します。たとえば、記号xは代数変数を示すために使用できます。このことを念頭に置いて、Wolfram言語には記号式を処理するための多くの機能があります-数学式または代数式として解釈されます-そしてそれらに対して様々な数学演算を実行します。Mathematicaで



実装された数学装置そしてWolfram言語では、今日では「実用的な」計算数学に重点が置かれています。現時点では、19世紀以前に存在していたほとんどすべての数学を網羅しています。しかし、より現代的な数学はどうでしょうか？歴史的に、数学自体は約100年前に変容を経験しました。芸術のさまざまな分野を捉えたアールヌーボースタイルのように、その独自の傾向は数学に現れました。外界とはまったく関係なく、完全に正式に登場する構造が考慮されました。



このような数学ブルバキの研究から始まり、その後、20世紀に純粋数学の主流になりました。必然的に、そのような数学の大部分は抽象的な構造の作成に費やされ、それはその後研究されます。最も単純なケースでは、これらの構造は何らかのタイプ階層を使用して表すことができるようです。しかし、これらの型は完全に記述される必要があり、すぐに全代数または型計算が形成されます-Wolfram言語のように、型の記述だけでなく、任意の頭部を持つ一般的なシンボリック式を使用できます。



この投稿で前述したように、現代の純粋な数学を表現するために必要な構造を実装するために、あらゆる種類の新しい組み込み関数と標準化されたデータオブジェクトを使用する予定です。もちろん、十分な機会があり、便利で理解しやすい純粋な数学で作業できるシステムを作成するには、長年の注意深い開発が必要になります。しかし、一般に、例えばリーマン面のモジュールによる微分可能性の概念または他の何かと作業することを可能にするシンボリックな構造を作成するのに根本的な困難はありません。これらはすべて、たとえば、3次元ラスターイメージの表現、リモートコンピューティングの実装、外部のキュレートされた構造化データベースへのアクセスなどの言語開発の問題です。



それで、すべての数学文献からの定理の監督について何が言えるでしょうか？Wolfram | AlphaおよびWolfram Languageを使用して、たとえばWolfram Functions SiteやWolfram Connected Device Projectを使用すると、さまざまなオブジェクトに関する構造化データの巨大なデータベースを作成し、最新の状態に保つプロセスですでに豊富な経験があります。この種のデータを計算可能にします。

例eCF-継続的な部分プロジェクト

しかし、数理定理の組織と順序が何であるかを明確にするために、過去2年間、Alfred Sloan Foundationが支援するWolfram Foundationに基づくパイロットプロジェクトを実施しました。 このプロジェクトでは、非常に具体的で十分に開発された数学の分野、すなわち連続分数の研究を選択しました。 鎖分数は古代から継続的に研究されてきましたが、1780年から1910年の間に人気のピークに達しました。 合計で、それらは約7,000冊の書籍と記事に記載されており、合計ボリュームは約150,000ページです。



約2,000のドキュメントを選択し、それらから定理やその他の数学的情報を抽出しました。 作業の結果は、約600の定理、1,500の基本式、10,000の微分式でした。 数式は計算された形式で直接提示されたため、Wolfram Functions Webサイトで300,000を超える数式に簡単に添付でき、それぞれがWofram | Alphaで実装されました。 しかし、最初は定理を最初の出版物の場所、定理の著者などの特定のプロパティを持つオブジェクトとして単純に考えました。さらに、この段階でも、Wolfram | Alphaにいくつかの注目すべき機能を挿入することができました。







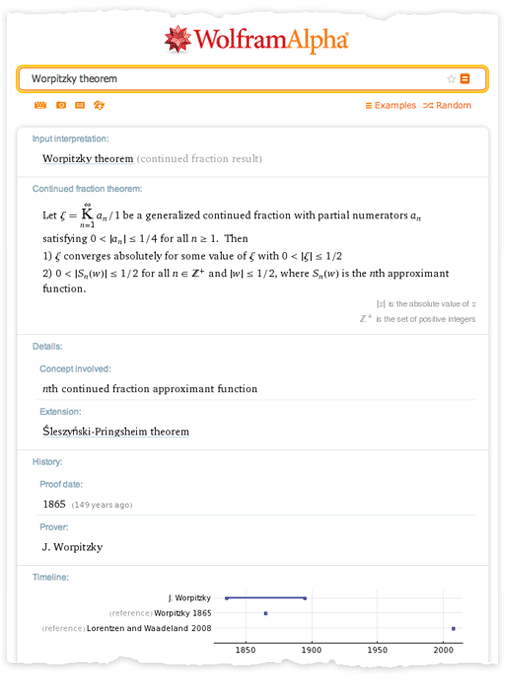
しかし、定理の内容を計算可能な形式に変換しようと試みました。 これには、LebesgueMeasure（ルベーグ測定）、ConvergenceSet（収束のセット）、LyapunovExponent（リアプノフ指数）などの新しい設計の導入が必要でした。 しかし、定理の正確な記号表現を作成する上で根本的な問題はありませんでした。 これらのアイデアのおかげで、Wolfram | Alphaで同様の計算を実行することが可能になりました。















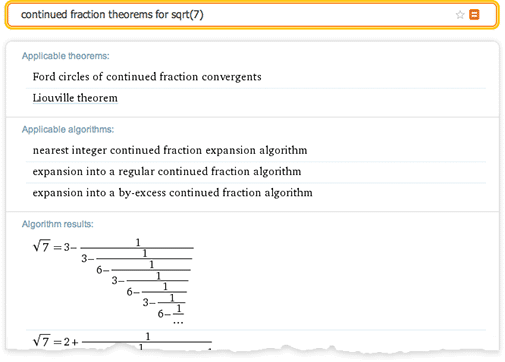
継続的な分数に関するプロジェクトの興味深い機能（要するに「eCF」）は、情報を整理するプロセスが実際に数学の新しい発見につながった方法でした。 ロジャースとラマヌジャンの継続的な断片に関する50以上の記事の研究が完了すると、考慮に入れない場合があることが明らかになりました。 したがって、計算結果は、ラマヌジャンが残したこの研究分野のギャップを埋めました 。







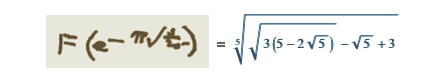
知識のキュレーションとゼロからの知識の作成の間には常にトレードオフがあります。 そのため、例えば、これはWolfram Functions Webサイトの場合であり、ディレクトリや他の文献で見つかった関数間の関係の中核が常に見つかっています。 しかし同時に、新しい関係を生成して計算する方が、検索で文献を調べるよりもはるかに効率的であることがわかりました。







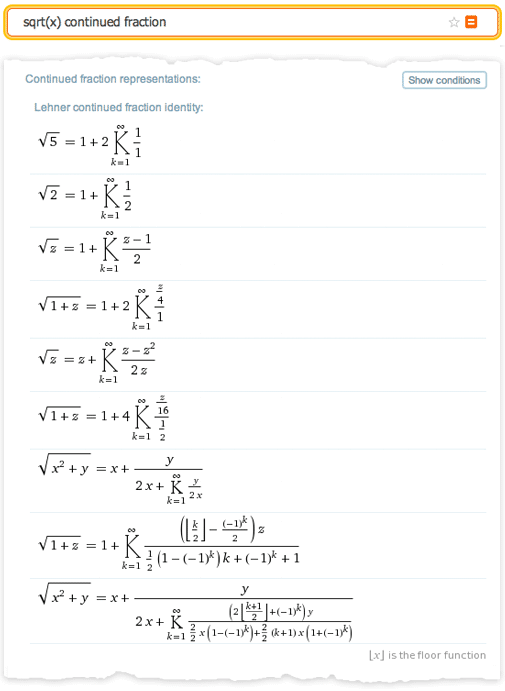
しかし、目的が正確に組織と知識の順序付けである場合、すべての数学文献の分析には何が必要ですか？ このプロジェクトの間、各定理を計算可能な形式に変換するには、数学者が約3時間作業する必要がありました。 しかし、この作業はすべて手動で行われ、大規模なプロジェクトでは、特にWolfram | Alphaの自然言語認識システムの拡張により、ほとんどの作業が自動的に行われると確信しています。



もちろん、作業の過程で、あらゆる種類の実際的な問題が発生します。 新しい記事は主にTeXで書かれているため、すべての数学表記で定理とそれらを区別することはそれほど難しくありません。 しかし、古い記事はスキャンする必要があり、これにはまだ開発されていない数学記号と数式の光学認識システムが必要です。



また、記事で定式化された定理が本当に正しいかどうかに関して、特定の困難があります。 そして、100年前に定理が有効であると認識されていたとしても、その定理が今でも有効であるかどうかはわかりません。 たとえば、連続分数の分野では、1950年代以前に定式化された多くの定理がありますが、一度証明されたものの、複雑な変数の多価関数の分岐点とカットラインを考慮していなかったため、最近は真とは見なされません。



この場合、結局、多くの優秀な数学者が組織と注文プロセスを導き、定理を計算可能な形式に変換するために必要です。 しかし、ある意味では、数学者のそのような動員は普通のものではありません。 数学ジャーナルZentralblattが1931年、またはMathematical Reviewsジャーナルの発行開始時に1941年に設立されたとき、このような科学者の連合が必要でした。 （おもしろい、両方のジャーナルの創始者兼編集長はオットー・ノイゲバウアーでした。彼は80年代初期に高等研究所で私から廊下を少し進んだところ、バビロニアの数学的な作品を解読することしかしていないと思っていましたこの投稿の調査を行うまで）。



システムで純粋な数学を記述するためのシステムを作成するということになると、興味深い例があります。Theoremaは1995年にBruno Buchbergerによって発表され、最近バージョン2に更新されました。TheoremaはWolfram言語で記述され、次のような環境を提供します数学的な定式化と証明を表示し、定理の自動証明などのための完全な計算アルゴリズムを実装します。







間違いなく、このシステムは最終的に作成されるものの要素になります。 しかし、一般に、プロジェクトは必然的に非常に大規模になることが判明します。これはおそらく、世界初の「大きな数学」（「大きな数学」）の例です。 このプロジェクトを完成させることは可能ですか？ 重要な要素は、言語を開発し、必要なインフラストラクチャを構築する技術的な能力を手に入れたことです。 しかし、これに加えて、この科学のすべての可能なセクションからの個々の数学者の参加がそうであるように、プロジェクトは世界の数学コミュニティに強い関心を必要とします。 さらに、現実には、これは明らかに商業的な基盤に置くことができるプロジェクトではないため、プロジェクトの開発に必要な約1億ドルを非営利的なソースから収集する必要があります。



しかし、これは、純粋な数学の鍵となることを約束する真剣かつ重要なプロジェクトです。 主要な発見がなされたとき、各地域には独自の「黄金時代」があります。 そして、ほとんどの場合、そのような「黄金時代」の始まりは、新しい方法論の作成または新しいテクノロジーの出現でした。 そして、これは、純粋な数学の分野で起こると確信しています。 数学的知識の整理と整理に努力を向け、それらを使用し、それらに基づいて計算された形式の知識を作成するシステムを構築することができれば、純粋な数学の広大な遺産を保存し広めるだけでなく、この急速な成長に弾みをつけることができます科学のセクション。



このような大規模なプロジェクトには、信頼できるガイダンスが必要です。 そして、私は常に作業の一部を行い、その実装に必要な基本技術を取り入れる準備ができています。 現在、プロジェクトのさらなる発展のために、全世界の数学コミュニティの関心が必要です。 20世紀の20年を、数千年の純粋数学の歴史の中で本当に重要な時期にする機会があります。 やってみましょう！