自然数での操作は、値と特性の両方で直接可能です-数値のプロパティ。 このような操作の利便性は、主に数値のモデルによって決まります。 モデルの種類が限られており、構造が単純であることが望ましい。 自然数のモデルの特性の説明(ちなみに、およびその他の数値)は、定式化された形式で、定量的に持つことが望ましいです。 プロパティインジケータの値の数値のビット深度への依存性を排除するか、そのような依存性のないプロパティを選択する必要があります。 分類には基本的にプロパティがあります-これは形式化の要素です。 作業の主な問題は数値の因数分解です。これに関連して、自然数の因数分解の定理のバージョンを以下で定式化します。
定理は、因数分解の難しさはすべての数について発生するわけではないことを示しています。したがって、複雑な因数分解手順をNRFのすべての数ではなく、それらの一部(より小さい)部分のみに適用する必要があります 定理のテキストは、この小さな部分を形式化し、さらに処理するのに便利にする方法を述べていません。 しかし、議論は、処理に便利なこのような小さなセットの数の表現の形成に焦点を当てます。
自然数の因数分解係数
いくつかの基本変換を連続して実行することによる任意の合成自然数Nは、次の形式の積で表すことができます。
N = 2 t 2 ∙3 t 3 ∙5 t 5 ∙(p k + 30∙t)、ここで0≤t i 、i = 2,3,5、tは正の整数、p k > 5は素数です。
定理
1. Nが合成偶数の自然数である場合、N = 2 t 2 ∙n 2の形式で表すことができます。
ここで、n 2≡1(mod 2)は奇数の合成数、t 2 = 1(1)...、および2∤n 2です。
2. N = n 2が数字5で終わる合成奇数の場合、N = 5 t 5 ∙n 5として表すことができます。ここで、n 5は合成奇数、t 5 = 1(1)...; および5∤n 5 ;
3. N = n 5が5で終わらない複合奇数であり、その畳み込み s(N) (桁の合計)が3の倍数である場合、N = 3 t 3 ∙n 3として表すことができます。ここでn 3-合成奇数
t 3 = 1(1)...; および3∤n 3 ;
4. N = n 3が最後の桁( 屈曲 )ϵ {1、3、7、9}の複合奇数である場合、N =(p k + 30∙t)の形式を持ち、t = 1( 1)...は自然数であり、p k ϵ {7,11,13,17,19,23,29,31}であり、たとえば、限界輪郭の概念と奇数のf不変量または既存の1つを使用して、因数分解を実行できます。既知の方法。
証拠の代わりに。 さらに、表3を含む作品のテキストは、本質的に定理の最初の部分の証明です(モデルの形で数を表すN = 30∙t + p k )。 プレゼンテーションの過程で、LFDの完全なモデルと切り捨てられたモデルが、フラットで3次元で表示されます。 すべての自然数のセットは、2つのサブセットに分割されます。 最初のものは、基本的な手段で因数分解された自然数を含んでいるため、直感的に知覚されます(素数2、3、5への可分性の最も単純な記号が使用されます)。 2番目のサブセットは、奇数の素数(3と5を除く)をすべて含む最小のサブセットであり、その分解は、特に大きな数の場合、現在の克服できない問題です。 最後に公開された因数分解された数値は、232桁の10進数で記述されています。
30k、30k±1、30k±3、...、30k±15のリストの形式でのNRFのよく知られた分析モデル
関係のk = 1(1)∞は、示されたサブセットのそれぞれに含まれるべき数のそれらをどのように記述することができるかを理解することを可能にします。すなわち、本質的にLDPのそのようなパーティションを実行します。
30の乗法表現の形式は30 = 2∙3∙5です。 30のモジュロ除数ゼロに匹敵する自然数N、
そのようなプロパティに違反する自然数のセットは、他の単純で明確に区別可能な属性を持つ等価クラスに分割されることがわかります。 したがって、作業のタスクは、NRFを2つのサブセットに分割し、さらに小さい番号の説明を、数字をさらに処理するためのシンプルで便利な形式で取得することです。
自然数のクラス。 分類の基礎として、数字の性質(s、f)の非常に簡単に定義された2つの指標を検討しています。 最初のメトリックはsで示されます
1≤s≤9は、数値の畳み込みと呼ばれ(これは数値の桁数の合計で、1桁に減じられます)、数値の3の可分性の特性を表し、2番目のインジケーターは記号fで示されます。
0≤≤9-数字の屈折 (末尾、最後の桁)と呼ばれ、有限の数字のプロパティが最後の桁を持つように特徴付けます。
例1 N = 4757、s(N)=((4 + 7 + 5 + 7 = 23)→(2 + 3))= 5; φ(N)≡N(mod10)= 7。
指数(s、f)によって特徴付けられる数値のペアのプロパティは、LDPを、指数のペアに対して同じ値を持つ非交差クラス(等価)に分割します。 数N = 4757が属する数のクラスの特性は、値(s、φ)=(5、7)とのペアです。
そのような特性によって識別可能な数のクラスの数T(s、f)は、数の2つの特性の各指標の値の変化の範囲の積によって決定されます。
T(S、)= S×= 9×10 = 90。
各クラスのボリュームには、無数の自然数が含まれていますが、その中にはクラス内で最小の数があります。 すべてのクラスの最小の代表を表1の左側に配置し、右側に(左のサンプルに従って)行の表のセルに次の自然数を入力し続けます。
表1-周期90の数値のクラスT(s、f)。NRFのフラットモデル
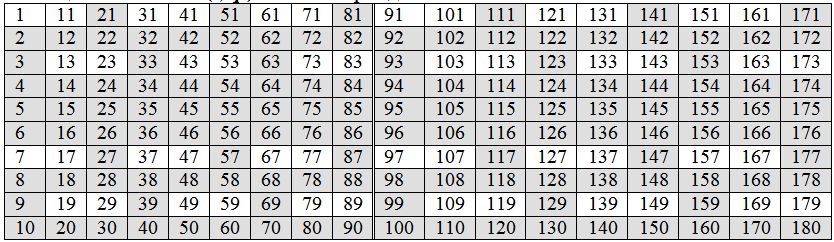
テーブルの内容(T-90番号のセット)を分析すると、10×9テーブルの左側で、すべての番号がクラス内で最小であり、異なる特性値(s、f)を持っていることがわかります。 10×9テーブルの右側は、左側と同様に、同じ特性(s、f)を持つ異なるクラスの代表で満たされていますが、要素の次の値(期間)は90単位増加しています。 このようなテーブルは無期限に継続でき、1番目(左)のテーブルにオーバーレイを使用して左にシフトできます。 その結果、3次元の平行六面体が得られます。この場合、ペア(s、φ)の固定値を持つ自然数のクラスを形成するすべての数値が、下のテーブルの各セルに書き込まれます。
3Dモデル
本質的に、NRFのさらに別の体積モデルを取得しました。 その利点は、重要な位置(例えば、素数を含む位置)を失うことなくNRFを大幅に削減できることです。 これを行う方法を示します。
最初に、5で終わる偶数と奇数を含む表1の行を消し、次に、3の倍数である数のクラスを削除します。 このようなクラスのテーブルセルは、テーブルの横の対角線に平行な対角線に属します。 表1では、削除されたセル(クラス)が塗りつぶしで強調表示されています。
塗りつぶされていないセルクラスT(s、f)は保持され、その数は24です(番号を削除した後の残りはセットT-24と呼ばれます)。これらは塗りつぶしなしのテーブルのセルに対応します。 残りのクラスで可能な屈曲は、φ= 1,3,7,9のみであり、各屈曲6畳み込み値、つまり24クラスです。 プライムがこれらのクラス内でのみ表示されることは明らかです。 実際、すべてのクラスの24の最小代表の左の表では、22が素数です。 残りの最小の素数7にそれ自体と次の素数11を掛けることで得られる2つのセル(24個のうち)だけが化合物番号7×7 = 49と
クラスの剰余ジェネレーターの代数群
NRFの改革を続け、30 = 2∙3∙5の数に戻ります。 8つの素数p(i)= {7,11,13,17,19,23,29,31}は、これを法とする8次剰余の乗法群E(オイラー群)を形成することを思い出してください。 単位要素は素数31、p(i)≡31(mod30)= 1で識別されます。ラグランジュ定理(グループの順序)により、グループは2次および4次の適切なサブグループを持つことができます。 8次グループ(11、19、および29)の要素は2次です。 (7,13、17、23)4次と単位。 4次の3つのサブグループがあります:1つ(1,11,19,29)-インボリューションのみを含み、2つのサブグループは周期的です:
7×7≡49(mod30)= 19; 19×7≡133(mod30)= 13; 13×7≡91(mod30)= 1;
11×19≡209(mod30)= 29; 11×29≡319(mod30)= 19; 19×29≡551(mod30)= 1;
17×17≡289(mod30)= 19; 19×17≡323(mod30)= 23; 23×17≡391(mod30)= 1;
驚いたことに、24クラスのすべての数字| T(S、Φ)| = 3×8は、集合p(i)の各代表によって生成された8つのクラスのみで構成されるクラスのファミリーに変換されます。 数字の新しいクラスでは、要素は90の周期ではなく、3倍小さい30の周期で続きます。
表2-mod30による残基グループ(p k )の乗法サブグループ
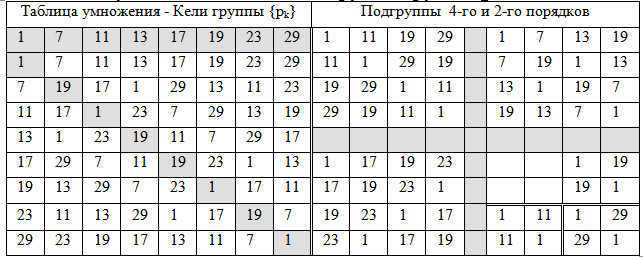
クラスは、3つのペア(2,1)、(5,1)、(8,1)の数の変曲と畳み込みを考慮して形成されます。 (4.1)、(7.1)、(1.1); (2.3)、(5.3)、(8.3); (4.3)、(7.3)、(1.3); (7.7)、(1.7)、(4.7); (8.7)、(2.7)、(5.7); (7.9)、(1.9)、(4.9);(8.9)、(2.9)、(5.9);
以下の表3に、これらの8つのクラスの初期フラグメントを示します。 3または5の倍数ではない奇数のN> 31は、N = p(i)+ 30tの形式であり、表3に示す8つのクラスのいずれかに分類されます。
表3-周期が30の数字のクラス。素数{p k }は塗りつぶしで強調表示されます

表の表面的な分析でさえ、単純さ、複雑さ、および数の因数分解の可能性に関するいくつかの結論を引き出すことができます。
-すべてのクラスジェネレーターのすべての度合い、つまり 素数は複合的です。
-このジェネレーターの列セル内のジェネレーターの倍数を持つ行には、除数がジェネレーターである合成数が含まれます。
-ウラムスパイラルの素数の禁止領域に属する番号-化合物、最初の千のそのような数の例:143,161,203,217,323,451、517,539,473、611,637など
-217 = 210 + 7 = 7(30 +1)= 7×31のように、共通因子の和差とブラケット外に分解できる数値。 1397 = 1270 +127 = 127(10 +1)= 127×11。
したがって、基本的な手段と操作により、T-8の奇数のNRFのセットを選択することができます。これは、理論的問題と実用的問題の両方を解決するためのさらなる研究の対象として機能します。 暗号学と情報セキュリティの分野におけるこのような問題には、HFBCH、数の単純さを確立する問題、有限体の離散対数の問題、楕円曲線の点群が含まれます。
T-8番号のセットは特別な方法で構成され(8つのクラスで構成)、クラスの最小の代表は30を法とする残基のグループを形成します(φ(30)= 8)。 このプロパティは、列番号が既知の数値のペアの積の結果の列番号を決定します。 Keliグループテーブルは、この問題の解決策を提供します。
例の目的は、セットのT-8に含まれる数値、行番号、および列番号の値の間の関係に関する情報を示すことです。
表3を使用してセットT-8の数を因数分解する可能な方法の1つ。
例2 奇数の正の整数(snc)を与えます
N =1727。因数分解する必要があります。 セットT-8でこの番号の位置を見つけます。行番号N / 30 = 57(小数部の整数部分が取られます)、列番号(名前)N-30∙57 =17。この同じ列で製品7∙11 = 77、番号を指定しますその行は2です。
各仕切りを保存しようとしています。 d1 = 7を維持し、別の約数Nは次の形式を取ります。
d2 = 11 + 30∙t、ここでtは行番号と格納されている除数の差によって決定されます
t =(57-2)/ 7 = 7.85。 7が特定の数の約数ではないことを示す小数値を取得しました。実際、diが特定の数の約数であるかどうかは試用除算によってすぐにわかります。
d2 = 11を保存します。別の除数はd1 = 7 + 30∙tの形式を取ります。ここで、tは行番号と格納された除数t =(57-2)/ 11 = 5の差によって決まります。
実際、1727/157 = 11。
例3:奇数の正の整数(snc)を指定します
N = 4294967297、テーブル外。 分解するために必要です。 前と同様に、T-8のセットでこの番号の位置を見つけます。
行番号N / 30 = 143165576、
列番号N-30∙143165576 = 17。
同じ列で、製品7∙641 = 4487を指定します。その行番号は149です。
各仕切りを保存しようとしています。 d1 = 641を保存し、別のディバイダーは次の形式を取ります。
7 + 30∙t、ここでtは行の差と格納されている除数によって決定されます
t =(143165576-149)/ 641 = 143165427/641 = 223347
値t = 223347は整数であるため、641は元の数Nの約数です。
実際、N / d1 = 4294967297:641 = 6700417は素数(別の約数)です。