はじめに
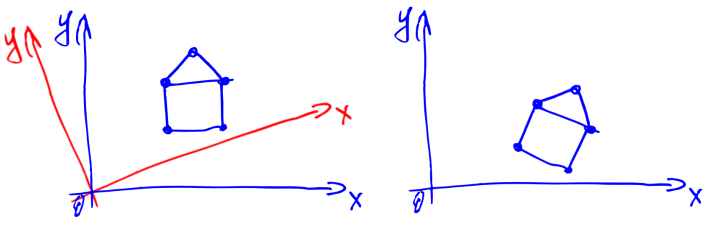
チャレンジ。 次のような2次元の画像があると仮定します(家)。
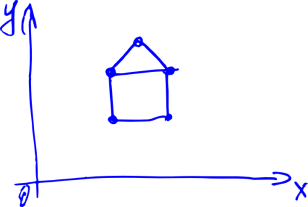
また、原点から家をOXの方向に見たとします。 これで特定の角度を反時計回りに回しました。 質問:家は私たちにとってどのように見えますか? 直観的には、結果は下の図とほぼ同じになります。
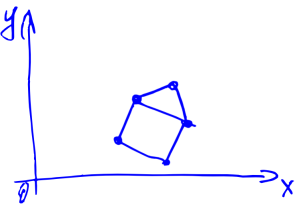
しかし、結果を計算する方法は? そして、何より最悪なのは、3次元空間でそれを行う方法ですか? たとえば、カメラを非常に巧妙に回転させた場合:最初にOZ軸に沿って、次にOX、次にOYに沿って?
これらの質問に対する回答は、以下の記事に記載されています。 まず、家を数字の形で表す方法(つまり、ベクトルについて説明します)、次にベクトル間の角度(スカラー積)について、そして最後に、カメラの回転方法(回転行列について)について説明します。
ベクトル座標
ベクトルについて考えてみましょう。 つまり、長さと方向のある矢印についてです。
コンピュータグラフィックスに適用されます。このような矢印はそれぞれ、空間内のポイントを定義します。
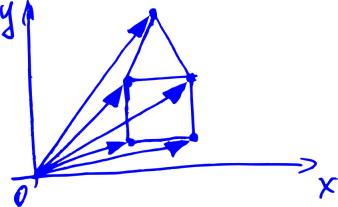
また、それらを回転させることを学びたいです。 上の写真のすべての矢印を回すと、家が回るからです。 これらの矢印を使用してできることは、数字を加算して乗算することだけだと想像しましょう。 学校のように:2つのベクトルを追加するには、最初のベクトルの最初から2番目のベクトルの終わりまで線を引く必要があります。
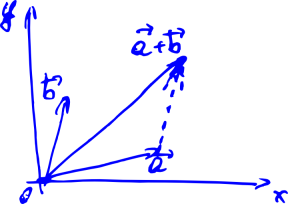
ここでは、2次元ベクトルに焦点を当てます。 そもそも、これらのベクトルを数字で書く方法を学びたいと思います。なぜなら、それらを紙に矢印の形で描くたびに、あまり便利ではないからです。
これを行う方法を学習します。どのベクトルもいくつかの特別なベクトル(OXとOY)の合計として表現でき、特定の係数を掛けることができることを思い出してください。 これらの特別なベクトルは基本と呼ばれ、係数はベクトルの座標に他なりません。 基底ベクトルを
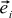 (ここでiはベクトルのインデックスで、1または2のいずれかです)、考慮されるベクトルは
(ここでiはベクトルのインデックスで、1または2のいずれかです)、考慮されるベクトルは 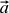 、および後者の座標
、および後者の座標 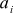 次に、式を取得します
次に、式を取得します
(1)
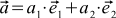
これらの座標は、この基準に対して一意であることを示すことができます。
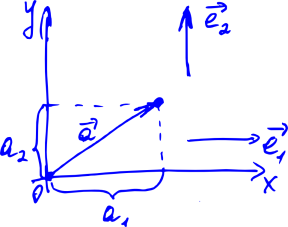
矢印に座標を割り当てることの利点は明らかです。以前は、ベクトルを記述するために常に矢印を描画する必要がありましたが、今は2つの数値を書くだけでこのベクトルの座標を作成できます。 たとえば、次のように書くことに同意できます。
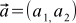 。 または:
。 または: 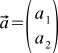 。 それから
。 それから 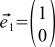 、そして
、そして  。 いいね
。 いいね
実際の数学では、手順は多少異なります。 まず、オブジェクトが満たす必要のあるプロパティを記述し、それらをベクトルと呼びます。 彼らは非常に自然です。 たとえば、ベクトルは加算(2つのベクトル)と数値演算による乗算をサポートする必要があります。 2つのベクトルの合計は、項の順序に依存してはなりません。 3つのベクトルの合計は、ペアで追加する順序に依存しません。 完全なリストはWikipediaにあります。
いずれかの種類のピースがこれらのプロパティを満たしている場合、これらのピースはベクトルと呼ばれます(これはアヒルのタイピングです)。 そして、これらの断片のセット全体がベクトルまたは線形空間です。 上記の特性は公理と呼ばれ、ベクトル(または線形空間—「 線形代数 」という名前が由来する)の他のすべての特性はそれらから導出されます。 例えば、ベクトルの中には、ベクトルが式(1)で表現できる特別な基底ベクトルが存在し、座標へのこの展開はこの基底に対して一意であると推定できます。 私たちの矢がこれらの公理を満たしていることをすぐに示すことができます。 公理を満たす他のオブジェクトに出会った場合、理論のすべての結果をすぐに適用できるため、公理的アプローチは便利です。 さらに、この方法では、理論の初めに指の矢印の定義を避けます。
(公理から)ベクトルを追加すると、対応する座標が追加され、ベクトルに数値を乗算すると、すべての座標に同じ数値が乗算されることが簡単に示されます。 次の図のように2つのベクトルを追加するために、それらを描画することはできません(最初のベクトルの最初から2番目のベクトルの終わりまで線を描画しません)が、たとえば、
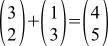 。
。

スカラー積
ここで、2つの任意のベクトルaとbの特別な関数を紹介します。これをスカラー積と呼びます。 次のように示します。
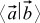 。 これらの流行のかっこは、科学的にブラとケトのベクトルと呼ばれます。 それらからの利点はまだありませんが、見た目は素晴らしいです-さらに、この表記法は、特に数学的な詳細や量子力学を扱う場合には、まだ深い意味があります。
。 これらの流行のかっこは、科学的にブラとケトのベクトルと呼ばれます。 それらからの利点はまだありませんが、見た目は素晴らしいです-さらに、この表記法は、特に数学的な詳細や量子力学を扱う場合には、まだ深い意味があります。
公理的アプローチの精神では、スカラー積がいくつかの公理を満たすことのみが必要です。 最初のベクトルの代わりに、型のベクトルの合計を取る場合
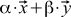 、それから私たちは欲しい
、それから私たちは欲しい 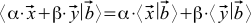 。 ここで、ギリシャ文字は因子であり、xとyはベクトルです。 また、2番目のベクトルの代わりにそのような合計を代入すると、同じ変換を行うことができます(ベクトルの合計のスカラー積もスカラー積の合計になり、係数も角かっこから取り出されます)。 さらに、値が必要です
。 ここで、ギリシャ文字は因子であり、xとyはベクトルです。 また、2番目のベクトルの代わりにそのような合計を代入すると、同じ変換を行うことができます(ベクトルの合計のスカラー積もスカラー積の合計になり、係数も角かっこから取り出されます)。 さらに、値が必要です 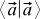 常に非負でした。 最後に、欲しい
常に非負でした。 最後に、欲しい 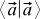 ベクトル自体が
ベクトル自体が 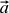 ゼロ。 そうそう、もっと
ゼロ。 そうそう、もっと 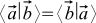 。
。
紙の矢印に定規と分度器を追加すると、学校で知られている機能がこれらの公理を満たします。
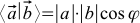 ベクトルの長さが定規によって測定される場合、ベクトル間の角度
ベクトルの長さが定規によって測定される場合、ベクトル間の角度 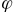 -分度器。
-分度器。
定規と分度器がない場合、スカラー積からベクトルの長さを決定できます—
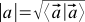 -そして、ベクトル間の角度
-そして、ベクトル間の角度 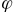 :
: 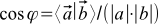 。 もちろん、角度はスカラー積の決定方法に依存します。
。 もちろん、角度はスカラー積の決定方法に依存します。
ベクトルの個々の座標を通してスカラー積がどのように表現されるかを見てみましょう。 次のような2つのベクトルaとbがあるとします。
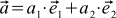 、
、 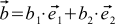 。 それから
。 それから 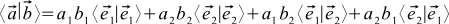 。
。
よく見えません 生活をより良くするために、私たちは特別な座標系でのみ働き続けます。 基底ベクトルが単位長さを持ち、互いに垂直である座標系のみを選択します。 言い換えれば
(2a)
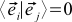 もし
もし 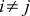
(2b)
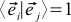 もし
もし 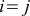
このようなベクトルは正規直交と呼ばれます。 正規直交座標系のスカラー積の式は、認識を超えて変換されます。
(3)
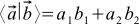
この記事のすべての座標系は正規直交であると想定されています。 驚くべきことに、式(3)の結果は、選択する座標の正規直交基底に依存しないという構造になります。
「ベクトルの座標への分解」(この段落の後で再び説明します)を注意深く見ると、ベクトルの座標は、対応するベースベクトルへの投影にすぎないことが疑われます。 つまり、元のベクトルといずれかの基底ベクトルのスカラー積の値:
(4)
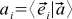

確かに、例えば、
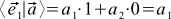 。 これはトートロジーのようです。なぜなら、それ自体の基底の基底ベクトルの座標は常に(1、0)と(0、1)になるからです。 ただし、他の基底ベクトルを使用して、古い基底で表現することもできます。 たとえば、新しい正規直交基底は古い基底で次のように見える場合があります
。 これはトートロジーのようです。なぜなら、それ自体の基底の基底ベクトルの座標は常に(1、0)と(0、1)になるからです。 ただし、他の基底ベクトルを使用して、古い基底で表現することもできます。 たとえば、新しい正規直交基底は古い基底で次のように見える場合があります 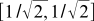 そして
そして 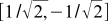 。 そして、例えば、ベクトルの最初の座標を決定できます
。 そして、例えば、ベクトルの最初の座標を決定できます 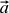 式(4)による新しい基礎
式(4)による新しい基礎 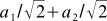 。
。
「ただし、式(3)はスカラー積の定義として使用でき、基底ベクトルの正規直交化は必要ありません。」 そして、式(3)がスカラー積の定義の1つとして機能することは正しいでしょう。 ただし、微妙な点があります。座標系が変更された場合、同じ式が別の基底からのベクトルaとbの座標で同じ数になることを示す必要があります。 そして、これはすべてのベースが正規直交である場合にのみです。 これは、次のセクションを読むと表示できます。
座標系の回転
座標系全体を変更した場合、ベクトルの座標がどのように変化するかを調べてみましょう。 座標系を変更する必要があるのはなぜですか? 少し考えてみると、座標系の回転が3Dまたは2Dモデリングのカメラの回転と同等であることが明らかになります(下の家を含むわずかに変更された画像を参照)。 そのため、座標系を回転させる方法を学ぶことがまさに必要です。
新しい座標系のベクトルaのi番目の座標を次のように示しましょう。
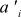 、および新しい基底ベクトル
、および新しい基底ベクトル 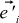 。 さらに、NEW基底のOLD基底ベクトルiの j番目の座標を次のように示します。
。 さらに、NEW基底のOLD基底ベクトルiの j番目の座標を次のように示します。 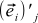 。 最後に、OLD基底のNEW基底ベクトルjのi番目の座標を
。 最後に、OLD基底のNEW基底ベクトルjのi番目の座標を  。 これで、元のベクトルと古い基底ベクトルを新しい基底ベクトルで表現できます。 すなわち
。 これで、元のベクトルと古い基底ベクトルを新しい基底ベクトルで表現できます。 すなわち
(5)
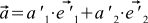 そして
そして
(6)
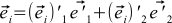
さらに、新しい基底ベクトルは、古い基底ベクトルに関して表現できます。
(7)
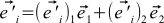
これらの拡張の一部を以下の画像に示します。
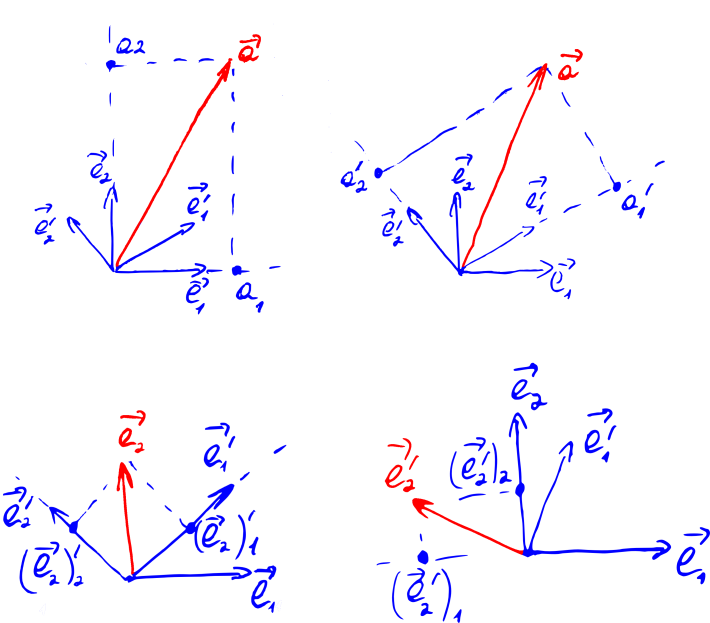
ここで、新しい基底のベクトルを通じて式(1)を書き換えます。
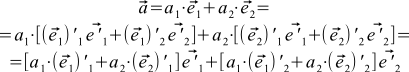
これを式(5)と比較し、ベクトルの座標が一意に決定されることを思い出すと、
(8)
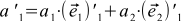 そして
そして 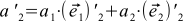
これらの式が方程式のように見えることは驚くべきことです(3)! それらはベクトルのスカラー積のように見えます
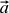 特定のベクトルで(これは偶然ではないことを以下に示します)。
特定のベクトルで(これは偶然ではないことを以下に示します)。
1つの式で方程式(9)を書くと、
(9)
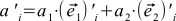
この式は、(4)、(1)、および(7)を組み合わせることにより、異なる方法で導出できます。
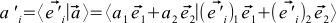 。 スカラー積のプロパティを思い出すと、この式は4つの合計に分割されます。 ここで、基底ベクトルが正規直交であることを思い出せば、
。 スカラー積のプロパティを思い出すと、この式は4つの合計に分割されます。 ここで、基底ベクトルが正規直交であることを思い出せば、 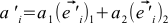 。
。
この式は式(9)とまったく同じではありません:代わりに
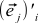 ここに立っています
ここに立っています 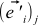 。 これは間違いではありません—ただ
。 これは間違いではありません—ただ 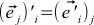 。 つまり、NEW基底のOLD基底ベクトルiのj番目の座標
。 つまり、NEW基底のOLD基底ベクトルiのj番目の座標 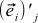 OLD基底のNEW基底ベクトルjのi番目の座標に常に等しい
OLD基底のNEW基底ベクトルjのi番目の座標に常に等しい 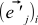 。 これは、式(4)でこれらの座標を表現しようとすると明らかになります。
。 これは、式(4)でこれらの座標を表現しようとすると明らかになります。
(10)
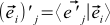 、
、 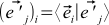
また、スカラー積は、ベクトルの積の順序に依存しません。
これらのスカラー積が異なる(単位)基底ベクトル間の角度であることを思い出すと、これはさらに明白になります。 もちろん、これらの角度は、時計回りまたは反時計回りに設定するかどうかには関係ありません。
回転行列
マトリックスに精通している場合は、式(9)(2つの式)をマトリックス形式で書き直すことができます。
(11)
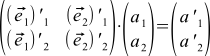
これはどういう意味ですか?! いつものように、ここには魔法はありません。左の数字と右のベクトルのこのプレートの乗算が式(9)として計算されることに同意します。 つまり、ラベルの各行に右側の列を乗算し(2つのベクトルのスカラー積を行うように)、結果を互いに下に書き込み、列も取得します。
ちなみに、このルールを2つのラベルの乗算に拡張できます。最初のラベルの各行に2番目の列を乗算し、結果をラベルに書き込むことに同意します。最初の行と最初の行と3番目の列の3番目の列の乗算を書き込みます。 式(11)は、このルールの特殊なケースになります。 概略的に、これはすべて下の図に示されています。
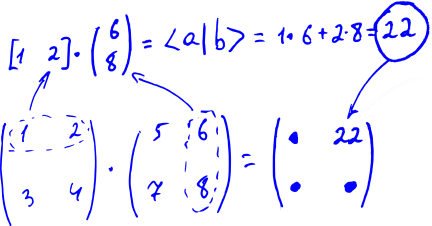
このベクトルと他のタブレットとの乗算の規則を備えた数字のタブレットは、マトリックスと呼ばれます。
行列乗算の規則は、スカラー積が、それを示すことに同意したことがわかった場合、さらに自然に見えます。
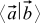 、実際には、ベクトルaが文字列であり、ベクトルbが列であると想定しています。 その前に、列にベクトルを書き込むことに同意しました。行ベクトルaは、実際には単なる逆ベクトルaではなく、特別な双対ベクトル空間のオブジェクトです。 しかし、正規直交基底の場合、元のベクトルと双対ベクトルの座標は一致するため(つまり、a行とa列は同じです)、これらの詳細はプレゼンテーションに影響しません。 すべて順調です。 また、一方で、スカラー積の式(3)は、行列乗算の特殊なケースです。
、実際には、ベクトルaが文字列であり、ベクトルbが列であると想定しています。 その前に、列にベクトルを書き込むことに同意しました。行ベクトルaは、実際には単なる逆ベクトルaではなく、特別な双対ベクトル空間のオブジェクトです。 しかし、正規直交基底の場合、元のベクトルと双対ベクトルの座標は一致するため(つまり、a行とa列は同じです)、これらの詳細はプレゼンテーションに影響しません。 すべて順調です。 また、一方で、スカラー積の式(3)は、行列乗算の特殊なケースです。
一般に、行列による乗算はベクトルの特定の変換に対応することが示されます。 「変換」の代わりに、 演算子と言うのが習慣です。 そして、行列乗算は線形演算子です。 さらに、線形演算子の場合、演算子行列は1つだけです。 ウィキペディアでそれについて知ることができます 。 ここで説明すると、記事は終わりません。
したがって、わかったように、座標系の回転は、3Dまたは2Dモデリングのカメラの回転に相当します。 したがって、式(11)の行列は回転行列と呼ばれます。 式(11)は、座標系の置換としてではなく、回転演算子の説明として解釈できます。
この行列の計算方法はまだ明確ではありません。 式(10)に戻り、単位ベクトル間の角度の余弦がスカラー積に等しいことを思い出せば、これは難しくありません。 次に、例えば、
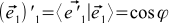 どこで
どこで 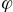 -座標系(カメラ)の回転角度。 定義によれば、回転が反時計回りの場合は正であり、時計回りに回転する場合は負です(下の図を参照してください-すでに関連していましたが、今では再び関連しています)。 ジオメトリまたは三角法を少しいじると、回転行列全体が次のようになることがわかります。
-座標系(カメラ)の回転角度。 定義によれば、回転が反時計回りの場合は正であり、時計回りに回転する場合は負です(下の図を参照してください-すでに関連していましたが、今では再び関連しています)。 ジオメトリまたは三角法を少しいじると、回転行列全体が次のようになることがわかります。
(12a)
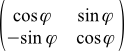
Wikipediaを見ると、そこの式は少し異なります:
(12b)
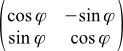
これがすべてです
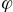 その中には、ベクトル自体(または家などのオブジェクト)の回転角があります。 回転が反時計回りに発生する場合も正と見なされます。 しかし、カメラの回転はオブジェクトの回転と反対です。つまり、カメラの回転角度はオブジェクトの回転角度と同じですが、反対の符号で撮影されます。
その中には、ベクトル自体(または家などのオブジェクト)の回転角があります。 回転が反時計回りに発生する場合も正と見なされます。 しかし、カメラの回転はオブジェクトの回転と反対です。つまり、カメラの回転角度はオブジェクトの回転角度と同じですが、反対の符号で撮影されます。
再び現在の図面:

素敵なささいなこと
これらの行列は非常に便利です。 さらに、2つだけでなく、3つと4つも乗算および追加できます。 行列は大文字で表記できます。 たとえば、 Tは回転行列の通常の指定です(システムまたはカメラの回転方法に依存します)。 次に、式(11)
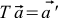 。
。
行列には単位行列があります。つまり、左側のベクトルで乗算されたベクトルは、それ自体のままです。 マトリックスも。 単位行列はテーブルのように見え、すべてゼロで埋められ、対角線上のみが単位です。 このような行列は、ゼロ度の回転に対応します。 それが回転不足です。 次のようになります。
(13)
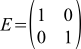
少し数えるか考えると、回転行列の乗算は次々に行われる数回の回転に対応します(ただし、右から左に異なる順序で)。 したがって、プログラムに以前に既知のターンが連続していくつかある場合は、急いでそれらを3次元世界のすべてのポイントに適用しないでください。 行列をより良く乗算し、共通の回転行列を取得して、すでに適用しています。
多くの行列の場合、最初の行列に2番目の行列を掛けると、単位行列が得られることがわかります。 これらの新しい行列は逆行列と呼ばれ、 Tについては
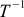 。 それは
。 それは 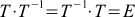 。
。
もう少し考えれば、そのような行列
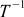 Tの反対のターンに対応する必要があります-Tを中和するターン これはすでに非常に便利です。 逆行列の計算方法を学べば、必要に応じてカメラを簡単に逆回転させることができます。
Tの反対のターンに対応する必要があります-Tを中和するターン これはすでに非常に便利です。 逆行列の計算方法を学べば、必要に応じてカメラを簡単に逆回転させることができます。
少し考えて、少しでもカウントすると、回転行列については、 特殊な構造 (式(10)を参照)があるため、逆行列を取得するのは非常に簡単です:左上から対角線に沿って行列を回転させるだけです右下隅(単位行列が単位行列に沿っている同じ対角線の)。 この操作は転置と呼ばれます。 一般的な場合の逆行列の検索よりもはるかに(はるかに)速いです。
三次元空間
最後に、3次元空間に進みます。 すべての数式は簡単に変換されます-ベクトルでは3つの座標、スカラー積では-3つの合計など。
複雑さは回転行列でのみ発生します。 回転は3回転(OX、OY、OZに沿って)のシーケンスとして表現できることはほとんど直感的に明らかです(ただし、表示するには少し作業する必要があります)。したがって、これら3つの回転角度で任意の回転を設定できます。 これらの回転に対応する3つの行列を乗算して、3次元の回転に共通の行列を取得できます(3つのパラメータ-座標軸に対する回転角度)。 彼女の外観はウィキペディアで見つけることができます。
3つの角度の代わりに、3次元の回転は、回転が行われる周囲のベクトルと、このベクトルに沿ってカメラを回転させる角度によって定義できることがわかります(ベクトルの端から見た場合、反時計回りに配置します)。 奇妙なことに(または、もちろん)、この方法にも3つの数字が必要です。 ベクトルの長さは重要ではないため、単位長にすることができます。 次に、それを設定するには、2つの数値(たとえば、OXとOYに対して相対的な2つの角度)だけが必要です。 これらの2つの数値に、ベクトルに対して回転する角度が追加されます。 これらのパラメーターを使用した回転行列の式は、 Wikipediaにも記載されています。
それだけです、ご清聴ありがとうございました。
PS記事を準備する過程で、PNGで600 dpiから保存されているように見えますが、数式は少しぼやけているように見えました。 Inkscapeは小さなpngを保存します。 私はこれを大いに謝りますが、やり直す力はありません。
PPS写真はhabrastorageにアップロードされますが、表示されない場合もあります。 どうやらhabrastorageのいくつかの問題。 ページをリロードしてみてください