👨🏿‍🌾 ☄️ 🏇🏻 数学、STA？!! 1 👣 👩🏾‍🏫 🌯

2012年の初め、CodeMash に関するHarry Bernhardtのレポート「WAT」のビデオ録画は、インターネットをサーフィンしていました。 habrには、このレポートについて2つのhabrastatyさえありました： one 、 two 。このプレゼンテーションでは、非論理的で反応を引き起こすRubyとJavaScriptの微妙な点のいくつかについて説明しました。「WAT？」。

同じhabrastatiで、数学的な推論の10個の例を収集しましたが、逆に一見すると論理的に見えますが、結果を見て、「STA？!!」という質問もしたいと思います。

だから、あなたはキャッチがどこにあるかを決定できますか？

1.学校の全員が算術級数の最初のnメンバーの合計の式を渡し、この式を最初のn個の正の整数の合計に適用します：

1 + 2 + 3 + ... + n = n （ n + 1）/ 2。

この式が1からn -1までの数の合計に適用されると、もちろん

1 + 2 + 3 + ... +（ n -1）=（ n -1） n / 2。

最後の等式の両方の部分に1つずつ追加しましょう。

1 + 2 + 3 + ... +（ n -1）+ 1 =（ n -1） n / 2 + 1。

簡略化すると、以下が得られます。

1 + 2 + 3 + ... + n =（ n -1） n / 2 + 1。

したがって、最初に書いたこの平等の左側の合計は何ですか？

n （ n + 1）/ 2 =（ n -1） n / 2 + 1。

ブラケットを開きます：

n ^2/2 + n / 2 = n 2/2- n / 2 + 1。

単純化して入手する

n = 1。

nは任意であるため、すべての正の整数が1であることを示しました。

STA？!!! 1

実際、この等式は偽です：

1 + 2 + 3 + ... +（ n -1）+ 1 = 1 + 2 + 3 + ... + n

これは代わりに顕著になります

1 + 2 + 3 + ... +（ n -1）

書く

1 + 2 + 3 + ... +（ n -3）+（ n -2）+（ n -1）

それから

1 + 2 + 3 + ... +（ n -3）+（ n -2）+（ n -1）+ 1 = 1 + 2 + 3 + ... +（ n -3）+（ n -2）+ n 、

もちろん等しくない

1 + 2 + 3 + ... + n

2.積分を考慮する

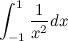$\ int _ {-1} ^ 1 \ frac {1} {x ^ 2} dx$ 。

関数1 / x ^2は定義のドメイン全体で正であるため、積分の値は正でなければなりません。見てみましょう。

関数1 / x ² の逆導関数は、逆導関数テーブルにあり、-1 / x + constです。

Newton-Leibniz式を使用します。

$\ int _ {-1} ^ 1 \ frac {1} {x ^ 2} dx =-\ frac {1} {x} + \ mathrm {const} \ Big | _ {-1} ^ 1 =-\ frac {1} {1} + \ frac {1} {-1} = -2$ 。

非常に正の数ではありません！

最初に、被積分関数が指定された間隔で連続している場合にのみ、ニュートン-ライプニッツの式が適用されます。ゼロでの関数には、第2種の不連続性があり、区間[-1、1]に制限されていません。（連続性の代わりに、より弱いプロパティのパフォーマンスを要求することができますが、いずれにしても、式は適用できません。）

3.連立方程式を考える

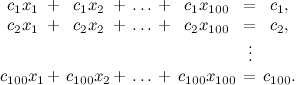
$\ begin {matrix} c_1x_1＆+＆c_1x_2＆+＆\ ldots＆+＆c_1x_ {100}＆=＆c_1、\\ c_2x_1＆+＆c_2x_2＆+＆\ ldots＆+＆c_2x_ s＆s＆s＆s＆s＆s＆s＆s＆s x_1＆+＆c_ {100} x_2＆+＆\ ldots＆+＆c_ {100} x_ {100}＆=＆c_ {100}。\ end {matrix}$

変数の数は方程式の数と一致するので、解がx _k =Δk /Δとして表されるという事実からなるCramer法を使用します。ここで、Δはシステムの行列の行列式であり、Δkは行列から得られる行列の行列式ですk番目の列を空きメンバー列に置き換えます。しかし、自由項の列は行列列のいずれかと一致するため、Δ=Δkです。したがって、すべてのkに対してx _k = 1です。さて、最初の方程式でこの解決策を代入してください：

$c_1 \ cdot1 + c_1 \ cdot1 + \ ldots + c_1 \ cdot1＆=＆c_1。$

したがって、100 c ₁ = c ₁です。等式の両側をc ₁で除算すると、100 = 1になります。

ワット？

Cramer法は、行列式Δがゼロ以外の場合にのみ適用できます。この場合、これはそうではありません。

4.シリーズを検討する

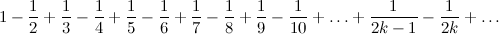
$1- \ frac12 + \ frac13- \ frac14 + \ frac15- \ frac16 + \ frac17- \ frac18 + \ frac19- \ frac1 {10} + \ ldots + \ frac1 {2k -1}-\ frac1 {2k} + \ ldots$

これは、いわゆる交互高調波級数であり、収束し、その合計はln 2です。

1つの負のメンバーの後に2つの負のメンバーが続くように、このシリーズのメンバーを再配置します。

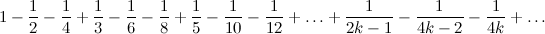
$1- \ frac12- \ frac14 + \ frac13- \ frac16- \ frac18 + \ frac15- \ frac1 {10}-\ frac1 {12} + \ ldots + \ frac1 {2k -1}-\ frac1 {4k -2} -\ frac1 {4k} + \ ldots$

ひどいことは何も起こらなかったようで、シリーズは収束も収束もしますが、このシリーズの部分和のサブシーケンスを見てみましょう。

$\ sum_ {k = 1} ^ {m} \左（\ frac1 {2k -1}-\ frac1 {4k -2}-\ frac1 {4k} \右）= \ sum_ {k = 1} ^ {m} \左（\ frac1 {4k-2}-\ frac1 {4k} \右）= \ frac12 \ sum_ {k = 1} ^ {m} \左（\ frac1 {2k-1}-\ frac1 {2k} \右）= \ frac12 \ sum_ {n = 1} ^ {2m} \ frac {（-1）^ {n + 1}} {n}$ 。

最後の合計は、最初の交互高調波系列の最初の2 m個のメンバーの合計にすぎず、その合計はln 2に等しいことを意味します。これは、並べ替えられた項を持つ系列の合計が½ln2に等しいことを意味します。

ln2 = ln2 / 2はどうですか？

シリーズは条件付きで収束したため、メンバーが再配置されたときに合計が変更されないことを保証できません。さらに、リーマンの定理は、この系列（および他の条件付き収束）から、用語の適切な順列により、事前に任意の数が合計される系列、または一般に発散系列を得ることができると述べています。

5.制限に移りましょう。制限を考慮する

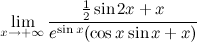$\ lim_ {x \ to + \ infty} \ frac {\ frac12 \ sin {2x} + x} {e ^ {\ sin {x}}（\ cos {x} \ sin {x} + x）}$ 。

分子と分母は無限大になる傾向があり、 xは無限大になる傾向があり、分子と分母も微分可能であるため、ロピタル規則を適用できます。

分子の導関数を見つける：

（½sin2x + x ） '= cos2 x + 1 = 2cos ² x 。

分母の導関数を見つける：

（e ^{sin x} （cos x sin x + x ）） '= e ^{sin x} cos x （cos x sin x + x ）+ e ^{sin x} （−sin ² x + cos ² x + 1）= e ^{sin x} cos x （cos x sin x + x + 2cos x ）。

どこから

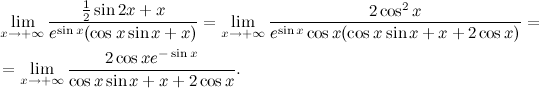
$\ begin {align *}＆\ lim_ {x \ to + \ infty} \ frac {\ frac12 \ sin {2x} + x} {e ^ {\ sin {x}}（\ cos {x} \ sin {x } + x）} = \ lim_ {x \ to + \ infty} \ frac {2 \ cos ^ 2x} {e ^ {\ sin {x}} \ cos {x}（\ cos {x} \ sin {x } + x + 2 \ cos {x}）} = \\＆= \ lim_ {x \ to + \ infty} \ frac {2 \ cos {x} e ^ {-\ sin {x}}} {\ cos {x} \ sin {x} + x + 2 \ cos {x}}。 \ end {align *}$

ここで、分子は有界関数であり、分母はxが無限大になる傾向があるので、分母は無限大になる傾向があるため、制限は0です。

異常なことに気がつかなかった場合は、元の制限の分母を次のように書き換えましょう。

e ^{sin x} （cos x sin x + x ）= e ^{sin x} （½sin2x + x ）。

したがって、元の関数の分子と分母は½sin2x + xだけ単純に削減できるため、限界符号の下の関数はe ^{-sin x}と単純に等しくなります。しかし、そのような関数にはすでにxに無限大が加えられているという制限はありません！

ねえ、なぜロピタルのルールは0になったのですか？！

ラピタルの定理の定式化では、限界を考慮するポイントのパンクチャされた近傍で分母が0にならないという要件もあります。この要件はここでは満たされていません。

この例を、D。Gruntzの論文「シンボリックマニピュレーションシステムの計算限界について」から取りました。

6.別の制限を次に示します。

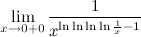$\ lim_ {x \ to 0 + 0} \ frac {1} {x ^ {\ ln \ ln \ ln \ ln {\ frac1x}-1}}$ 。

限界記号の下の関数グラフを見てみましょう。

(%i14) plot2d(1/x^(log(log(log(log(1/x)))) - 1), [x, 0, 0.01]);

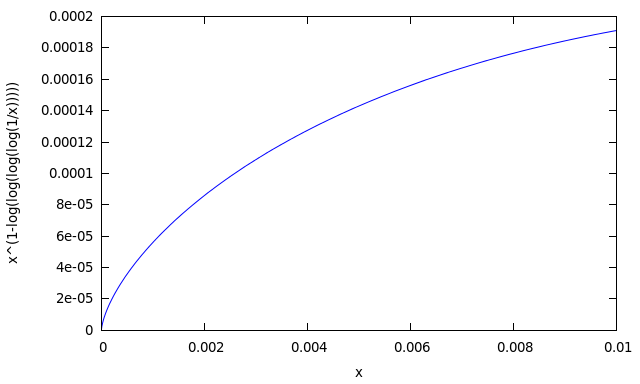
xが右側にゼロになる傾向がある関数はゼロになる傾向があることがわかります。確実性のためにいくつかの値を数えましょう：

 (%i47) f(x) := 1/x^(log(log(log(log(1/x)))) - 1)$ (%i48) f(0.00001); (%o48) 2.7321447178155322E-6 (%i49) f(0.0000000000000001); (%o49) 9.6464144195334194E-13 (%i50) f(10.0^-20); (%o50) 7.8557909648538576E-15 (%i51) f(10.0^-30); (%o51) 1.0252378366509659E-19 (%i52) f(10.0^-40); (%o52) 2.8974935848725609E-24 (%i53) f(10.0^-50); (%o53) 1.4064426717966528E-28

したがって、制限はおそらく0です。記号的に計算します：

 (%i59) limit(1/x^(log(log(log(log(1/x)))) - 1), x, 0, plus); (%o59) inf

プラス無限大を得た！それが正解です。

そして今、あなたはただ私をだましている、私はスケジュールを見ました！

関数ln ln ln ln xを詳しく見てみましょう。この関数は増加しますが、プラス無限大の制限はプラス無限大に等しくなりますが、非常にゆっくりと増加します。たとえば、 x = e ^{e ^{e ^{e ¹⁰}}}で値10を取り、これは10 ^{10 ^{10 ^9565.6に}}ほぼ等しくなります。したがって、式ln ln ln ln 1 / x -1は、 xが右側に0になる傾向があるため、依然として無限になり、したがって、望ましい制限は無限に等しくなります。

この例を、D。Gruntzの論文「シンボリックマニピュレーションシステムの計算限界について」からも取り上げました。

7.マトリックスを検討する

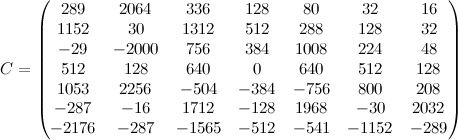$C = \左（\ begin {matrix} 289＆2064＆336＆128＆80＆32＆16 \ cr 1152＆30＆1312＆512＆288＆128＆32 \ cr -29＆-2000＆756＆384＆1008＆224＆48 \ cr 512＆128＆640＆0＆640＆512＆&&＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆＆ -512＆-541＆-1152＆-289 \ end {matrix} \右）$ 。

数学的パッケージを使用して、その固有値を見つけます。 Maximaが手元にあったので、それを利用しました。

 (%i162) load(lapack)$ (%i163) dgeev(C); (%o163) [[1.892759249004818 %i + 5.064646369950517, 5.064646369950517 - 1.892759249004818 %i, 4.316308825205465 %i + 1.156345532561647, 1.156345532561647 - 4.316308825205465 %i, - 5.560325596213962, 3.327556714595323 %i - 3.440829104405306, - 3.327556714595323 %i - 3.440829104405306], false, false]

つまり、およそ次の固有値を受け取りました。

-5.560、5.064 + 1.892 i 、5.064-1.892 i 、1.156 + 4.316 i 、1.156-4.316 i 、-3.440 + 3.327 i 、-3.440-3.327 i

さて、数字は数字ですが、転置した行列の固有値を見つけましょう。転置しても行列の固有値は変わらないため、同じ数字が得られるはずです。

 (%i164) dgeev(transpose(C)); (%o164) [[3.333252572558635 %i + 7.570309809213996, 7.570309809213996 - 3.333252572558635 %i, 7.453248893016916 %i + 1.804487379065658, 1.804487379065658 - 7.453248893016916 %i, 5.891112477041645 %i - 5.215502218450374, - 5.891112477041645 %i - 5.215502218450374, - 8.318589939657096], false, false]

つまり、転置行列の固有値はほぼ次のとおりです。

−8.318、7.570 + 3.333 i 、7.570-3.333 i 、1.804 + 7.453 i 、1.804-7.453 i 、-5.215 + 5.891 i 、-5.215-5.891 i 。

単一の試合ではありません！しかし、先に進み、象徴的に固有値を見つけましょう。

 (%i166) eigenvalues(C); (%o166) [[- 1, 1, - 2, 2, - 4, 4, 0], [1, 1, 1, 1, 1, 1, 1]]

今回は、-1、1、-2、2、-4、4、0を取得しました。

何も理解できませんでした！

実際、 C = L ⁻¹ R L 、ここで

$R = \ \ 0 0 0 0 0 0 \\ 0 0 0 0 0＆2＆2048 \\ 0 0 4・512・1024・256・64 \\ 0 0 0 0・512・512・128 \\ 0 0 0 0 -4＆1024 256 {pmatrixの} 1＆2 028・256・128・64・32・16 \\ 0 -2・1024・512・256・128・32 \\開始＆-1端{pmatrixの}$ 、

$R = \ begin {pmatrix} 1＆0＆0＆0＆0＆0＆0 \\ 0＆1＆0＆0＆0＆0＆0＆0＆\$ 。

したがって、正解は-1、1、-2、2、-4、4、0です。

この行列は固有値を見つける問題に関して条件が不十分であり、計算の誤差により、このような大きな誤差が得られるため、数値的手法は不正確な固有値を与えます。

固有値の条件数については、たとえばJ. Demmelの「計算線形代数」の本で詳しく読むことができます。この数値は、特定の固有値の左右の固有ベクトル間の鋭角の割線に等しいことにだけ注意してください。

このマトリックスの例を、S。K. Godunovのプレゼンテーション「計算線形代数のパラドックスと行列のスペクトルポートレート」から取りました。

8.平等について考えてみましょう。数学では最も美しいと考える人もいます。

e ^iπ + 1 = 0。

フォームに書き直します

e ^iπ = −1。

平等の両側を二乗することにより、

e ^{2 iπ} = 1。

そして今、私は最後の平等の両側を力iに上げます：

（e ^{2 iπ} ） ⁱ = 1 ⁱ 。

1は1に等しいことを知っているので、

e ^{2 i 2π} = 1。

しかし、 i ² = −1であることもわかっているため、

e ^−2π = 1。

ここでは、念のため、計算機を使用して、e-2πが0.001867442731708にほぼ等しく、これが1でないことを確認できます。

そして今回、キャッチは何ですか？

実際、複雑な度合いに引き上げる機能はあいまいであり、たとえば、

1 ⁱ = {e ^{−2π k} | k∈Z}。

したがって、4番目の移行はもはや真実ではありません。ブランチの1つだけを考慮すると、学位の通常の IDの一部が保持されなくなります。これがここで発生したことです。

9.長方形で構成される無限の長さの階段状プレートについて考えます。最初の長方形は1 cm x 1 cmの寸法の正方形で、2番目は0.5 cm x 2 cmの寸法の長方形で、次の長方形はそれぞれ2倍の長さで、2つはすでに前のものです2 ^{k -1 x} 2 ^{1- k} cmの測定値があります。各長方形の面積は1平方センチメートルなので、プレート全体の面積は無限です。したがって、このプレートをペイントするには無限のペイントが必要になります。

シリンダーで構成される容器を考えます。最初の円柱の高さは1 cm、半径も1 cm、2番目の円柱の高さは2 cm、半径は0.5 cmなどです。次の各円柱も前の円柱の2倍の長さで、半径は半分です。

この容器の容積を見つけます：シリンダーの容積は等比数列を形成します：π、½π、¼π、...、π/ 2 ^k 、...したがって、総容積は有限であり、2π立方センチメートルに等しくなります。

容器に塗料を塗ります。プレートを下げて引き出します。すべての面に有限量のペイントを使用して完全にペイントされます！

ワット？！

これは有名な画家パラドックスです。

プレートをペイントすることの不可能性について話したとき、プレートが同じ厚さのペイントの層で覆われていると仮定しました。

容器の助けを借りてペイントする場合、後続の各長方形は、ますます薄くなるペイント層で覆われます。

10.最後に、次のステートメントを証明します。

すべての馬は白です。

これを証明するために、誘導を使用します。

ベース誘導。 明らかに、白い馬がいます。これらの馬のいずれかを選択してください。

誘導ステップ。 k頭の馬が白であることを証明させてください。 k + 1頭の馬のセットを考えます。このセットから1頭の馬を削除します。残りのk頭の馬は誘導により白くなります。ここで、収納した馬を返し、他の馬を削除します。残りのk頭の馬は、誘導により再び白くなります。したがって、 k + 1頭の馬はすべて白になります。

したがって、すべての馬は白です。証明するために必要でした。

しかし、私は黒い馬を見ました！

ここではすべてが単純です：帰納法ベースでは、普遍的な量指定子の代わりに、存在量指定子が使用されます。

それでも推論の誤りを探したいなら、S。Klymchuk、S. Staples、“ Paradoxes and Sophisms in Calculus”をお勧めします。

数学、STA？!! 1

More articles: