位相平面z（x）での計算結果：
そしてy（x）：
曲線は閉じているように見えますが、結果をさらに詳しく見てみましょう。
使用した計算方法について簡単に
解析的数値的手法は、適応ステップ選択手順を備え、最大絶対局所誤差および合計計算誤差のレベルを制御する、可変次数の自己開始連続法に属します。
決定論的影響下にあるシステムの動的モデルを記述する通常の非線形非自律非定常積分微分方程式を解くために使用されます。
計算では、目的の解の正規成分はテイラー級数の形式で表されます。
動的システムのモデルを記述するODEシステムを解く際に分析数値法を適用した結果は、近似解だけでなく、正確な解を含むことが保証された領域でもあります。
つまり、近似解の数値に加えて、結果として、各計算ステップでの制限合計計算誤差の上限推定値も取得されます。
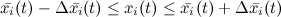
どこで
-近似解（i番目の位相座標）;
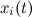-正確な解は不明。
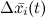-近似解の計算の限界総誤差の上限推定値;
決定論的影響下にあるシステムの動的モデルを記述する通常の非線形非自律非定常積分微分方程式を解くために使用されます。
計算では、目的の解の正規成分はテイラー級数の形式で表されます。
動的システムのモデルを記述するODEシステムを解く際に分析数値法を適用した結果は、近似解だけでなく、正確な解を含むことが保証された領域でもあります。
つまり、近似解の数値に加えて、結果として、各計算ステップでの制限合計計算誤差の上限推定値も取得されます。
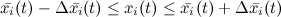
どこで
-近似解（i番目の位相座標）;
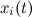-正確な解は不明。
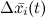-近似解の計算の限界総誤差の上限推定値;
記事「Lorentz Dynamic System and Computational Experiment」から計算のパラメーターを取得する：
前提条件、動的システムのパラメーター、数学演算の精度は小数点以下180桁、べき級数の精度は1e-9、ポイントt = 6.827で次の結果が得られます。
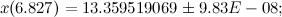
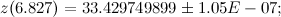
デリバティブ値：
計算結果がこの記事に記載されている結果と多少異なることは簡単にわかります。
さらに、記事の結果（解の近似値が見つかった）を元の方程式系に代入すると、記事に示されているものとは異なる導関数の値が得られます。
計算の精度（考慮される小数点以下の桁数とべき級数の精度）を高めると、正確な解を含む領域が狭くなることに注意してください。 たとえば、精度1e-55を設定すると、ポイントt = 6.827の面積は次のように狭くなります。
。
さらに、ポイントt = 12.827まで計算を続行し、位相平面z（x）上の計算結果のグラフを検討することにしました。
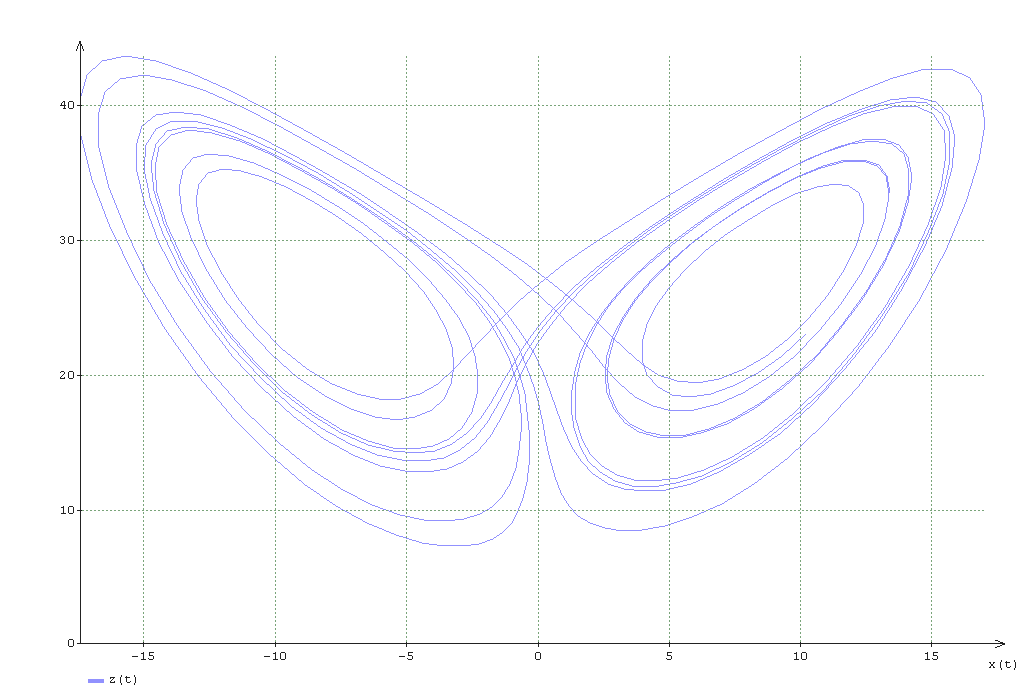
そしてy（x）：
グラフは、曲線が閉じていないことを明確に示しています。 より正確に言うと、最初のグラフでは閉じていません。位相軌跡が表示されるスケールだけでは、開いた点を見ることができません。
したがって、出発点付近への軌道の戻りについて話すことはできません。これは記事に記載されています。 そして、計算の誤差（方法論と計算の両方）を考慮して、計算に基づいて結論を出すことが常に必要です。
参照：
1. Bychkov Yu。、Scherbakov S.動的システムを計算するための解析的数値的方法。 -サンクトペテルブルク：Energoatomizdat、2001年。