(10進表記で記録された国のエリアの最初の桁)
一見無意味な統計指標を見てみましょう。 世界のすべての国の人口を10進表記で記述し、1から9までの各数字がこれらの数字の最初の数字である頻度を確認します。
結果は次のとおりです(人口はWikipediaから取得されました)。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.265 | 0.176 | 0.134 | 0.093 | 0.089 | 0.081 | 0.044 | 0.069 | 0.049 |
奇妙な単調さがすでに見えています。 明確にするために、グラフを作成します。

それは驚くべき結果でした。 10進数システムは単なるツールであり、区別されるものでも基本的なものでもないため、計算された分布は無意味で、目に見える規則性はありませんが、明確な単調さが見られます。
これまでのところ、これは根本的な理由のない事故と考えられるかもしれません。 いくつかの9個の数字が突然、なんとなく順序付けられたことが判明しました(7個の周波数は8個と9個の周波数よりも低くなっています)。
次に、別の地理的指標である世界の国々のエリアで同様の手順を実行しましょう。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.298 | 0.183 | 0.109 | 0.115 | 0.068 | 0.075 | 0.063 | 0.041 | 0.048 |
それもプロットしましょう
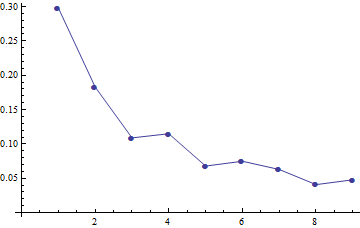
単調性はまだ完全ではありませんが、明らかに顕著です。
これは何らかの一般的なパターンですか? アメリカの州の地域を見てみましょう

まあ、そのようなわいせつな単調さはもはや観察されません。 これは、パターンの起源を示唆しています。 世界の国々の地域と人口は歴史の中で積極的に変化していますが、州の地域はかつて人為的に決定されており、自然な変化はありませんでした。単調である可能性が最も高いのは、これらの値が人口の規模および面積と著しく相関しているという事実によるものです。 最後に説明に戻ります。
数学的説明
同様のインジケーター-等比数列の10進表記の最初の桁の頻度-1,2,4、...、2 nを検討してください。 n = 1000とすると、次のようになります。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.301 | 0.177 | 0.124 | 0.097 | 0.080 | 0.067 | 0.057 | 0.052 | 0.044 |
同様のパターンが見られます-単調で、ユニットは9よりも数倍頻繁に見つかります。 この事実には厳密な数学的証明があります。 この記事では、それ自体は興味深いものですが、あまり重要ではありません。
証明 
定理の証明
したがって、限界では次の結果が得られます。
これらの周波数が進行の分母の選択から独立していること自体は驚くべきことです。

定理の証明
したがって、限界では次の結果が得られます。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| lg 2 | lg 3/2 | lg 4/3 | lg 5/4 | lg 6/5 | lg 7/6 | lg 8/7 | lg 9/8 | lg 10/9 |
| 0.301 | 0.176 | 0.125 | 0.097 | 0.079 | 0.067 | 0.058 | 0.051 | 0.046 |
これらの周波数が進行の分母の選択から独立していること自体は驚くべきことです。
私が知る限り、次の推論のアイデアは偉大な数学者V.I.アーノルドに属します。
そのため、等比数列の数字の最初の桁が同様の分布に従うことを確立しました。 この接続は今どのように説明できますか? アーノルドは、ここでのポイントはこのシステムのエルゴード性(この概念に関する視覚的なメモ )、つまり、空間平均値(ここでは計算した統計のみ)は、空間のあるポイントでの一時的な平均値(つまり、長期にわたる1つの国の人口の値について同様の統計が取られます)。 ここでいう空間とは、フェーズ空間-多くの国です。 この場合、それは次のように解釈できます:現在の世界のすべての国は歴史を通じて同じ国の発展の段階と見なすことができます、この対応は非常に不正確です、現在の世界の国の人口のセットはある国の人口のセットとしばらく一致しませんただし、調査する平均値は同じです。
したがって、タスクは1つの国の人口動態の研究に限定されました。 幾何学的な進行によって既に近似できます。 局所的にはもちろん、この近似は非常に不正確ですが、数値の最初の桁は数値の小さな変化にあまり敏感ではないパラメーターです。したがって、長期間にわたって母集団のダイナミクスが指数関数に似ている場合、最初の桁の頻度分布は理論的に得られた頻度分布に似ています。
この現象を示すグラフを次に示します。

さて、集団に対して観察された効果を説明することができました。 正方形はどうですか?
スクエア
それらは、指数関数的に成長しているとはもはや言えません。 ここでは、そのような数学的モデルを提供できます。世界は、同じ規模の特定の国から始まります。 各時間単位で、2つのイベントのいずれかが等しく発生する可能性があります。ランダムに選択された国が2つの同一エリアに分割されるか、同じエリアの2つのランダムに選択された国が1つに結合されます。 このモデルは厳密な数学的研究を可能にしますが、この記事のトピックからはすでに非常に遠いため、ここでは説明しません。 そうであっても、そのようなモデルは同様の頻度分布につながります。
しかし、彼女は現実にあまり似ていません。 はい、世界では、国は時々団結し、時には半分に分割されますが、面積比は固定からはほど遠いものであり、原則として、共通の国境を持つ国のみが団結します。 これらすべての要因を考えると、モデルを改善することは可能ですが、数学にとってはすでに耐えられません(これは私の個人的な意見であり、おそらく誰かがこの方向でまともな結果を得ることができました)。
ここでは、コンピューターシミュレーションが役立ちます。 私はこのモデルを選択しました。世界は長方形であり、国は側面が世界の側面に平行な長方形です。 確率pの時間単位では、共通の側面を持つ2つの国が1つに統合され、確率(1-p)で1つの国が直線で2つに分割されます。
実装のために、最初に手に入れたものを選択したので、選択がおかしいと思われる場合は申し訳ありません。 これは、pygameモジュールを使用したPython 2.7です。
コード(結果のみに記述されているため、非常に無駄がありません)
import pygame import random import time cell_size = 10 WIN_WIDTH = 850 WIN_HEIGHT = 850 BACKGROUND_COLOR = "#D3D3D3" DISPLAY = (WIN_WIDTH, WIN_HEIGHT) p = 0.3 class Country(object): def __init__(self, x, y, dx, dy): self.x = x self.y = y self.dx = dx self.dy = dy self.color = (random.choice(range(256)), random.choice(range(256)), random.choice(range(256))) def get_neighbs(self, countries): self.neighbors = [] for i in range(len(countries)): c = countries[i] if cx == self.x and c.dx == self.dx and (cy + c.dy == self.y or cy == self.y + self.dy): self.neighbors.append(i) if cy == self.y and c.dy == self.dy and (cx + c.dx == self.x or cx == self.x + self.dx): self.neighbors.append(i) def __repr__(self): return str((self.x, self.y, self.dx, self.dy, self.neighbors)) __str__ = __repr__ def draw(self, screen): self.image = pygame.Rect(self.x, self.y, self.dx, self.dy) pygame.draw.rect(screen, self.color, self.image) def area(self): return self.dx * self.dy def world_init(): countries = [Country(50, 50, 250, 250), Country(300, 50, 250, 250), Country(550, 50, 250, 250), Country(50, 300, 250, 250), Country(300, 300, 250, 250), Country(550, 300, 250, 250), Country(50, 550, 250, 250), Country(300, 550, 250, 250), Country(550, 550, 250, 250)] for c in countries: c.get_neighbs(countries) return countries def merge(countries, i, j): """i < j""" if countries[i].x < countries[j].x: new_country = Country(countries[i].x, countries[i].y, countries[i].dx + countries[j].dx, countries[i].dy) if countries[i].y < countries[j].y: new_country = Country(countries[i].x, countries[i].y, countries[i].dx, countries[i].dy + countries[j].dy) if countries[i].x > countries[j].x: new_country = Country(countries[j].x, countries[j].y, countries[j].dx + countries[i].dx, countries[j].dy) if countries[i].y > countries[j].y: new_country = Country(countries[j].x, countries[j].y, countries[j].dx, countries[j].dy + countries[i].dy) del countries[i] del countries[j - 1] countries.append(new_country) for c in countries: c.get_neighbs(countries) def divide(countries, i, midx=0, midy=0): print countries[i].area() if midy == 0: new1 = Country(countries[i].x, countries[i].y, midx, countries[i].dy) new2 = Country(countries[i].x + midx, countries[i].y, countries[i].dx - midx, countries[i].dy) del countries[i] countries.append(new1) countries.append(new2) for c in countries: c.get_neighbs(countries) if midx == 0: new1 = Country(countries[i].x, countries[i].y, countries[i].dx, midy) new2 = Country(countries[i].x, countries[i].y + midy, countries[i].dx, countries[i].dy - midy) del countries[i] countries.append(new1) countries.append(new2) for c in countries: c.get_neighbs(countries) def world_draw(countries, screen): for c in countries: c.draw(screen) def random_action(countries): rand = (random.uniform(0, 1) < p) if rand: i = random.choice(range(len(countries))) if countries[i].neighbors: j = random.choice(countries[i].neighbors) merge(countries, i, j) else: i = random.choice(range(len(countries))) xaxis = random.choice([True, False]) if xaxis: try: mid = random.choice(range(cell_size, countries[i].dx, cell_size)) except IndexError: return 0 divide(countries, i, midx=mid) else: try: mid = random.choice(range(cell_size, countries[i].dy, cell_size)) except IndexError: return 0 divide(countries, i, midy=mid) def get_stat(countries): digits = [int(str(c.area())[0]) for c in countries] result = {0:0.0, 1:0.0, 2:0.0, 3:0.0, 4:0.0, 5:0.0, 6:0.0, 7:0.0, 8:0.0, 9:0.0} for d in digits: result[d] += 1 for d in range(1, 10): result[d] = round(result[d] / len(digits), 3) return result def main(): pygame.init() screen = pygame.display.set_mode(DISPLAY) pygame.display.set_caption("World History") bg = pygame.Surface((WIN_WIDTH, WIN_HEIGHT)) bg.fill(pygame.Color(BACKGROUND_COLOR)) countries = world_init() waiting = True while waiting: events = pygame.event.get() for event in events: if event.type == pygame.KEYDOWN: if event.key == pygame.K_SPACE: waiting = False for i in range(1000): for e in pygame.event.get(): if e.type == pygame.QUIT: raise SystemExit, "QUIT" world_draw(countries, screen) pygame.display.update() random_action(countries) time.sleep(0.07) print get_stat(countries) main()
これがプログラムのビデオです(1000回の反復があります)。
1000回の繰り返しでは、統計値はまだ理論値と完全には一致していませんが、10000ではすでに近い値になっています。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.435 | 0.226 | 0.106 | 0.085 | 0.045 | 0.038 | 0.020 | 0.029 | 0.015 |
これらのデータは、p = 0.3で得られました。 pの異なる値と世界の初期構成を試してみると、十分な数の反復でどこでも同様の結果が得られるため、明らかに、考慮中の条件はこのタイプのすべてのモデルに共通です
したがって、そのような一見無意味な実験的事実は、数論や力学系の理論のような数学の深い部分に私たちを導いた
PSこの記事の数学的な部分のアイデアは、V.I。Arnoldによる人気の科学記事から得たもので、一度読んだことがありますが、残念ながら今は見つかりませんでした。