 古い灰色のロバEeyoreは森の草に覆われたアザミの角に一人で立ち、足を大きく離し、頭を片側にぶら下げ、重大なことを考えました。
古い灰色のロバEeyoreは森の草に覆われたアザミの角に一人で立ち、足を大きく離し、頭を片側にぶら下げ、重大なことを考えました。
A.ミルン「くまのプーさんとすべてすべて」
-ロバを見ますか? 警官に尋ねます。 -そこに小さな灰色のロバがいます...記事2908。価格は32コペックです。 彼には素晴らしい未来があります。
「ロバはこれを行う」と警官は同意する。 -彼らは時々非常に素晴らしい未来を持っています。
ヘンリー・アルトフ「ロバと公理」
ボードゲームの開発で最も難しい部分は何ですか? 明らかに、ボード上でピースを動かすアニメーションではありません。 合理的で興味深いゲームルールを考案するのは困難です。 ゲームのバランスを確保することは非常に困難です。 コンピューター開発に携わっている場合、高品質のAIを実装するのはめったに困難です(囲Goや将giなどのゲームでは、この問題はこれまで解決されていません)。 そして、たとえ機能するAIを実装できたとしても、その作業の品質を評価し、いくつかの可能なオプションから最適なものを選択するために、非常に多くの作業を行う必要があります。
これらすべての問題に対するソリューションを大幅に簡素化できるツールについてお話したいと思います。 Axiom Development Kitは 、 Zillions of Gamesを改善する方法として開発者によって考案されました。 特に、AI ZoGが非常に貧弱な領域の発作に関連するゲーム(Goなど)の実装に焦点を当てています。 さらに、AxiomはZoG開発者の機能を大幅に拡張し、従来のZRF(ルール記述言語)のフレームワークでは実際には実現されない多くの機会を提供します。 これにより、Axiomは、ZoGがコンピューターにインストールまたは購入されたことがない場合でも、完全に独立して動作できます。 しかし、まず最初に...
画像で
ZoGには多くの欠点があることをすでに書きました。 幸いなことに、開発者はそれらのいくつかに対処するメカニズムを提供しています。 拡張モジュール(エンジン)は、視覚化を除くゲームのあらゆる側面を制御する動的にロードされるライブラリ(DLL)です。 ここでは、そのような拡張の例を見ることができます。
独自の拡張機能を自分で開発するには、非常に時間がかかる場合があります。 エンジンを接続すると、通常のZoG AIが無効になるため、AIを開発する必要があります(ほとんどの場合、C ++で)。 Axiomは、AIアルゴリズムなど、開発者にとって難しいものを実装するプログラム可能なエンジンであり、ゲームロジックに集中する機能を提供します。
Royal Game of Urを実装してみましょう。 動作するには、最小限のZRFファイルが必要です。
エンジン接続
(version "2.0") (game (title "Ur") (engine "../Axiom/Ur/axiom.dll") (option "animate captures" false) (option "animate drops" false) (option "show moves list" false) (option "pass turn" forced) (option "highlight goals" false) (option "prevent flipping" true) (option "recycle captures" true) (drop-sound "Audio/Dice_cup.wav") (move-sound "Audio/Clack.wav") (capture-sound "") (players Black White ?Dice) (turn-order White ?Dice ?Dice ?Dice ?Dice Black ?Dice ?Dice ?Dice ?Dice) (board (image "Images\Ur\board.bmp") (grid (start-rectangle -503 -13 -442 79) (dimensions ("a/b/c/d/e/f/g/h/i/j/k/l/m/n/o/p/q" (67 0)) ; files ("5/4/3/2/1" (0 66)) ; ranks ) ) ) (board-setup (?Dice (wdice q4) (bdice q3 q2) (lock q1) ) (Black (init i5 j5 k5 l5 m5 n5 o5) ) (White (init i1 j1 k1 l1 m1 n1 o1) ) ) (piece (name lock) (image ?Dice "Images\Ur\invisible.bmp" Black "Images\Ur\invisible.bmp" White "Images\Ur\invisible.bmp") ) (piece (name init) (image Black "Images\Ur\binit.bmp" White "Images\Ur\winit.bmp") ) (piece (name prom) (image Black "Images\Ur\bprom.bmp" White "Images\Ur\wprom.bmp") ) (piece (name wdice) (image ?Dice "Images\Ur\wdice.bmp") ) (piece (name bdice) (image ?Dice "Images\Ur\bdice.bmp") ) ; The following dummy piece is required in order to placate the Zillions engine. ; It appears as though Zillions must find at least one "moves" keyword somewhere ; in the zrf in order for it to be happy and thus allow "moves" to work correctly. (piece (name Dummy) (dummy) (moves (from))) )
ここにプレイヤーの説明、動きのシーケンス、ピースがありますが、ピースが行くルールの説明はありません。 また、ボード上の方向、ゲームゾーン、ゲームを終了する条件、およびゲームルールに関連する他のすべての定義はありません。 これらはすべて公理スクリプトに含まれます。 悲しい点は、エンジンとのZoGインターフェースは、ZRFファイルに含まれる情報の転送を提供しないことです。 つまり、これらの説明はすべてAxiomスクリプトで複製する必要があります。
幸いなことに、Axiom Development Kitには、このプロセスを自動化するユーティリティが付属しています。 ZRF Converterは非常に機嫌が悪いです。 ZRFファイル内の何か(たとえば、マクロ内のボードの説明)が気に入らなかった場合、変換プロセスが中断され、頭を痛める不思議な診断が行われます。 すべてがうまくいった場合、出力に次の説明が表示されます。
Ur.4th
{board {position} a5 {position} b5 {position} c5 {position} d5 {position} e5 {position} f5 {position} g5 {position} h5 {position} i5 {position} j5 {position} k5 {position} l5 {position} m5 {position} n5 {position} o5 {position} p5 {position} q5 {position} a4 {position} b4 {position} c4 {position} d4 {position} e4 {position} f4 {position} g4 {position} h4 {position} i4 {position} j4 {position} k4 {position} l4 {position} m4 {position} n4 {position} o4 {position} p4 {position} q4 {position} a3 {position} b3 {position} c3 {position} d3 {position} e3 {position} f3 {position} g3 {position} h3 {position} i3 {position} j3 {position} k3 {position} l3 {position} m3 {position} n3 {position} o3 {position} p3 {position} q3 {position} a2 {position} b2 {position} c2 {position} d2 {position} e2 {position} f2 {position} g2 {position} h2 {position} i2 {position} j2 {position} k2 {position} l2 {position} m2 {position} n2 {position} o2 {position} p2 {position} q2 {position} a1 {position} b1 {position} c1 {position} d1 {position} e1 {position} f1 {position} g1 {position} h1 {position} i1 {position} j1 {position} k1 {position} l1 {position} m1 {position} n1 {position} o1 {position} p1 {position} q1 board} {players {player} Black {player} White {player} ?Dice {random} players} {pieces {piece} lock {piece} init {piece} prom {piece} wdice {piece} bdice {piece} Dummy pieces} {turn-order {repeat} {turn} White {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} Black {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} ?Dice turn-order} {board-setup {setup} ?Dice wdice q4 {setup} ?Dice bdice q3 {setup} ?Dice bdice q2 {setup} ?Dice lock q1 {setup} Black init i5 {setup} Black init j5 {setup} Black init k5 {setup} Black init l5 {setup} Black init m5 {setup} Black init n5 {setup} Black init o5 {setup} White init i1 {setup} White init j1 {setup} White init k1 {setup} White init l1 {setup} White init m1 {setup} White init n1 {setup} White init o1 board-setup}
ここで最初の驚きが待っています。 Axiomでは、ボードをよりコンパクトに記述できますが、重大な制限があります。 グリッドデザインでは、「標準」セル名を持つ長方形のボードのみを記述できます(さらに、ボードの説明ではグリッドを1つだけ使用できます)。 より複雑な形状(3次元など)のボードを記述する必要がある場合は、ZRFコンバーターと同じ方法で各位置を明示的に記述する必要があります。 この場合、すべての制限が尊重されるため(ZRF実装と比較して、ボードの列と行の名前を変更する必要がありました)、よりコンパクトなレコードを使用します。
{board 5 17 {grid} board}
次に、数字が移動できる方向を決定する必要があります。 ChessやCheckersなどのゲームでは、座標の増分に関して方向を定義するコンパクトな表記法を使用できます。
{directions -1 0 {direction} North 1 0 {direction} South 0 1 {direction} East 0 -1 {direction} West -1 1 {direction} Northeast 1 1 {direction} Southeast -1 -1 {direction} Northwest 1 -1 {direction} Southwest directions}
悲しいかな、私たちの場合、この方法は適切ではありません。 ウルのゲームでは、ボード上のチップの動きの軌跡は非常に奇妙なので、位置間の関係を明確に決定する必要があります。
道順
{directions ( Anext ) {link} Anext i1 l2 {link} Anext j1 l2 {link} Anext k1 l2 {link} Anext l1 l2 {link} Anext m1 l2 {link} Anext n1 l2 {link} Anext o1 l2 {link} Anext l2 k2 {link} Anext k2 j2 {link} Anext j2 i2 {link} Anext i2 i3 {link} Anext i3 j3 {link} Anext j3 k3 {link} Anext k3 l3 {link} Anext l3 m3 {link} Anext m3 n3 {link} Anext n3 o3 {link} Anext o3 o2 {link} Anext o2 p2 {link} Anext p2 p3 {link} Anext p3 p4 {link} Anext p4 o4 {link} Anext o4 o3 ( Bnext ) {link} Bnext i5 l4 {link} Bnext j5 l4 {link} Bnext k5 l4 {link} Bnext l5 l4 {link} Bnext m5 l4 {link} Bnext n5 l4 {link} Bnext o5 l4 {link} Bnext l4 k4 {link} Bnext k4 j4 {link} Bnext j4 i4 {link} Bnext i4 i3 {link} Bnext i3 j3 {link} Bnext j3 k3 {link} Bnext k3 l3 {link} Bnext l3 m3 {link} Bnext m3 n3 {link} Bnext n3 o3 {link} Bnext o3 o4 {link} Bnext o4 p4 {link} Bnext p4 p3 {link} Bnext p3 p2 {link} Bnext p2 o2 {link} Bnext o2 o3 ( Cnext ) {link} Cnext p3 p4 {link} Cnext p4 o4 {link} Cnext o4 o3 {link} Cnext o3 n3 {link} Cnext n3 m3 {link} Cnext m3 l3 {link} Cnext l3 k3 {link} Cnext k3 j3 {link} Cnext j3 i3 {link} Cnext i3 h3 ( Dnext ) {link} Dnext p3 p2 {link} Dnext p2 o2 {link} Dnext o2 o3 {link} Dnext o3 n3 {link} Dnext n3 m3 {link} Dnext m3 l3 {link} Dnext l3 k3 {link} Dnext k3 j3 {link} Dnext j3 i3 {link} Dnext i3 h3 directions}
黒と白のチップの動きは異なるため、白の場合はAnext 、黒の場合はBnextの方向を決定する必要がありました。 さらに、変換フィールドを通過したチップについては、 CnextおよびDnextの方向を決定する必要があります 。 これが行われない場合、フォークがo3フィールド上に形成され、すべてのチップが小さなブロック内で円形に回転し、利用可能な最初のルートを選択します。
{symmetries Black {symmetry} Anext Bnext Black {symmetry} Cnext Dnext symmetries}
この設計により、「対称性」を定義できます。 良い例は、チェスのポーンの動きです。 ポーンは常に前方に移動しますが、白の場合はボードを上に移動し、黒の場合は反対方向に移動します。 より複雑な対称形式があります。 たとえば、チェスの4辺の変形では、色に応じて「前方」への移動は、4つの「基本ポイント」のいずれかの方向に発生する可能性があります。 「対称性」を定義したら 、図の色に注意を払わずに、常に同じ方向(たとえばAnext )を使用できます。 黒の場合、自動的に対称( Bnext )に変換されます。
要塞
フォートとの知り合いは早かったが、非常に長い間気まぐれのままだった。 フォートを初めて見たのは、BC-ShekとMikroshのときでした。 私の友人にはVector 06Cがあり 、すべての親の共同の努力により、耳からのみ成功しました。 Vektorには、ゲームの入ったカセットが時々購入され、「不明」が時々発見されました。 そのような原因不明の中で、フォートの実装が見つかりました。 友人とスタックで十分に遊んだので、友人と私は「aha」と言って、数字体系の基礎をゼロに設定しました(Fortにはとても楽しい機会があります)。 砦は当然これに耐えることができず、しばらく忘れていました。
その後、すでに研究所で、フォートは私の注意の表面に繰り返し浮上しましたが、彼らはそれに真剣に対処することができませんでした。 実際、Fortのマイクロコントローラープログラミングやその他の便利なアプリケーションに出会う機会はありませんでした。 そして今、Axiom開発者のおかげで、私にはそのような機会があります! 実際には、Forthという単語が理由でForthScriptに表示されます。 実際、Axiom自体とForthScriptの一部の両方がFortに実装されており、 axiom.dllにはそれらを使用できるインタープリターがあります。 必要に応じて、 axiom.4thおよびCORE.4THで実装の詳細を確認し、おそらく修正することができます。
したがって、すべてのゲームロジックをプログラミングするにはFortが必要です。 しかし、どこから開発を始めますか? 手始めに、ボード上のピースの簡単な動きを実現することは素晴らしいことです。 各図は、独自の軌道に沿って1、2、3、または4個のセルを移動できる必要があります(「骨」にランダムなポイントを投げて気を散らすまで)。
フィギュアの動き
: common-move ( 'dir n -- ) SWAP BEGIN DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move add-move ENDIF ; : i-move-1 ( -- ) ['] Anext 1 common-move ; : i-move-2 ( -- ) ['] Anext 2 common-move ; : i-move-3 ( -- ) ['] Anext 3 common-move ; : i-move-4 ( -- ) ['] Anext 4 common-move ; : p-move-1 ( -- ) ['] Cnext 1 common-move ; : p-move-2 ( -- ) ['] Cnext 2 common-move ; : p-move-3 ( -- ) ['] Cnext 3 common-move ; : p-move-4 ( -- ) ['] Cnext 4 common-move ; {moves i-moves {move} i-move-1 {move} i-move-2 {move} i-move-3 {move} i-move-4 moves} {moves p-moves {move} p-move-1 {move} p-move-2 {move} p-move-3 {move} p-move-4 moves} {pieces {piece} init {moves} i-moves {piece} prom {moves} p-moves pieces}
実行時にZRF-kuを実行すると、数字を移動できるようになります。 どのように機能しますか? common-moveの実装を見てみましょう。 名前の直後にあるコメント(フォートスタイル)は、スタック上の2つのパラメーター(コンパイル済みの方向遷移コマンドと移動ステップ数)を取ることを示しています。 実装自体は2つの部分で構成されています。 まず、指定された回数のサイクルで方向転換が実行され、次にターゲットフィールドが空であることを確認した後、移動(チップの移動)を形成する一連のAxiomコマンドが実行されます。 最も重要なことは、このバランスをとるすべての行為中に、スタックを破壊しないことです!
実行可能な各コマンドの説明は、Axiom Development KitにバンドルされているForthScriptおよびAxiomのマニュアルに記載されていますが、このコードとZRFを使用して記述できるものとのいくつかの重要な違いに注目してください。
- Axiomでは、方向遷移コマンド(上記のスクリプトではEXECUTEを使用して実行されます)は、遷移の成功を確認するために使用できるブールコードを生成します(特定のセルの方向が定義されていない場合、遷移は実行されず、 FALSEがスタックに配置されます)
- add-move完了コマンドは、move moveコマンドとは分離されています(これがなぜそんなに重要なのかを記事に書きました)。
このバージョンでしばらく遊んだ後、小さなブロックに到達したチップが円を描くようになっていることがわかります。 チップがこの「輪廻の輪」から抜け出すには、裏返しにする必要があります(裏返したチップについては、フィニッシュに至る方向CnextおよびDnextが与えられます)。 Urのゲームでチップを回すのは難しいことを思い出させてください。 チップは裏返され、変換フィールド上に立つのではなく、通過します。 さらに、チップは最後まで進むことができるので、フィニッシュに達したボードからチップを取り除くことを忘れないでください:
チップの反転
VARIABLE isPromouted : common-move ( 'dir n -- ) FALSE isPromouted ! SWAP BEGIN current-player White = IF here p2 ELSE here p4 ENDIF = IF TRUE isPromouted ! ENDIF DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move here h3 = IF capture ENDIF isPromouted @ IF current-piece-type 1+ change-type ENDIF add-move ENDIF ;
ここにフォートの変数に関するいくつかの言葉があります。 VARIABLEキーワードを使用してisPromouted変数を定義します。 変数が定義された後、コード内で変数が言及されると、この変数のアドレスがスタックにプッシュされます。 指定されたアドレスにある値を取得するには、 @コマンド、 ! 変数の値を上書きします。
Axiomの複雑さは、形状の種類の操作によって表されます。 実際のところ、図の定義は、それらの動きを制御するコードの後にあります(それらが使用されているため)。 このため、コードで形状のタイプの名前を使用することはできません(この時点ではまだ定義されていないため)。 原則として、この不快な状況から抜け出すことができます。 たとえば、コードでは、チップをフリップするために、移動を実行するピースのタイプを単純にインクリメントします。
ゲームプレイの重要な部分は、プレイヤーの動きをスキップする機能です。 プレーヤーは、可能であれば移動を完了し、それ以外の場合は移動をスキップする必要があります。 わざとこれを気にしない場合、ゲームはプレイヤーのいずれかによる最初の移動不可能性で引き分けで自動的に完了します。 また、相手のターンをスキップすることにより、「アウトレット」への移動の後にプレイヤーの2番目の移動を実装することは論理的です。 それをやってみましょう:
進捗をスキップ
: is-rosette? ( -- ? ) here i2 = here i4 = OR here l3 = OR here o2 = OR here o4 = OR ; : common-move ( 'dir n -- ) q5 enemy-at? NOT IF FALSE isPromouted ! SWAP BEGIN current-player White = IF here p2 ELSE here p4 ENDIF = IF TRUE isPromouted ! ENDIF DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move here h3 = IF capture ENDIF isPromouted @ IF current-piece-type 1+ change-type ENDIF is-rosette? IF q1 piece-type-at q5 create-piece-type-at ELSE q5 capture-at ENDIF add-move ENDIF ENDIF ; : pass-move ( -- ) q5 capture-at Pass add-move ; {moves i-moves {move} i-move-1 {move-type} normal-type {move} i-move-2 {move-type} normal-type {move} i-move-3 {move-type} normal-type {move} i-move-4 {move-type} normal-type {move} pass-move {move-type} pass-type moves} {moves p-moves {move} p-move-1 {move-type} normal-type {move} p-move-2 {move-type} normal-type {move} p-move-3 {move-type} normal-type {move} p-move-4 {move-type} normal-type {move} pass-move {move-type} pass-type moves} {move-priorities {move-priority} normal-type {move-priority} pass-type move-priorities}
is-rosetteのキャッチーな定義を最初にキャッチしましたか? 。 残念ながら、Axiomでは、ZRFとは異なり、ゲームゾーンを定義する方法はありません。 すべてのフィールドを個別にチェックする必要があります。
スキップの実装は、ZRFで使用されるアプローチとも異なります。 「パスターン」オプションの設定は、Axiomによって無視されます。 代わりに、 Passコマンドでスキップを明示的に構成する必要があります 。 これは、ZSGムーブ記録記法機能(エンジンからZoGにムーブを転送するために使用)のより完全な使用の一例です。 別のそのような例は、ZRFに実装されていない、部分的な移動を実行するときにドロップコマンドを使用する機能です。
ご注意
独自の拡張モジュール( エンジン )を開発する場合、ZSG表記法を理解することは非常に重要です。 ZoGで移動を実行する能力は、ZSG表記で記述できるかどうかによって完全に決定されます。 ZoGはこの形式を文書化しませんが、Axiomの文書にはそれを説明するセクションがあります(付録B)。 このセクションに精通していると、ZSG表記の機能を明確にするために、開発者が長時間の実験を行う必要がなくなります。
他の移動の可能性がない場合にのみパスが機能するためには、優先順位を使用する必要があります。 優先度の低い移動は、優先度の高い移動の可能性がない場合にのみ実行できます。 残念ながら、「パスターン」オプションをforceに設定する場合、AxiomスタイルのスキップはZoGの動作と機能的に完全に同等ではありません。 ZRF実装では、スキップは自動的に実行されます。Axiomの場合、ボタンをクリックする必要があります。
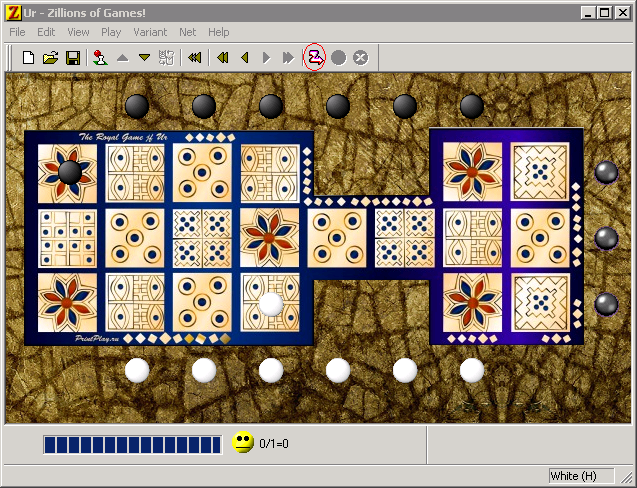
これは紛らわしいことです。
「アウトレット」への移動後にスキップ移動を実装するために、目に見えない図形ロックが位置q5に配置されますが、これはゲームでは使用されません。 common-moveの最初に、このフィールドに敵のフィギュアが存在するかどうかのチェックが行われます。 フィールドが敵に占領されている場合、移動することはできません。
さて、さいころを振る方法を学びましょう。
骨投げ
{players {player} White {player} Black {player} ?Dice {random} players} {turn-order {turn} White {turn} ?Dice {of-type} clear-type {turn} ?Dice {turn} ?Dice {turn} ?Dice {turn} Black {turn} ?Dice {of-type} clear-type {turn} ?Dice {turn} ?Dice {turn} ?Dice turn-order} : drop-dices ( -- ) q2 here = q3 here = OR q4 here = OR empty? AND IF drop add-move ENDIF ; : count-dices ( -- n ) q2 piece-at piece-value q3 piece-at piece-value + q4 piece-at piece-value + DUP 0= IF DROP 4 ENDIF ; : clear-dices ( -- ) q1 here = verify q2 not-empty-at? q3 not-empty-at? q4 not-empty-at? AND AND IF drop q2 capture-at q3 capture-at q4 capture-at add-move ENDIF ; : i-move ( -- ) ['] Anext count-dices common-move ; : p-move ( -- ) ['] Cnext count-dices common-move ; {moves p-moves {move} p-move {move-type} normal-type {move} pass-move {move-type} pass-type moves} {moves drops {move} drop-dices {move-type} normal-type {move} pass-move {move-type} pass-type moves} {moves clears {move} clear-dices {move-type} clear-type moves} {pieces {piece} lock {moves} clears {piece} init {moves} i-moves {piece} prom {moves} p-moves {piece} wdice {drops} drops 1 {value} {piece} bdice {drops} drops 0 {value} pieces}
「ボーン」( drop-dices )のスローは基本的に実行されます。 ターゲットフィールドがサイコロを投げるためのものであることを確認し、 ドロップコマンドでシェイプを配置し、 add-moveコマンドで移動を終了します。 クリアダイスはもう少し複雑です。 ZoGでは、ボードからピースを取り除くだけで構成されるムーブを形成する方法はありません。 クリーニングプロセスを、ゲームで使用されていないq1フィールドに不可視の数字をリセットすることに関連付けます。 ボードから「骨」を取り除くことは、この動きの副作用です。 ドロップされたポイントをカウントし( count-dices )、この値をcommon-moveに渡します。
ゲームを終了する条件を決定するために、ボードを離れたチップを数える必要があります。 完了チェック自体は、オーバーライドされた単語OnIsGameOverを呼び出すことにより、Axiomによって実行されます。 ゲームの開始時に初期アクション(疑似乱数ジェネレーターの初期化など)を実行するには、 OnNewGameをオーバーライドする必要があります。
終了条件
{board 5 17 {grid} {variable} WhitePieces {variable} BlackPieces board} : WhitePieces++ WhitePieces ++ ; : BlackPieces++ BlackPieces ++ ; : common-move ( 'dir n -- ) q5 enemy-at? NOT IF FALSE isPromouted ! SWAP BEGIN current-player White = IF here p2 ELSE here p4 ENDIF = IF TRUE isPromouted ! ENDIF DUP EXECUTE verify SWAP 1- DUP 0= IF DROP TRUE ELSE SWAP FALSE ENDIF UNTIL empty? IF from here move here h3 = IF current-player White = IF COMPILE WhitePieces++ ELSE COMPILE BlackPieces++ ENDIF capture ENDIF isPromouted @ IF current-piece-type 1+ change-type ENDIF is-rosette? IF q1 piece-type-at q5 create-piece-type-at ELSE q5 capture-at ENDIF add-move ENDIF ENDIF ; : OnNewGame ( -- ) RANDOMIZE ; : OnIsGameOver ( -- gameResult ) repetition-reset #UnknownScore current-player White = IF BlackPieces @ 7 - 0= IF DROP #LossScore ENDIF ENDIF current-player Black = IF WhitePieces @ 7 - 0= IF DROP #LossScore ENDIF ENDIF ;
ご注意
オンボード変数の使用については、Axiomドキュメントのセクション3.9.4「ボード変数の更新」で説明しています。
完全なゲームを取得するには、フィギュアの戦いと特別なフィールドの処理を実装する必要があります。 これらの詳細は基本的に新しいものを何も載せていないので、これらの詳細で記事を散らかしません。 興味のある方は、 GitHubで「Royal Game of Ur」の完全な実装を確認できます 。
基本的な本能
ZoGの主なハイライトは、その汎用性です。 ZRFでは、ルールを宣言するだけで、新しいゲームを作成(または既存のゲームを記述)できます。 はい、それは特殊なプログラムよりも著しく悪いですが、ほとんどすべてのゲームのプロトタイプをすばやく作成するこのような機会は価値があります! ZoG用に開発されたアプリケーションの数は 、それ自体を物語っています。
公理も普遍的です。 ZoGの不愉快な制限の多くを取り除き、ZoGが対応していないボードゲームを記述することができます。 ブールフラグを操作する代わりに本格的な算術演算を使用する1つの可能性は、この製品を質的に高いレベルに引き上げますが、これはAxiomの主な利点ではありません! ZoGのプレイは良くも悪くもありますが、私たちにとってAIはブラックボックスです。 彼のゲームの品質に影響を与えることはできません! Axiomは、最適な動きを選択するためのアルゴリズムの開発に参加する機会を提供します(ただし、必須ではありません)。
AI Axiomの作業を妨げる最も明白な可能性は、各位置を評価するための重み関数の選択です。 私たちに必要なのは、 OnEvaluateを再定義することだけです。 チップの最初から最後までの全体的なプロモーションを基礎として、非常に単純な評価関数を作成してみましょう。 開始位置でのチップの配置を重み0で評価し、フルパスを通過したチップは、たとえば100などのより大きな数で評価されます。前進)。 もちろん、敵については、反対の符号で取得した同じ推定値を使用します。 敵の位置が良いほど、位置が悪くなります。
簡易評価機能
VARIABLE whiteScored VARIABLE blackScored : Score ( value piece-type player pos -- score ) DUP not-empty-at? IF DUP player-at White = IF whiteScored -- ELSE blackScored -- ENDIF DUP ROT SWAP player-at = ROT ROT piece-type-at = AND NOT IF DROP 0 ENDIF ELSE DROP DROP DROP DROP 0 ENDIF ; : OnEvaluate ( -- score ) 7 whiteScored ! 7 blackScored ! 0 1 White i1 Score 0 1 White j1 Score + 0 1 White k1 Score + 0 1 White l1 Score + 0 1 White m1 Score + 0 1 White n1 Score + 0 1 White o1 Score + 0 1 Black i5 Score + 0 1 Black j5 Score + 0 1 Black k5 Score + 0 1 Black l5 Score + 0 1 Black m5 Score + 0 1 Black n5 Score + 0 1 Black o5 Score + 1 1 White l2 Score + -1 1 Black l4 Score + 2 1 White k2 Score + -2 1 Black k4 Score + 3 1 White j2 Score + -3 1 Black j4 Score + 4 1 White i2 Score + -4 1 Black i4 Score + 5 1 White i3 Score + -5 1 Black i3 Score + 6 1 White j3 Score + -6 1 Black j3 Score + 7 1 White k3 Score + -7 1 Black k3 Score + 8 1 White l3 Score + -8 1 Black l3 Score + 9 1 White m3 Score + -9 1 Black m3 Score + 10 1 White n3 Score + -10 1 Black n3 Score + 11 1 White o3 Score + -11 1 Black o3 Score + 12 1 White o2 Score + -12 1 Black o4 Score + 13 1 White p2 Score + -13 1 Black p4 Score + 14 2 White p3 Score + -14 2 Black p3 Score + 15 2 White p4 Score + -15 2 Black p2 Score + 16 2 White o4 Score + -16 2 Black o2 Score + 17 2 White o3 Score + -17 2 Black o3 Score + 18 2 White n3 Score + -18 2 Black n3 Score + 19 2 White m3 Score + -19 2 Black m3 Score + 20 2 White l3 Score + -20 2 Black l3 Score + 21 2 White k3 Score + -21 2 Black k3 Score + 22 2 White j3 Score + -22 2 Black j3 Score + 23 2 White i3 Score + -23 2 Black i3 Score + 1 1 White c2 Score + 1 1 White c3 Score + 1 1 White c4 Score + -1 1 Black d2 Score + -1 1 Black d3 Score + -1 1 Black d4 Score + 3 1 White a2 Score + 3 1 White a3 Score + 3 1 White a4 Score + -3 1 Black b2 Score + -3 1 Black b3 Score + -3 1 Black b4 Score + 7 1 White f2 Score + 7 1 White f3 Score + 7 1 White f4 Score + -7 1 Black f2 Score + -7 1 Black f3 Score + -7 1 Black f4 Score + 10 1 White g2 Score + 10 1 White g3 Score + 10 1 White g4 Score + -10 1 Black g2 Score + -10 1 Black g3 Score + -10 1 Black g4 Score + 11 1 White e2 Score + 11 1 White e3 Score + 11 1 White e4 Score + -11 1 Black e2 Score + -11 1 Black e3 Score + -11 1 Black e4 Score + 17 2 White e2 Score + 17 2 White e3 Score + 17 2 White e4 Score + -17 2 Black e2 Score + -17 2 Black e3 Score + -17 2 Black e4 Score + 18 2 White g2 Score + 18 2 White g3 Score + 18 2 White g4 Score + -18 2 Black g2 Score + -18 2 Black g3 Score + -18 2 Black g4 Score + 21 2 White f2 Score + 21 2 White f3 Score + 21 2 White f4 Score + -21 2 Black f2 Score + -21 2 Black f3 Score + -21 2 Black f4 Score + whiteScored @ 100 * + blackScored @ 100 * - current-player Black = IF NEGATE ENDIF ;
, Axiom . , . , ( ), , , :
: Mobility ( -- mobilityScore ) move-count \ Number of moves available to us. current-player TRUE 0 $GenerateMoves \ Generate moves for opponent move-count \ Number of moves available to opponent. - \ #friendlyMoves - #unfriendlyMoves $DeallocateMoves \ Deallocate the opponent's move list ; : OnEvaluate ( -- score ) Mobility current-player material-balance 3 * + ;
move-count , material-balance , , {value} ( , «»).
, , ? , , , , . , « », « »! Axiom :
VARIABLE BestScore \ Keep track of the best score found so far by our search engine. VARIABLE Nodes \ The number of possibilities explored by our search engine. VARIABLE Eated VARIABLE Rosettes : enemy-value-at ( pos -- value ) DUP empty-at? IF DROP 0 ELSE 0 SWAP player-at current-player <> IF DROP 1 ENDIF ENDIF ; : friend-value-at ( pos -- value ) DUP empty-at? IF DROP 0 ELSE 1 SWAP player-at current-player <> IF DROP 0 ENDIF ENDIF ; : Make_enemy_p ( pos -- ) <BUILDS , DOES> @ enemy-value-at ; : Make_friend_p ( pos -- ) <BUILDS , DOES> @ enemy-value-at ; i1 Make_enemy_p e0 j1 Make_enemy_p e1 k1 Make_enemy_p e2 l1 Make_enemy_p e3 m1 Make_enemy_p e4 n1 Make_enemy_p e5 o1 Make_enemy_p e6 i5 Make_enemy_p e7 j5 Make_enemy_p e8 k5 Make_enemy_p e9 l5 Make_enemy_p e10 m5 Make_enemy_p e11 n5 Make_enemy_p e12 o5 Make_enemy_p e13 i2 Make_friend_p r0 i4 Make_friend_p r1 l3 Make_friend_p r2 o2 Make_friend_p r3 o4 Make_friend_p r4 : CountEated ( -- count ) e0 e1 + e2 + e3 + e4 + e5 + e6 + e7 + e8 + e9 + e10 + e11 + e12 + e13 + ; : CountRosettes ( -- count ) r0 r1 + r2 + r3 + r4 + ; : Score ( -- score ) Eated @ CountEated < IF 10 ELSE 0 ENDIF Rosettes @ CountRosettes < IF 5 ELSE 0 ENDIF + ; : Custom-Engine ( -- ) -1000 BestScore ! \ Keep track of the best score. 0 Nodes ! \ Count the number of possibilities explored. CountEated Eated ! CountRosettes Rosettes ! ( Notes: 1 - We do not need to invoke $GenerateMoves since they have already been generated for the current player { since ZoG has called DLL_GenerateMoves prior to calling DLL_Search}. 2 - ZoG does not invoke the search engine if there are no moves, so we can safely assume. that at least one move exists. Thus we can use BEGIN..UNTIL instead of BEGIN...WHILE..REPEAT for iterating moves. ) $FirstMove \ Obtain the address of the first move. BEGIN $CloneBoard \ Create a temporary copy of the current board. DUP $MoveString CurrentMove! \ Inform ZoG of the current move being examined. DUP .moveCFA EXECUTE \ Apply the move to the board by executing its code. Score \ Calculate the score for the new board. BestScore @ OVER < \ Have we found a better score? IF DUP BestScore ! \ Save the improved score. Score! \ Inform ZoG of the improved score. DUP $MoveString BestMove! ELSE DROP \ We didn't find a better move, drop the score. ENDIF $DeallocateBoard \ Done with the revised board. Nodes ++ \ Count one more node explored. Nodes @ Nodes! \ Inform ZoG of the node count. $Yield \ Allow ZoG to dispatch Windows messages. $NextMove \ Advance to the next move. DUP NOT \ No more moves? UNTIL DROP ; {players {player} White {search-engine} Custom-Engine {player} Black {search-engine} Custom-Engine {player} ?Dice {random} players}
. , , . , , OnEvaluate , . . «», , , .
, Axiom {first} {random} . axiom.4th:
: $RandomMoveEngine $FirstMove 0 $movesList @ CELLSIZE + @ 1- $RAND-WITHIN BEGIN DUP 0> WHILE SWAP @ SWAP $Yield 1- REPEAT DROP ( move ) $MoveString DUP CurrentMove! BestMove! 1 Nodes! 0 Score! 0 Depth! ; : {random} ['] $RandomMoveEngine $CompileEngine ; : $FirstMoveEngine $FirstMove $MoveString DUP CurrentMove! BestMove! $Yield ; : {first} ['] $FirstMoveEngine $CompileEngine ;
先ほど言ったように、オープンソースの(一部でも)ソースコードは素晴らしいです!
嘘、露骨な嘘と統計
さて、新しいゲームを作成し、ZoGを使用してプレイできます。さまざまな移動選択アルゴリズムを備えたいくつかのゲームオプションを実装しましたが、どれがより良いかをどのように判断するのですか もちろん、ダースの「専門家」を集めて、それぞれのオプションで100回プレイするように依頼することができます。私の友人が言ったように、「それは何年も続くことができます。」もっと良い方法があります!
Axiomは、テストプロセスを自動化するAutoPlayユーティリティを提供します。自動化のパスをたどる最初のことは、ゲームオプションを作成することです。
(variant (title "Ur [random]")) (variant (title "Ur [simple evaluation]")) (variant (title "Ur [aggressive]"))
これらの行をZRFファイルの最後に追加した後、ZRF Converterを再度起動して、ゲームの4番目のバージョンを取得します。これらのファイルを変更して、プログラムで使用される戦略に影響を与える必要があります。ここでは、たとえば、最も単純なオプションの1つに見えます。
LOAD Ur.4th ( Load the base Ur game ) {players {player} White {random} {player} Black {random} {player} ?Dice {random} players}
見やすいように、説明の個々のセクションを再定義して、すべての共有コードをロードされたスクリプトファイルに取り込むことができます。
オプションが作成された後、あるオプションのゲームモードで別のオプションに対してゲームを開始できます。これが自動再生の主な利点です!プレイヤーがさまざまな戦略を使用してプレイするオプションを作成する必要はありません。次のコマンドを入力するだけで十分です。
AutoPlay Ur-[random] Ur-[random] 100
. ( AutoPlay ) . . , ZoG! , ZSG-. , , , , , ( , «»):
Final results: Player 1 "Ur-[random]", wins = 52. Player 2 "Ur-[random]", wins = 48. Draws = 0 100 game(s) played
ZSG- , , ZoG . , ( , ).
ZSG-, , , , , / . , , «» :
#!/usr/bin/perl -w my @S = (0, 0, 0, 0, 0, 0); my $ix = 0; my $T; while (<>) { if (/results/) { my $d = $S[0] - $S[1]; print "$T, $d, $S[3], $S[2], $S[4], $S[5]\n"; @S = (0, 0, 0, 0, 0, 0); $ix = 0; } else { if (/^(\d+)\.\s+[^?].*$/) { $T = $1; if (/x h3/) { $S[$ix]++; } if (/Pass|^(\d+)\.\s+x\s+q5\s*$/) { $S[$ix + 2]++; } if (/Black init [ijklmno]5/) { $S[4]++; } if (/White init [ijklmno]1/) { $S[5]++; } $ix++; if ($ix > 1) { $ix = 0; } } } }
これで、開発したオプションのゲーム品質を比較するために必要なすべてが揃いました。次の3つのオプションを検討します。
- 移動のランダムな選択(ランダム)
- 単純な評価関数(simple)
- 「積極的な」選択アルゴリズムストロークに(積極的な)
ランダムvsランダム
( , , 150 ):

, ( — ):
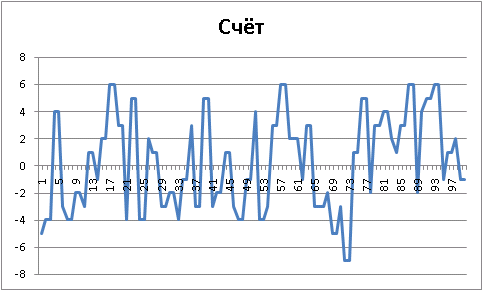
«» :

, , , :

, ( — ):

«» :

, , , :
Final results: Player 1 "Ur-[random]", wins = 52. Player 2 "Ur-[random]", wins = 48. Draws = 0 100 game(s) played
ランダムvsシンプル
:
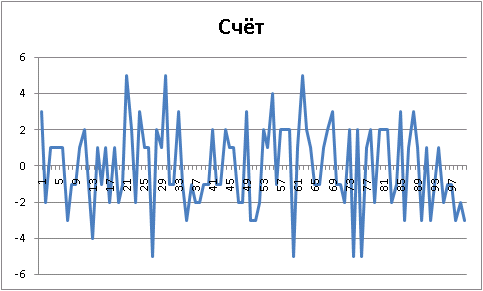
:

:
Final results: Player 1 "Ur-[random]", wins = 50. Player 2 "Ur-[simple-evaluation]", wins = 50. Draws = 0 100 game(s) played
単純対ランダム
:
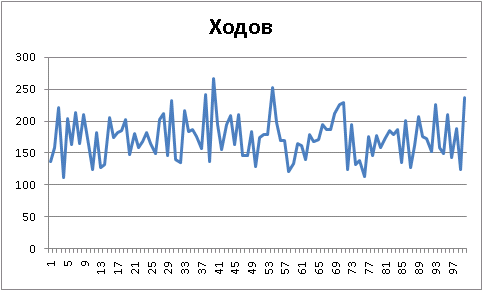
«» :
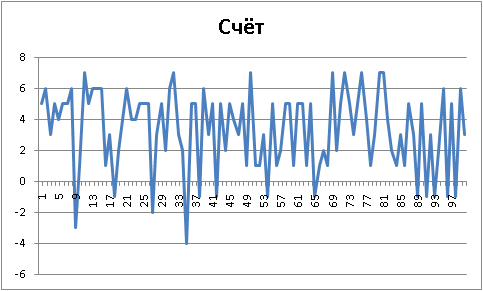

«» :

Final results: Player 1 "Ur-[simple-evaluation]", wins = 87. Player 2 "Ur-[random]", wins = 13. Draws = 0 100 game(s) played
ランダムvsアグレッシブ
:
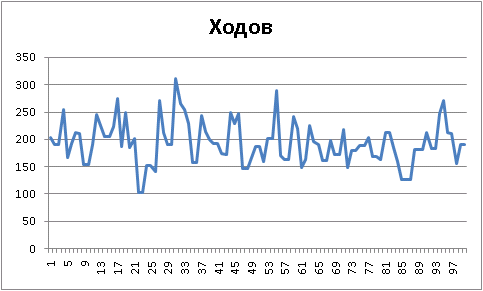
random ( ):

, , «» :
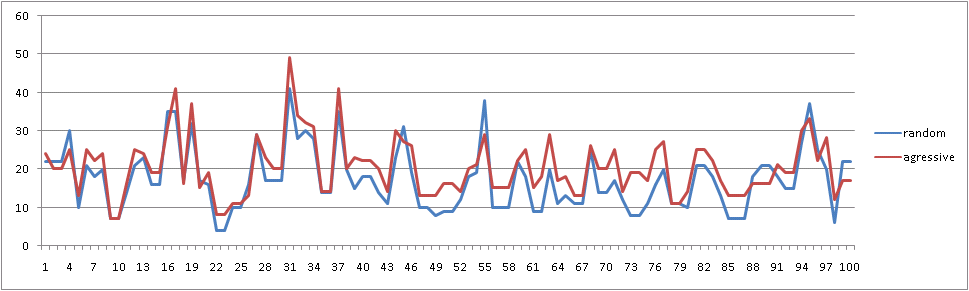
«» , !

random ( ):

, , «» :

«» , !
Final results: Player 1 "Ur-[random]", wins = 25. Player 2 "Ur-[aggressive]", wins = 75. Draws = 0 100 game(s) played
アグレッシブvsランダム
:

«» «» !
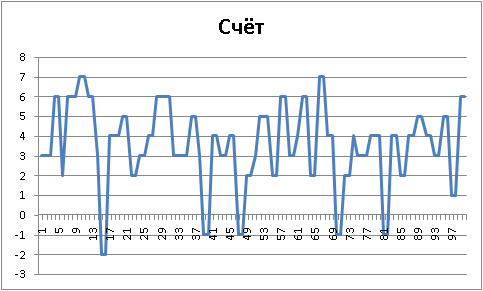
, «» , :
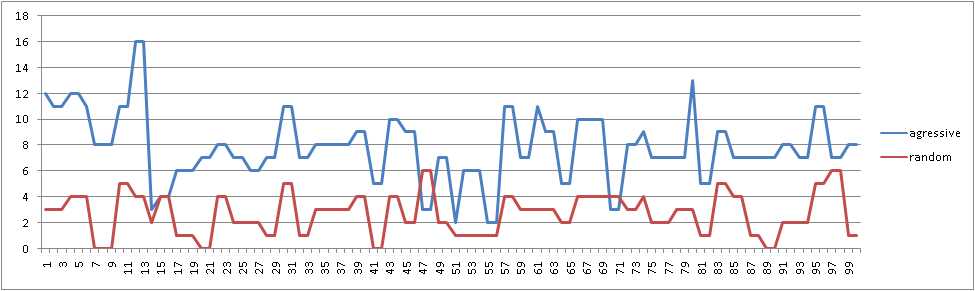

«» «» !

, «» , :

Final results: Player 1 "Ur-[aggressive]", wins = 90. Player 2 "Ur-[random]", wins = 10. Draws = 0 100 game(s) played
シンプルvsアグレッシブ
, . , simple :
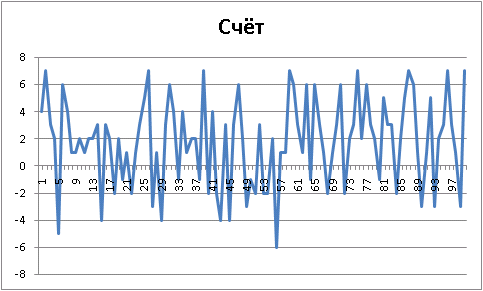
!
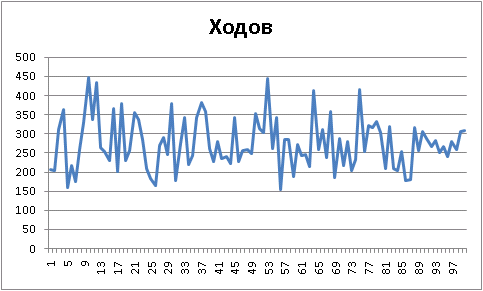

!

Final results: Player 1 "Ur-[simple-evaluation]", wins = 73. Player 2 "Ur-[aggressive]", wins = 27. Draws = 0 100 game(s) played
アグレッシブvsシンプル
, agressive :

«» , , «»:
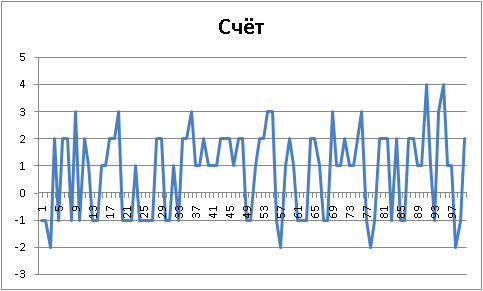

«» , , «»:

Final results: Player 1 "Ur-[aggressive]", wins = 64. Player 2 "Ur-[simple-evaluation]", wins = 36. Draws = 0 100 game(s) played
ところで、次のすばらしい行に注意してください。
Draws = 0
, Axiom «3-Time Repetition Draw!». . , ZoG . (3-4 ) . « », , , ZoG ( Axiom) ! AutoPlay, . , , ZoG, .
… !
もちろん、たった1つの記事では、Axiom Development Kitのような複雑で多面的な製品についてすべてを伝えることは不可能です。開発者によって発表された機能を参照してください。
公理エンジンの機能
- Contains a universal game engine designed to play a large variety of games. The search engine is not optimized for any particular class of games.
- Allows (actually requires) the game programmer to specify a custom game AI. This is one of the main benefits of Axiom. Some 'built-in' AI helpers are provided. For example, one helper is simply the difference between the number of available moves for each player, another takes into consideration material advantage. The list is expected to grow over time.
- «Minimax with Alpha-Beta pruning» search algorithm.
- Iterative deepening with transposition table.
- Zobrist hashing
- Limited move reordering based on 'best move from previous iteration' stored in the transposition table.
- Full width searching.
- Support for 'partial' and 'pass' moves.
- Supports 'teams'.
- Time management.
- Supports additional user-supplied custom engines.
- Programmer controlled quiescence (currently experimental)
, , ZoG. Axiom (Ring Buffer) «» « ». , ( ZoG, , ), Axiom , .
. , . , ZoG 60 , Axiom, .