この記事では、音声認識などのソフトウェア開発の興味深い分野の基本について考えたいと思います。 当然、私はこのトピックの専門家ではないので、私の話には不正確、エラー、失望がたくさんあります。 しかし、私の「仕事」の主な目標は、その名前が示すように、問題の専門的な分析ではなく、基本概念、問題、およびそれらの解決策の説明です。 一般に、私は猫の下で歓迎されているすべての人に尋ねます！
プロローグ
そもそも、音声は一連の音です。 音は、さまざまな周波数の音の振動（波）の重ね合わせ（重ね合わせ）です。 物理学からわかるように、波は振幅と周波数という2つの属性によって特徴付けられます。
オーディオ信号をデジタルメディアに保存するには、それを多くのギャップに分割し、それぞれの「平均」値をとる必要があります。
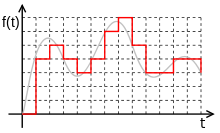
このようにして、機械的振動は、最新のコンピューターでの処理に適した一連の数値に変わります。
したがって、音声認識のタスクは、数値セット（デジタル信号）と辞書（ロシア語など）からの単語の「マッチング」に限定されます。
実際、このまさに「比較」を実現する方法を見てみましょう。
入力データ
オーディオデータを含むファイル/ストリームがあるとします。 まず、それがどのように機能し、どのように読むかを理解する必要があります。 最も簡単なオプション-WAVファイルを見てみましょう。
この形式は、ファイル内に2つのブロックが存在することを意味します。 最初のブロックは、オーディオストリームに関する情報を含むヘッダーです：ビットレート、周波数、チャンネル数、ファイル長など。 2番目のブロックは、「生の」データ、つまり同じデジタル信号、振幅のセットで構成されています。
この場合のデータ読み取りのロジックは非常に単純です。 ヘッダーを読み取り、いくつかの制限（圧縮の欠如など）を確認し、特別に割り当てられた配列にデータを保存します。
例 。
認識
純粋に理論的には、既存のサンプルを（要素ごとに）他のサンプルと比較できます。テキストはすでにわかっています。 つまり、スピーチを「認識」しようとします...しかし、これをしない方が良いです:)
私たちのアプローチは、音声の音色（単語を発音する人）、ラウドネス、発音速度の変化に対して安定している必要があります（少なくとも少し）。 2つのオーディオ信号の要素ごとの比較では、もちろんこれは達成できません。
したがって、少し異なる方法で進みます。
フレーム
まず、データを小さな時間枠（フレーム）に分割します。 さらに、フレームは厳密に次々に移動するのではなく、「オーバーラップ」する必要があります。 つまり 1つのフレームの終わりが別のフレームの始まりと交差する必要があります。
特定のポイントよりも特定の間隔で波を分析する方がはるかに便利なので、フレームは特定の信号値よりもデータ分析の適切な単位です。 重複するフレームの位置により、フレームの分析結果を平滑化し、フレームの概念を元の関数（信号値）に沿って移動する特定の「ウィンドウ」に変えることができます。
最適なフレーム長は10ミリ秒のギャップ、つまり「オーバーラップ」-50％に対応する必要があることが実験的に確立されました。 （少なくとも私の実験では）平均ワード長が500msであるとすると、このステップでは約500 /（10 * 0.5）=ワードあたり100フレームが得られます。
単語分割
音声認識で解決しなければならない最初のタスクは、この音声を個別の単語に分割することです。 簡単にするために、この場合、音声にはいくつかの一時停止（沈黙の間隔）が含まれていると仮定します。これは単語の「区切り文字」と見なすことができます。
この場合、いくつかの値、しきい値-上の値は単語、下の値-沈黙を見つける必要があります。 いくつかのオプションがあります。
- 定数によって設定されます（元の信号が常に同じ条件で同じ方法で生成される場合に機能します）。
- 信号値をクラスター化し、無音に対応する一連の値を明確に強調します（無音が元の信号の大部分を占める場合にのみ機能します）。
- エントロピーを分析します。
ご想像のとおり、ここで最後の点について説明します:)そもそも、エントロピーは無秩序の尺度であり、「あらゆる経験の不確実性の尺度」です（c）。 この場合、エントロピーとは、特定のフレーム内で信号がどれだけ「変動」するかを意味します。
特定のフレームのエントロピーを計算するには、次の手順を実行します。
- 信号が正規化され、その値がすべて[-1; 1]の範囲にあるとします。
- フレーム信号値のヒストグラム（分布密度）を作成します。
エントロピーを次のように計算します
;
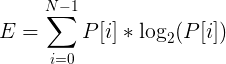例 。
そして、エントロピーの価値を得ました。 しかし、これはフレームのもう1つの特徴であり、音と静寂を分離するために、それを何かと比較する必要があります。 一部の記事では、（すべてのフレーム間で）最大値と最小値の間の平均に等しいエントロピーしきい値を取ることを推奨しています。 しかし、私の場合、このアプローチでは良い結果が得られませんでした。
幸いなことに、エントロピーは（値の同じ平均二乗とは対照的に）比較的独立した値です。 これにより、定数（0.1）の形式でしきい値の値を選択できました。
それでも、問題はそこで終わるわけではありません：（エントロピーは単語の途中で（母音で）垂れ下がることがあります。または、わずかなノイズにより突然跳ね上がることがあります。最初の問題に対処するために、 2番目の問題は、「最小語長」を使用して、選択に合格していない（最初の段落で使用されていない）すべての候補をカットすることで解決されます。
原則として、音声が「明瞭」でない場合、フレームの初期セットを特定の方法で準備されたサブシーケンスに分割して、それぞれが認識手順の対象となるようにすることができます。 しかし、これは完全に異なる話です:)
Mfcc
したがって、特定の単語に対応するフレームのセットがあります。 最小抵抗の経路をたどり、そのすべての値の平均二乗（ルート平均二乗）をフレームの数値特性として使用できます。 ただし、このようなメトリックには、さらなる分析に適した情報がほとんど含まれていません。
これは、メル周波数ケプストラル係数が作用する場所です。 ウィキペディア（ご存知のとおり、嘘ではない）によると、MFCCは信号スペクトルのエネルギーの一種の表現です。 その使用の利点は次のとおりです。
- 信号スペクトル（つまり、直交[co]正弦関数の基底に沿った展開）が使用されます。これにより、さらなる分析中に信号の波の「性質」を考慮することができます。
- スペクトルは特別なメルスケールに投影され、人間の知覚にとって最も重要な周波数を抽出することができます。
- 計算される係数の数は、任意の値（12など）で制限できます。これにより、フレームを圧縮し、その結果、処理される情報の量を制限できます。
特定のフレームのMFCC係数を計算するプロセスを見てみましょう。
フレームをベクトルとして想像してください
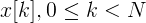Nはフレームサイズです。
フーリエ展開
まず、離散フーリエ変換を使用して信号スペクトルを計算します（「高速」FFT実装が望ましい）。
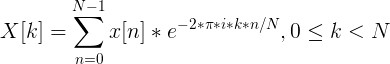
フレームの境界の値を「滑らかにする」ために、取得した値にハミングウィンドウ関数を適用することもお勧めします。
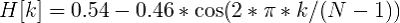
つまり、結果は次の形式のベクトルになります。
X軸に沿ったこの変換後、信号の周波数（hz）が得られ、Y軸に沿って（複素数値から抜け出す方法として）振幅があることを理解することが重要です。
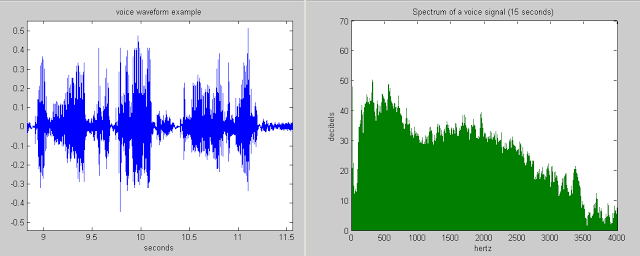
メルフィルターの計算
メルとは何かから始めましょう。 繰り返しになりますが、Wikipediaによると、melは平均的な人々の主観的な認識に基づく「ピッチの心理物理学的単位」です。 主に音の周波数に依存します（音量と音色にも依存します）。 言い換えれば、この値は、特定の周波数の音が私たちにとって「重要」であることを示しています。
周波数は、次の式を使用してチョークに変換できます（「式1」として覚えておいてください）。
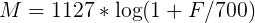
逆変換は次のようになります（「式2」として覚えておいてください）。
メル/周波数プロット：
しかし、タスクに戻ります。 256要素のサイズのフレームがあるとしましょう。 （オーディオ形式のデータから）このフレームのサウンド周波数は16000hzであることがわかります。 人間の発話が[300; 8000] hz。 希望するチョーク係数の数は、M = 10（推奨値）に設定されています。
上記で得られたスペクトルをメルスケールで分解するには、フィルターの「櫛」を作成する必要があります。 実際、各メルフィルターは三角窓関数です 。これにより、特定の周波数範囲でエネルギー量を合計し、メル係数を取得できます。 チョーク係数の数と分析された周波数範囲がわかれば、このようなフィルターのセットを作成できます。
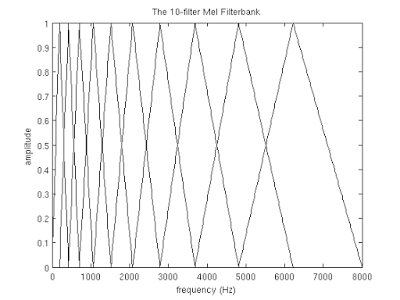
チョークファクターの数が多いほど、フィルターのベースが広くなることに注意してください。 これは、対象の周波数範囲がフィルターで処理される範囲にチョークスケールで分割されるためです。
しかし、再び気が散りました。 したがって、私たちの場合、対象となる周波数の範囲は[300、8000]です。 式1によれば、チョークスケールでは、この範囲は[401.25; 2834.99]。
さらに、10個の三角フィルターを作成するには、12個の参照ポイントが必要です。
m [i] = [401.25、622.50、843.75、1065.00、1286.25、1507.50、1728.74、1949.99、2171.24、2392.49、2613.74、2834.99]
チョークスケールでは、ポイントは等間隔になっていることに注意してください。 式2を使用してスケールをヘルツに変換します。
h [i] = [300、517.33、781.90、1103.97、1496.04、1973.32、2554.33、3261.62、4122.63、5170.76、6446.70、8000]
ご覧のとおり、スケールは徐々に拡大し始め、それにより低および高周波数での「重要性」の成長のダイナミクスが平準化されました。
次に、結果のスケールをフレームのスペクトルに重ね合わせる必要があります。 覚えているように、X軸に沿って周波数があります。 スペクトルの長さは256要素ですが、16000hzに収まります。 単純な割合を解くと、次の式を取得できます。
f（i）= floor（（frameSize + 1）* h（i）/ sampleRate）
私たちの場合、これは同等です
f（i）= 4、8、12、17、23、31、40、52、66、82、103、128
以上です！ スペクトルのX軸上の基準点がわかっているので、次の式を使用して必要なフィルターを簡単に構築できます。
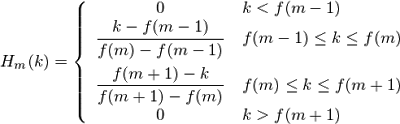
フィルターの適用、スペクトルエネルギーの対数
フィルターの使用は、その値とスペクトルの値のペアワイズ乗算です。 この操作の結果がメル係数です。 M個のフィルターがあるため、係数の数は多くなります。
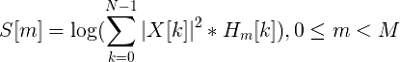
ただし、メルフィルターはスペクトル値ではなくエネルギーに適用する必要があります。 次に、結果を前置します。 このようにして、ノイズに対する係数の感度が低下すると考えられています。
コサイン変換
離散コサイン変換（DCT）は、同じ「ケプストラム」係数を取得するために使用されます。 その意味は、得られた結果を「絞る」ことで、最初の係数の重要性を高め、後者の重要性を減らします。
この場合、DCTIIは次の乗算なしで使用されます。
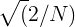（スケール係数）。
これで、各フレームについて、さらに分析するために使用できるM mfcc係数のセットができました。
アップストリームメソッドのサンプルコードはこちらにあります 。
認識アルゴリズム
ここで、親愛なる読者、主な失望があなたを待っています。 インターネット上で、どの認識方法が優れているかについて、非常に知的な（そしてそうではない）紛争が多く発生しました。 隠れマルコフモデルを支持する人、ニューラルネットワークを支持する人、誰かの考えは原則として理解できない:)
いずれにせよ、多くの設定がSMMに正確に与えられており、将来的にはコードに追加するつもりです... :)
現時点では、はるかに効果的ではないが、時にはより簡単な方法で停止することを提案しています。
そして、私たちの仕事は辞書から単語を認識することであることを忘れないでください。 簡単にするために、最初の10桁の名前を認識します：「one」、「two」、「three」、「four」、「five」、「six」、「seven」、「eight」、「nine」、「ten」。
それでは、iPhone / Androidを手に取り、Lの同僚を調べて、これらの単語を記録のために口述するように依頼してみましょう。 次に、（いくつかのローカルデータベースまたは単純なファイルで）各単語Lを対応するレコードのmfcc係数のセットに関連付けます。
この通信を「モデル」と呼び、プロセス自体を機械学習と呼びます。 実際、データベースへの新しいサンプルの単純な追加は、機械学習との非常に弱いつながりを持っています...しかし、ファッショナブルという用語はとても痛いです:)
これで、特定のmfcc係数のセット（認識可能な単語）に対して「最も近い」モデルを選択することになりました。 一見すると、問題は非常に簡単に解決できます。
- 各モデルについて、識別されたmfccベクトルとモデルベクトル間の平均（ユークリッド）距離を見つけます。
- 真であるモデル、最小距離までの平均距離を選択します。
ただし、Andrei Malakhovと彼のエストニア語の一部の両方で同じ単語を発音できます。 言い換えれば、同じ単語のmfccベクトルのサイズは異なる場合があります。
幸いなことに、異なる長さのシーケンスを比較するタスクは、動的タイムワーピングアルゴリズムの形ですでに解決されています。 この動的プログラミングアルゴリズムは、ブルジョアWikiと正統派ハブレの両方で美しく描かれています。
行う価値のある唯一の変更は、距離を見つける方法です。 モデルのmfccベクトルは、実際にはフレームから取得した次元Mのmfcc「サブベクトル」のシーケンスであることを覚えておく必要があります。 したがって、DTWアルゴリズムは、次元Mのこれらの同じ「サブベクトル」のシーケンス間の距離を見つける必要があります。つまり、フレームのmfcc「サブベクトル」間の距離（ユークリッド）が距離行列の値として使用されます。
例 。
実験
大規模な「トレーニング」サンプルでこのアプローチの作業をテストする機会がありませんでした。 非合成条件下で各単語の3つのコピーのサンプルのテスト結果は、穏やかに言えば、最良の結果-正しい認識の65％を示しました。
それにもかかわらず、私のタスクは、音声認識のための最大のシンプルなアプリケーションを作成することでした。 「概念実証」と言うには:)
実装
気配りのある読者は、記事にGitHubプロジェクトへの多くのリンクが含まれていることに気付きました。 これは大学以来の私の最初のC ++プロジェクトであることは注目に値します。 これは、同じ大学以来、算術平均よりも複雑なものを計算するための私の最初の試みでもあります...言い換えれば、それは絶対に保証なしで来ます（c）:)