1つの組み合わせ生成アルゴリズム

高校の組み合わせ論は、原則として、組み合わせ、順列、または配置の数について、3つのよく知られた式のいずれかを適用する必要があるテキストの問題に限定されます。 離散数学のインスティテュートコースでは、ブラケットシーケンス、ツリー、グラフなどのより複雑な組み合わせオブジェクトについても話します...さらに、原則として、特定のパラメーターnの特定のタイプのオブジェクト数、たとえばn頂点のツリー数を計算するタスクを設定します。 固定nのオブジェクトの数を学習した後、より複雑な質問をすることもできます。これらすべてのオブジェクトを妥当な時間で表示する方法は？ この種の問題を解決するアルゴリズムは、組み合わせ生成アルゴリズムと呼ばれます。 たとえば、このようなアルゴリズムは、ドナルドクヌースによる「プログラミングの芸術」第4巻の第1章の主題です。 Knutは、すべてのタプル、数値のパーティション、ツリー、およびその他の構造を生成するアルゴリズムを詳細に検討します。 適度に高速に動作するある種のアルゴリズムを考え出すことは、これらのタスクのそれぞれにとって難しいことではありませんが、さらなる最適化では深刻な問題が発生する可能性があります。



アカデミック大学で擁護された修士論文を書く過程で、特別なクラスの問題に適した組み合わせ生成のアルゴリズムの1つを研究して適用する必要がありました。 これは、いくつかの等価関係が追加で導入される構造の生成です。 危機にwhatしているものを明確にするために、簡単な例を挙げます。 六角形のすべての三角形分割を生成してみましょう。 次のようなものが得られます。











そのようなすべての三角形分割を返すアルゴリズムを書くのは非常に簡単です。 たとえば、この手順は機能します。いくつかのエッジを修正し（エッジ1〜6にします）、その後、サイクルでは、その端ではない頂点をソートします。 現在の頂点と固定エッジで三角形を作成し、残りの2つの領域を再帰的に三角形分割します。 このアルゴリズムの操作から生じる三角形分割をよく見ると、それらの多くがほぼ同じであり、頂点のラベル（数値）の配置方法のみが異なることに気付くでしょう。 そのため、次の図に示すように、いわゆるラベルなしの三角形分割を生成するアルゴリズムを考え出すと便利です。













より形式的には、オブジェクトのセットに等価なセットを作用させ、セット全体を互いに同形のオブジェクトのクラスに分割します。 各クラスから1つの代表を生成する必要があります。 おそらく、2番目の図の2つの右側の三角形分割も互いに非常に似ており、そのうちの1つだけを残すことができることに気づいたでしょう。 現実には、それは私たちがどの種類の同値関係を選んだかに依存します。 回転後に互いに重ね合わせることができる三角形のみを同型と見なす場合、それらは4つあり、六角形を再度回転する可能性を許可する場合は3つです。



各クラスから1つの代表を生成することは難しくないと思われます。すべてのオブジェクトを生成した後、ペアで同型をテストし、重複をスローします。 残念ながら、オブジェクトの種類によっては、nが小さい場合でもひどく長く動作します。 たとえば、2つのグラフの同型をチェックする問題は、多項式時間では解決できません。つまり、この問題をできるだけ解決しないサブルーチンを呼び出すことをお勧めします。 提案された単純なアプローチの別の欠点は、すべてのオブジェクトを同時にメモリに保持する必要があることです。 同時に、正しい答えを与える遅いプログラムを待つ場合、それはまだ理論的には可能ですが、答えの代わりにメモリオーバーフローを取得することはすでに完全に受け入れられません。 そのため、ペアワイズ非同型オブジェクトを生成するには、よりトリッキーな方法を使用する必要があります。 この方法は、多くの特定の組み合わせオブジェクト（グラフ、ツリー、パーティション）について繰り返し再発見され、一般的な用語でIsomorph-Free Exhaustive Generationの記事で説明されました。



この方法については、三角形分割の問題と比較してやや一般的な問題の例として説明します。すべての「解剖」、つまり、ポリゴンを必ずしも三角形に分割するのではなく、入力に供給されるリストの辺の数を持つポリゴンに分割する方法を生成しますプログラム。



この方法を説明するには、いくつかの正式な定義が必要です。



Xを「構造」のセットにします。 セットXの要素は、 ラベル付きオブジェクトと呼ばれます 。 この問題では、マークされたオブジェクトは、頂点に反時計回りに番号が付けられた解剖です。 マークされたセクションのデータ構造は単純です-これらは隣接リストです：

public class Dissection { private int[][] adjacent; ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Gを集合Xに作用する順列グループとします。これは、Xの各ラベル付きオブジェクトxとグループGの各要素gが別のラベル付きオブジェクトy = g * xに関連付けられ、次のプロパティが満たされることを意味します：

1. グループhおよびgの要素の乗算は、オブジェクトxへのアクションの順次適用に対応します：h *（g * x）=（hg）* x。
2. グループeの単位は、マークされた各オブジェクトxをそれ自体に変換します：e * x = x。

セットX全体が相対関係の等価クラスに分割されていることがわかります。x= g * yの場合、xとyは等価です。 三角形分割の最初の例では、グループの要素（0、60、120、180、240、および300度の回転）がセット全体を4つの等価クラスに分割します。これらの要素は、頂点マーキングではなく構造が正確に異なります。 これらの等価クラスは、2番目の図に示されています。 これらのクラスをラベルなしオブジェクトと呼びます 。



Xの各要素に自然数を関連付けます。これを順序と呼びます。 すべての同等のオブジェクトの順序は同じでなければなりません。 このプロパティを使用すると、等価クラス（ラベルなしオブジェクト）の順序を再定義できます。これは、対応するクラスの代表の順序と等しくなります。 図の例では、順序はポリゴン内の頂点の数です。 図内のすべてのラベルなしオブジェクトについては、6です。



これらはかなり一般的な定義でした。 次に、将来のアルゴリズムに固有の定義に移りましょう。 マークされた各オブジェクトxに、2つのセット（ 下位オブジェクトのセットL（x）と上位オブジェクトのセットU（x））を関連付けます 。 これらのセットの要素の順序は、定義によりxの順序と同じです。 下位オブジェクトと上位オブジェクトに正式な要件を与える前に、直感的な説明をしようとします。 下位の各オブジェクトには、現在のオブジェクトから下位のオブジェクトに明確に切り替える方法に関する情報が含まれている必要があります。 たとえば、下部切開オブジェクトは、「極端な」ポリゴンの1つが追加で強調表示されている切開（たとえば、赤く塗られている）であり、この切開から切り取ることができます。 反対に、上位オブジェクトはマークされたオブジェクトと情報であり、明確な方法で「成長」し、順序を増加させることができます。 たとえば、上部解剖は、ポリゴンの側面の1つがさらに強調表示され（たとえば、赤く塗られ）、その上に数字が書き込まれる解剖です。 このような解剖を見ると、新しいポリゴンをどちらの側に貼り付けて順序を増やすかを理解できます。 接着されたポリゴンの辺の数は、エッジに書かれた数によって決まります。 この考えは、同じ解剖に対応する2つのオブジェクト（下と上）を示す次の図で説明できます。











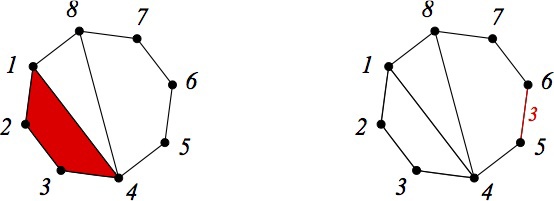
プログラムでは、下部と上部のセクションは次のように表示されます。

 public class LowerDissection { private Dissection dissection; private int after; ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 public class UpperDissection { private Dissection dissection; private int after, size; ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ボトムカットの場合、削除するポリゴンが始まる頂点番号のみを保存します。 上部セクションには、頂点番号が保存されます。その後、新しいポリゴンとその辺の数を接着する必要があります。



一部の下位オブジェクトと上位オブジェクトは「一致」関係にあることがわかります。下位オブジェクトは、下位オブジェクトでエンコードされた方法で順序を減らした後に取得された上位オブジェクトに対応します。











ここでは、下のオブジェクトが上のオブジェクトにマッピングされます。これは、選択した四辺形を削除した結果です。 次の図では、これとは逆になっています。五角形は、上部のオブジェクト、または選択したエッジに5が書き込まれた状態で接着されています。 これにより、操作をロールバックする方法に関する情報を格納する下位オブジェクトが作成されます。











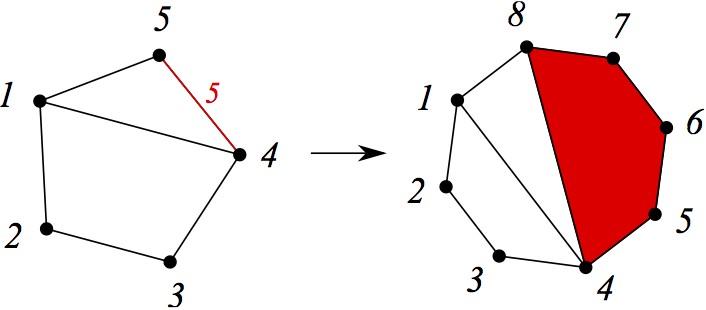
さて、正式には、上記の構造から何が必要か：

1. グループGは、ラベル付き、上部、下部の3種類のオブジェクトに作用します。 これらの3つのセットはそれぞれ、グループのアクションに対して閉じられます（これは、たとえば、グループの要素によって下位オブジェクトに作用した場合、上位オブジェクトを取得することは不可能であることを意味します-むしろ正式な要件です）。
2. マークされた各オブジェクトxとグループgの要素に対して：L（g * x）= g * L（x）; U（g * x）= g * U（x）（g * L（x）という表記は、g * U（x）についても同様に、セットL（x）の各要素にgを適用することを意味します）。
3. 各下位オブジェクトyについて、対応する上位オブジェクトのセットは空ではありません。
4. 下部の2つのオブジェクトyとxが同等（つまり、y = g * x）の場合、それらに対応する上部の2つのオブジェクトも同等です。
5. 上の2つのオブジェクトyとxが同等である場合、それらに対応する2つの下のオブジェクトも同等です。
6. 下位オブジェクトの順序は、対応する上位オブジェクトの順序よりも大きくなります。

この概念をよりよく理解するために、読書から脱線し、セットXとして三角形のないグラフ（つまり、3つの頂点がすべてエッジで同時に接続されていないグラフ）を取得した場合、下部オブジェクトと上部オブジェクトがどのようになるかを考えることをお勧めします）







続けましょう。 ラベルのないオブジェクトから何も噛み付いてはいけません。 したがって、それに対応する（または、マークされたオブジェクトに対応する）下位オブジェクトはありません。 このようなオブジェクトは既約と呼ばれます。 私たちの場合、単一のポリゴンで構成されるカットは既約です。 他のすべては還元可能です。



私たちのアルゴリズムは、すべての非同型カットを、既約カットから始めて、順番を徐々に増やして、順次生成します。 これを行うために、すべての可能な辺からのすべての可能なポリゴンを現在のセクションに固定します。 ただし、問題は、いくつかの方法で同じ解剖に到達できることです。 たとえば、前の2つの写真の下部のオブジェクトに対応する八角形をカットするには、四角形を三角形に接着してから五角形に接着するか、反対に三角形と四角形を五角形に接着することでできます。 したがって、同じ解剖を数回生成することが可能になり、気付くことさえありません。 これはあなたがただ避けたいものです。



新しいカットを生成してこの問題を回避するには、このカットを構築する独自の標準的な方法でポリゴンの最後の追加が正しいかどうかを確認します。 これを行うには、マークされた各オブジェクトに、それが「子孫」である下位オブジェクトのセットを関連付ける関数Pが必要です。 関数Pは、次の要件を満たしている必要があります。

1. L（x）が空の場合、P（x）も空です。
2. L（x）が空でない場合、P（x）は、オブジェクトxに対応するそのような下位オブジェクトのみで構成され、それらのいずれか2つがg * x = xである要素gのアクションの下で相互に変換します。
3. ラベルのないオブジェクトxおよびグループgの要素の場合：g * P（x）= P（g * x）。

2番目の要件に特に注意を払う価値があります。実際、セットP（x）は、オブジェクトxの対称性に関して等価な複数のオブジェクトで構成する必要があることを意味します。 たとえば、カットxが0度と180度の回転に対してのみ対称であるとします。 次に、P（x）は、このようなターンの助けを借りて互いに取得された正確に2つの下位オブジェクトで構成される必要があります。



この例の一般的な要件を満たすようにしましょう。 これを行うには、xの一部を切り取り、その中のマークをn個すべての方法でスクロールします（nは頂点の数です）。 毎回、頂点1と2から「極端な」ポリゴンが始まるとき（切り取られるように）、この番号付けを覚えています。 その後、選択された頂点番号付けのサブ番号付け全体から、隣接関係リストの辞書的に最小限の（他の合理的な順序が適切です）エントリを与えるものを選択します。 これらの番号付けにより、元のオブジェクトx上のいくつかのポリゴンが得られます。対応する番号付けで1と2から始まります。P（x）は、これらのポリゴンが赤で表示されるxの下位オブジェクトで構成されます。 ここでは、写真なしではできません。











そこで、左に示す解剖xを選択し、8つの異なる方法でマークを再配置しました。 メソッドa、c、e、およびgはすぐには適さない：頂点1、2、...、iでは、カット可能なポリゴンが構築されない。 メソッドbとfはメソッドdとhと本質的に同じであることがわかります。 これら4つの方法のうち、ある意味で「最小限」のものを選択します。 すでにお気づきのとおり、必要に応じて最小値を定義することは可能ですが、間違いありません。 たとえば、隣接リストの辞書編集に適した最小限のレコードが適しています。 この場合、メソッドbおよびfが優先されます。 この方法では、元のマークされたオブジェクトx上に三角形2,3,4および6,7,8が得られます。 その結果、右の図に示されている2つの下部オブジェクトが取得されます。



P関数は、高速生成のために最も重要です。 実際、指定された要件を満たし、作業の高速化を維持することは非常に困難です。 ご覧のとおり、ある意味で、関数Pを使用すると、同型まで、どのように極端な多角形を「食い止める」方法が正準であるかを指定できます。 概念が明確であれば、三角形のない既述のグラフに対して関数P（x）がどのように機能するかを考えてみることをお勧めします。







上記のすべての機能を実装する上記のクラスにメソッドを追加するコードは、 リポジトリで最もよく見られます。詳細について説明するには技術的な詳細が多すぎます。



これで、生成アルゴリズムを直接説明する準備がすべて整いました。 削減できない各カットに対して実行されます。 現在の解剖では、すべての非同型の方法で上位オブジェクトを作成し、取得した各上位オブジェクトを順番に増加して下位オブジェクトに拡張します。 次に、P関数を使用して、下位の各オブジェクトをチェックし、実際に対応するマークされたオブジェクトの親であることを確認します。 このチェックに合格した場合、このマークされたオブジェクトは新しい等価クラスの代表であると見なされます。 アルゴリズムを再帰的に実行します。 もちろん、このアルゴリズムの正しさを証明することはできますが、私はすでに形式主義を少しやり過ぎていると感じています。その証拠に対処するために、 元の記事を参照する方が簡単です。



まず、生成を担当するコードを見てみましょう。

 public static void generateSubtreeFrom(Dissection root, int maxOrder) { for (UpperDissection upper : root.createAllUpper()) { LowerDissection lower = upper.createArbitraryLower(); if (lower != null) { Dissection probableChild = lower.getUnderlyingDissection(); if (probableChild.getOrder() <= maxOrder && lower.isParentFor(probableChild)) { root.addChild(probableChild); generateSubtreeFrom(probableChild, maxOrder); } } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして今-すべての非同型カットを最大で8桁までの3.4および5ゴンに生成した結果。 矢印は、親から子孫に向けられています。 すべてのカットは、根が既約オブジェクトであるツリーを形成していることがわかります。









この図面を生成したプログラムのソースコードは、 Googleコードで入手できます 。 彼女の仕事の結果は、graphviz形式の説明です。



結論として、考えられる問題については、原則として、よりシンプルで同時に高速なアルゴリズムを思いつくことができると付け加えます。 ただし、説明されている手順は、誘導的に構築できるほぼすべてのタイプの組み合わせオブジェクトに適用でき、構造を「構築」します。 さらに、アルゴリズムの作成者によれば、少なくとも一部のグラフの種類では、このアプローチにより、今日では最高ではないにしても最高の生成率が得られます。