Clever Geek Handbook

逆運動学：シンプルで高速なアルゴリズム

逆運動学とは何ですか？



インバースキネマティクスのタスクは、与えられたポイントに最もソフトで高速かつ正確な動きを提供するようなジョイント構成のセットを検索することです。 しかし、多くの既存の方法は、計算の複雑さや結果として生じるポーズの不自然さなどの欠点に悩まされています。 この記事では、 Forward and Backward Reaching Inverse Kinematics （以降、単にFABRIK） と呼ばれる新しい（ おそらく2010年執筆時点での ）ヒューリスティック手法について説明します。

FABRIKは、直線上の点を直接取得するために、回転とマトリックスの使用を避けます。 これにより、ビジネスはわずか数回の反復で管理され、計算コストが低く、結果として視覚的に自然なポーズになります。 FABRIKは、いくつかのチェーンやエンドポイントを使用するだけでなく、問題なく制限にも対処します。 この投稿はこの方法に関するものです。





オリジナルは非常に大きく、大量の水、関連する不適切な繰り返しとオフセット、および他のアルゴリズムとの比較があるため、このスクイーズを理解してください。 それにもかかわらず、私はこれを無視することにしたので、それはテキストのほんの一部しか含んでいないが、それは本質を反映している。 perev。



1.人工体モデル

多くのソリッドのシステムは、エッジで接続されたノードと呼ばれるソリッドのセットで構成されています。 すべてのエッジはモーション関連のコンポーネントです：隣接するエッジに対して特定の角度内の動きを制限します。 バーチャルボディのモデリングは、人の姿勢を計算するために重要です。 正しく配置された制限のあるモデルでは、一連の正しいポーズを取得できます。これにより、よりリアルな動きを取得できます。 ほとんどのモデルは体の部分の硬さを暗示していますが、これは現実の近似にすぎません。

スケルトンは通常、エッジで接続されたソリッドセグメントの階層としてモデル化されます。各セグメントは、長さ、形状、体積、質量などのプロパティによって定義されます。 マニピュレータは、ロボットアームまたはアニメーションキャラクターのように、エッジで互いに結合されたソリッドノットから組み立てられたチェーンとしてモデル化されます。 インデックスiのボーンの各移動および/または回転は、チェーンの後続のすべての要素に影響します。 チェーンは次のように形式化できます。子のないすべてのノードはエンドポイントと呼ばれるべきです。 各エンドポイントについて、チェーンのルートノードが一致するまで（チェーンの開始）、スケルトンに沿って親から親へ移動することでチェーンを形成できます。 定義により、IKタスクは静的ルートノードを想定しています。 ただし、メソッドは通常、ルートの移動を処理します。



FABRIKアルゴリズムフルサイクルアルゴリズム（擬似コード、インデックス1の下の最初の配列要素） 
 :    p[i]  i = 1...n,   t      . d[i] = | p[i+1] - p[i] | for i = 1, ... , n-1  :   p[i], i = 1...n //     dist = | p[1] - t | //   if dist > d[1] + d[2] + ... + d[n-1] { //  for i = 1, ..., n-1 do { //  r[i]   t   p[i] r[i] = | t - p[i] | lambda[i] = d[i] / r[i] //    p[i] p[i+1] = (1 - lambda[i]) * p[i] + lambda[i] * t } } else { // ; .. b     p[1] b = p[1] //,        p[n]  //  t   (tolerance) DIFa = | p[n] - t | while DIFa > tol do { // 1 :   //   p[n]    (,   "   " - . .) p[n] = t for i=n -1 , ..., 1 do { //  r[i]   p[i]    p[i+1] r[i] = | p[i+1] - p[i] | lambda[i] = d[i] / r[i] //    p[i] p[i] = ( 1 - lambda[i]) * p[i+1] + lambda[i] * p[i] } // 2:   //   p[1]   p[i] = b for i=1 ,..., n - 1 do { //  r[i]   p[i+1]   p[i] r[i] = | p[i+1] - p[i] | lambda[i] = d[i] / r[i] //   p[i] p[i+1] = (1-lambda[i]) * p[i] + lambda[i] * p[i+1] } DIFa = | p[n] - t | } }






2.FABRIK-IK問題の新しいヒューリスティックソリューション

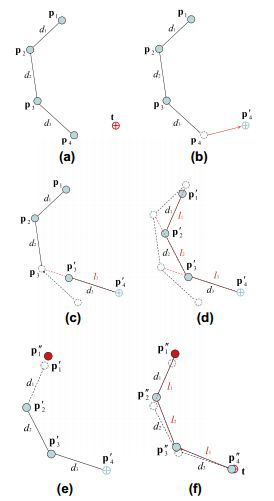このパートでは、FABRIKメソッドの本質を説明します。 順方向モードと逆方向モードですでに計算された位置を使用します。 FABRIKは、各ノードの角度を一度だけ調整することにより、エラーを最小限に抑えます。 つまり 最後のノードから始まる回路全体がバイパスされ、バイパスされた各ノードの角度調整が行われます。その後、回路はすでに反対方向にバイパスされます。 この方法は、回転回転とは対照的に、ノードの位置を見つけるタスクを直線上の点を見つける問題に変えます。 したがって、時間を節約し、計算量を減らすことができます。 セットp [1]、...、p [n]がマニピュレータのノードの位置のセットであると仮定します。 また、 p [1]がルートノードであり、 p [n]が最終ノードであるとします。 簡単にするために、1つのエンドノードを残します。 ターゲットはtと初期ベース位置bで表されます。 FABRIKメソッドは上記のリストに示されており、左の図の完全なサイクルをグラフィカルに解釈します。1つのターゲットポイントと4つのノードがチェーン内にあります。 図のアルゴリズムの全サイクルを検討してください。





詳細：

まず、ノード間の位置が考慮され（配列d ）、その後、ターゲットポイントが到達可能かどうかを確認するためのチェックが行われます。 ルートノードとターゲット間の距離（ dist ）が考慮され、この距離がノード間の距離の合計よりも小さい場合、目標は達成可能ですが、そうでない場合は達成できません。 目標が達成可能な場合、フルサイクルは2ステップに制限されます。 最初の段階で、アルゴリズムは、マニピュレータp [1]のベースに移動する有限要素p [n]から開始して、各ノードの初期位置を推定します。 したがって、ターゲット位置を終了ノードの位置p '[n] = tとします。 点p [n-1]とp '[n]の上にある線l [n-1]を取得します。 インデックスn-1のノードの新しい位置p '[n-1]は、このライン上でp' [n]から距離d [n-1 ]にあります。 同様に、インデックスn-2のノードの新しい位置p '[n-2 ]は、距離pの点[n-2]とp' [n-1]にある線l [n-2]を使用して計算できます。 d [n-2] from p '[n-1] 。 最後のノードを含むすべてのノードのすべての新しい位置が計算されるまで、アルゴリズムが繰り返されます。 ルート要素が必要な位置に移動する場合、FABRIKは前述のように機能しますが、唯一の違いはルートノードの新しい位置p '' [1]が初期位置ではなく目的の位置になることです。

1回の完全な反復の後、ほとんどすべての場合（観測による）、最終ノードはターゲットに近づきます。 この手順は、エンドノードがターゲットの位置に到達するか、ターゲットまでの許容距離に近づくまで、必要な回数だけ繰り返されます。 リミッターを導入せずにFABRIKメソッドを実装すると、目標が達成可能な場合、どのターゲットポイント/チェーンでも収束します。 ただし、チェーンが到達できるステーションからターゲットがさらに離れている場合、エンドノードの過去と現在の位置を比較し、エンドノードの変位が特定の値（イプシロン）より小さい場合にアルゴリズムを停止する中断条件が必要です。 また、特別な場合には、アルゴリズムは一定の反復回数が経過した後に中断されます（ただし、これまでのところ、この状況は発生していません）。

より高速な結果と複数の反復でのソリューションのために、等角幾何代数（CGA）を使用した最適化が可能です。 CGAは、球、線、平面、円など、代数オブジェクトによって非常に簡単に表示される基本的な形状に利点があります。 したがって、2つの既知のノードの間に位置するノードの位置の検索は、これらのノードに対応する位置に中心を持つ2つの球の交点、および目的のノードと使用可能なノードの位置間の距離に等しい半径で表現できます。 ノードの新しい位置は、2つの球の交差によって形成される円の最も近い点にあります。 もう1つの単純な最適化は、ターゲットが利用できないときにターゲットの方向に直線を構築することです。



3.多くの有限ノードを持つモデル

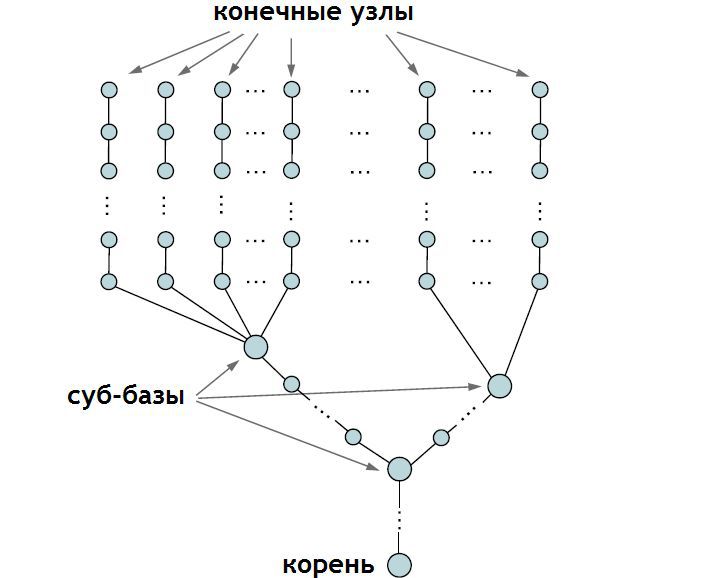1つのエンドノードの場合と同様に、アルゴリズムは2つの段階に分けられます。





4.リミッター

そして最後に、この記事の最もおいしい部分は、リミッターを使用した計算です。 ご想像のとおり、実際の生物との類似性を高めるために必要です。 通常、ノード自体は3つの自由度によって特徴付けられます。 ノードの回転は、最終位置を反映する「単純な回転」（2自由度）、および自身の軸を中心とした回転（1自由度）として特徴付けられます。 したがって、ノードの動きをこのような2つのフェーズに分割し、それらにリミッターを適用すると、ノードの位置を制御できます。 制限自体も同様の方法で課すことができます。 反復アルゴリズムの場合、アルゴリズムの各反復で回転制限を適用できます。 この場合、リミッターはアルゴリズムの収束に影響しません。 リミッターを使用する主なアイデアは、制限内でノードを再配置および再配置することです。



この手順は、移動制限のないバリアントが実行されたのと同じ方法で、すべてのノードに対して、直接および逆の順序で繰り返されます。 同時に、「楕円」制約はおそらくノードではなくエッジの特性です。つまり、 第2フェーズでは、ノードp [3]は楕円に移動する必要があります。 perev。


More articles:


All Articles