1.はじめに
私たちの世界では、すべてが相互に接続されており、互いに類似しており、同じまたは類似のパラメーターを持っています。 多くの場合、これらのプロパティは対称性と呼ばれます。 簡単なオックスフォード辞書では、対称性は「身体の一部または全体のバランス、バランス、類似性、調和、一貫性による美しさ」と定義されています。 [1]非常に頻繁に、対称性は数学と物理学に現れます。 物理学では、対称性は量子力学とその数学的な装置、例えばシュレディンガー方程式[2]で明らかに現れます。 数学には、類似性と対称性の概念で動作する特別な数学的装置があります。 この数学的装置は、群論と呼ばれます[3]。 数学における対称性の実用的なアプリケーションの1つは、公開キー暗号化「RSA」です[4]。
2.残差素数の行列
控除と比較法の定義を考慮してください。 これは、現代の説明辞書で与えられている定義です。 差「a-b」を「m」で割った場合、数字「a」は「m」を法とする数字「b」の剰余と呼ばれます(a、b、m> 0は整数)。 つまり、「a」は「m」を法とする「b」に相当します。
a≡b(mod m)
これは、「a」が「m」で完全に割り切れない場合、「b」は「a」を「m」で割った余りであることを意味します。 2つの整数「a」と「b」は、正の整数「m」を法として比較できます。「m」で割ると、同じ残基が得られます。
素数を取り、「b」で示します。 間隔(1,2,3、... b-1)の整数のセットは、「B」で示されます。 このセットが列の形式で、下から上に昇順で記述されている場合、マトリックス列を取得します。 この列のすべての番号は次々に配置され、番号は「b-1」です。 この列を数字「1」で示します。 セット「B」の各数値は2乗され、残りを「b」で除算します。 除算の結果の剰余は列に書き込まれます。 この列を番号「2」で示し、列番号「1」の右側に配置します。 残基を2乗した数に対応し、それらと同じ線上にあるように残基を配置する必要があります。 その後、各数値をセット「B」から3乗し、残りを「b」で除算します。 得られた残基から、列番号「2」と同様に、番号「3」の下に列を形成します。 次に、類推により、次の段階に進み、「b」による除算の残りを見つけます。 セット「B」から数値を構成する指数が「b」より小さくなるまで、アクションを実行します。 結果として、サイズ(b-1)x(b-1)の正方行列を取得します。
プライム整数「b = 23」のそのような正方行列の例を図1に示します。
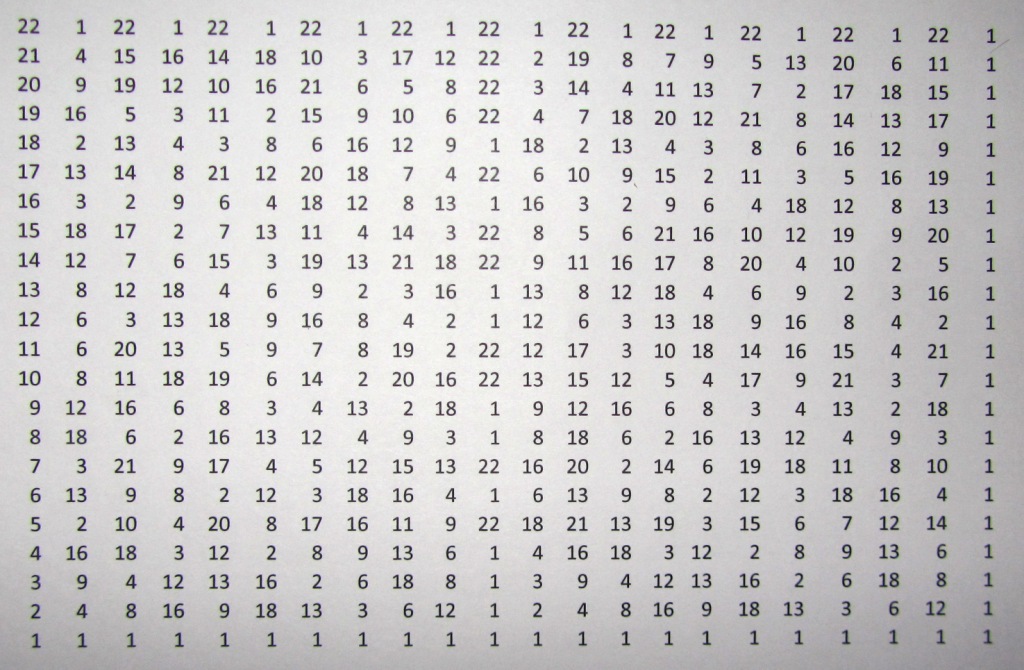
図 1素数整数b = 23の残差の行列。
結果のマトリックスには驚くべき特性があります:
-マトリックスの最後の列が1つのユニットで構成されていることが明確にわかります。 これは、フェルマーの単純性テストと完全に一致しています。 A n-1≡1(mod N)[5]。
-番号(b-1)/ 2(「b」から1を2で割った値)の列は、セット「B」の2つの値のみで構成されていることに注意してください。 これらは値1および(b-1)です。
-列の「B」を設定する数値の値は、間隔の中央で対称です。つまり、 値のペア(b-1)/ 2および(b + 1)/ 2。
-異なる列の対称性のタイプは異なります。
-偶数の列の場合、値は間隔の中央から等距離にあります。 値のペア(b-1)/ 2と(b + 1)/ 2は一致します。 図に示すマトリックスの場合 1、11の2乗を23で割った余り、12の2乗を23で割った余りは同じで、6に等しい
-奇数の列の場合、間隔の中央から等距離の値、つまり 値のペア(b-1)/ 2と(b + 1)/ 2の合計は、常に「b」に等しくなります。 図に示すマトリックスの場合 図1の場合、23で割った3次の11の剰余は20、23で割った3次の12の剰余は3です。合計で、これらの2つの残基は23です。 「b」に等しい。
上記で説明され、図に示されているマトリックスで考慮されているすべてのプロパティ 1は、他の素数整数と同じ規則に従って構築された行列に固有のものです。
3.合成数の残差のマトリックス
セクション2で考慮される行列は、素数の対称性を特徴づけます。 合成数の場合、同じルールで構築されたマトリックスは大きく異なります。 プライムマトリックスのプロパティを継承しますが、新しいプロパティも取得します。 2つの素数「x」と「y」の積である化合物番号を考えます。 同様に、数値の値は「b」で示され、間隔(1、b-1)内のすべての数値のセットは「B」で示されます。 素数「x = 5」と「y = 7」を乗算した結果である複合数「b = 35」を考えてみましょう。 数値間隔(35-1)のさまざまな次数の残基の行列を作成します。 残基のマトリックスを図に示します。 2

図 2合成数b = 35の残基の行列。
一部のプロパティは、残差素数のマトリックスから継承されます。 たとえば、列に存在する数値の値は、数値間隔の値の中央に対して対称です。 値(b-1)/ 2および(b + 1)/ 2。
図に示すマトリックス。 2、新しいプロパティを持ちます:
-行列の行の値。最初の列には合成数の約数の倍数があり、数値は合成数の約数の倍数であり、1には決してなりません。たとえば、図 2、2列目の5行目の値は25、3行目の20、4行目の30などです。 これらの値はすべて5の倍数です。
-値が「b」の約数の倍数である行を除外する場合、残りの値が1である2つの列が必ずあります。 2は、番号が12、24の列です。
-これらの選択された2つの列のうち、最大の列番号は(x-1)x(y-1)の積です。 つまり 各係数から1を減算して乗算すると、選択された最大の列の番号が取得されます。 図のマトリックスの場合 数「b」の2つの要素は5と7です。それぞれから1を減算して乗算すると、(5-1)x(7-1)= 24になります。これは、選択された最大列の数です。 この場合、列番号はオイラー関数に等しく、その値は(x-1)x(y-1)= =(n)であることに注意してください。 [6]。
-2つの列には必ず4つの値が存在します。素数の残差の行列と(1、b-1)に等しいセット「B」の値の場合、2番目の列の値は1になります。 「B」を設定します。2乗して「b」で割ると、余りは1になります。 2は番号6と29です。
-常に数字のペアがあり、セット「B」が互いに続き、その値は数字「b」の約数「x」と「y」の倍数です。 図のマトリックスの場合 2はペア(14、15)と(20、21)です。
上記で説明され、図に示されているマトリックスで考慮されているすべてのプロパティ 2、他の合成整数の同じ規則に従って構築された行列に固有です。
4.数値の因数分解
RSA公開鍵暗号化方式[4]を検討する場合、その使用は、合成数の残差行列内の相互に反対のマッピングの存在に基づいています。 合成数「b」を取得すると、その残差行列には「c」と「d」という2つの列が常に存在し、次の条件が満たされます。
(b1 ** c)≡c1(mod b); (c1 ** d)≡d1(mod b); b1 = d1
ここで、b1、c1、d1は列1、c、dの数値です。
つまり、複合番号「b」には、範囲(1、b-1)から常に2つの番号「c」、「d」があり、アクションのシーケンスは真です。
-範囲(1、b-1)の任意の数値「b1」の余りを、「c」で累乗し、「b」で割った値を求めます。 この残りを「c1」で示します。
-結果の剰余「c1」を「d」の累乗にし、剰余で「b」で除算します。 この残りを「d1」で示します。
-結果の剰余「d1」は常に「b1」に等しくなります。
RSA暗号化アルゴリズムの場合、(c、b)は公開鍵、(d、b)は秘密鍵です。

図 3合成数b = 33の残基のマトリックス。
図bの数b = 33の残差のマトリックスを考えます。 3.この数、c = 3、d = 7。 最初の列から任意の数、たとえば8を取得し、3度に上げます。残りは17です。数17は7の累乗になり、残りは8です。 この余りは、最初の列の元の数に等しくなります。
RSAは、一般的な公開キー暗号化アルゴリズムの1つです。 暗号化方法の改善とともに、秘密のメッセージを解読する方法も改善されています。
多くの場合、彼らはRSA額の復号化タスク、つまり ベース化合物番号の約数を見つけます。 これらの方法は、数値の因数分解と呼ばれます。 値の単純な列挙と数値の検証に加えて、二次ふるい法を使用します。
この方法の基本は、2乗および数値「b」による除算の残差の一部が数値の完全な2乗であることです。 図 2つの完全な正方形は、最初の列の数値(11、12、17)の2次剰余です。 数「b」の約数を見つけるには、2次剰余から平方根を抽出する必要があります。 結果、つまり 平方根、数値「b」から減算するか、数値「b」に加算します。 「b」の約数の倍数が取得されます。 ユークリッドアルゴリズムを使用すると、数値「b」の約数を見つけることができます。
図 2、11の2次余剰は16です。16から平方根を抽出します。4です。11に4を追加すると、15が得られます。数は除数5の倍数です。
数値の因数分解の最も現代的な方法の1つは、数値フィールドのふるい法です[7]。 この方法により、チェックされる値の数を減らし、計算時間を短縮できます。 数値フィールドのふるい法と合成数の残差行列の特性を使用して、さらに重要な結果を得ることができます。
数値の因数分解方法の実験的検証には、いわゆるメルセンヌ数[8]を使用できます。 これらの数字は、2の「n」のべき乗から1を引いた数を表します。「n」は自然数です。 限られた数のメルセンヌ数のみが素数であり、残りは有限数の約数に分解されます。
良い例として、約数の1つである4099の次数2から1を引いた値は-
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717675764345142
549580867720367836084289513946899287311856029114297
4.文学
[1] Dエリオット、P。ドーバー「Symmetry in Physics vol。1」、MIR Publishing House、1983年。
[2]「シュレディンガー方程式」、en.wikipedia.org / wiki /シュレディンガー方程式。
[3]追伸 アレクサンドロフ、「グループ理論の紹介」、モスクワ科学、GRFML、1980。
[4]「RSA」、en.wikipedia.org / wiki / RSA。
[5]「農場テスト」、en.wikipedia.org / wiki / Test_Farm。
[6]「オイラー関数」、http://ru.wikipedia.org/wiki/Euler_Function。
[7]「数値フィールドをふるい分ける一般的な方法」、en.wikipedia.org / wiki / General_Numeric_ Field_Grid_Method。
[8]「Mersenne Numbers」、http://ru.wikipedia.org/wiki/Mersenna_Numbers。