
多くの人がFlappy Birdをプレイしようとしました。 50本のパイプで飛ぶ人はほとんどいません。 ハブを含むボットを作成しようとした人もいました 驚くべきことに、インターネットで見つけられる最も成功したボットでさえ、結果はあまり印象的ではありません-約160ポイントです。 質問が発生しますが、一般的にFlappy Birdを無期限にプレイすることは可能ですか? それとも、経験豊富なプレイヤー/理想的なボットでさえ克服できない一連の障害がある可能性は、わずかではありますが、常に可能です。
そして、ここで数学が助けになります。 Flappy Birdの勝利戦略を見つけましょう。
モデル
ゲームの数学モデルについて説明します。 私たちの競技場は飛行機です。 鳥がいます-座標軸に平行な長さwの辺を持つ正方形。 障害物-パイプ-高さh ギャップの水平開口部を持つ幅w チューブの垂直ストライプがあります。 2つの隣接する障害物間の水平距離は固定されており、Δtubeに等しくなります。 各パイプの水平開口部の位置はランダムです(一定の範囲で均等に)。 さらに、床があります-水平線f。 セックスも障害です。 写真:
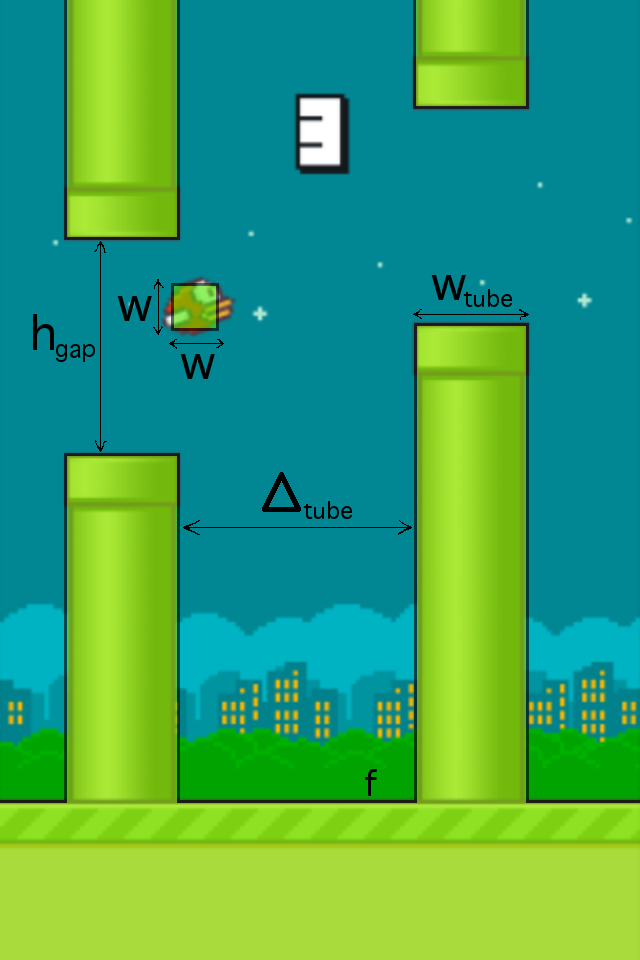
鳥の水平速度は一定であり、v xに等しくなります。 重力は鳥にも作用し、鳥に垂直加速度gを与えます。 最初は、鳥の垂直速度は0です。毎回、プレイヤーはタップを行うことができます。つまり、鳥の垂直速度をv jumpにします。 さらに、一種の空気抵抗が鳥に作用します。垂直速度は、一定のv fallによって下から制限されます。 実際、これは、各タップの後に、鳥が放物線に沿って移動し、ある点で直線になることを意味します。 タパの後に鳥が移動する軌道をパダボラ(落下放物線)と呼びます。 次のようになります。
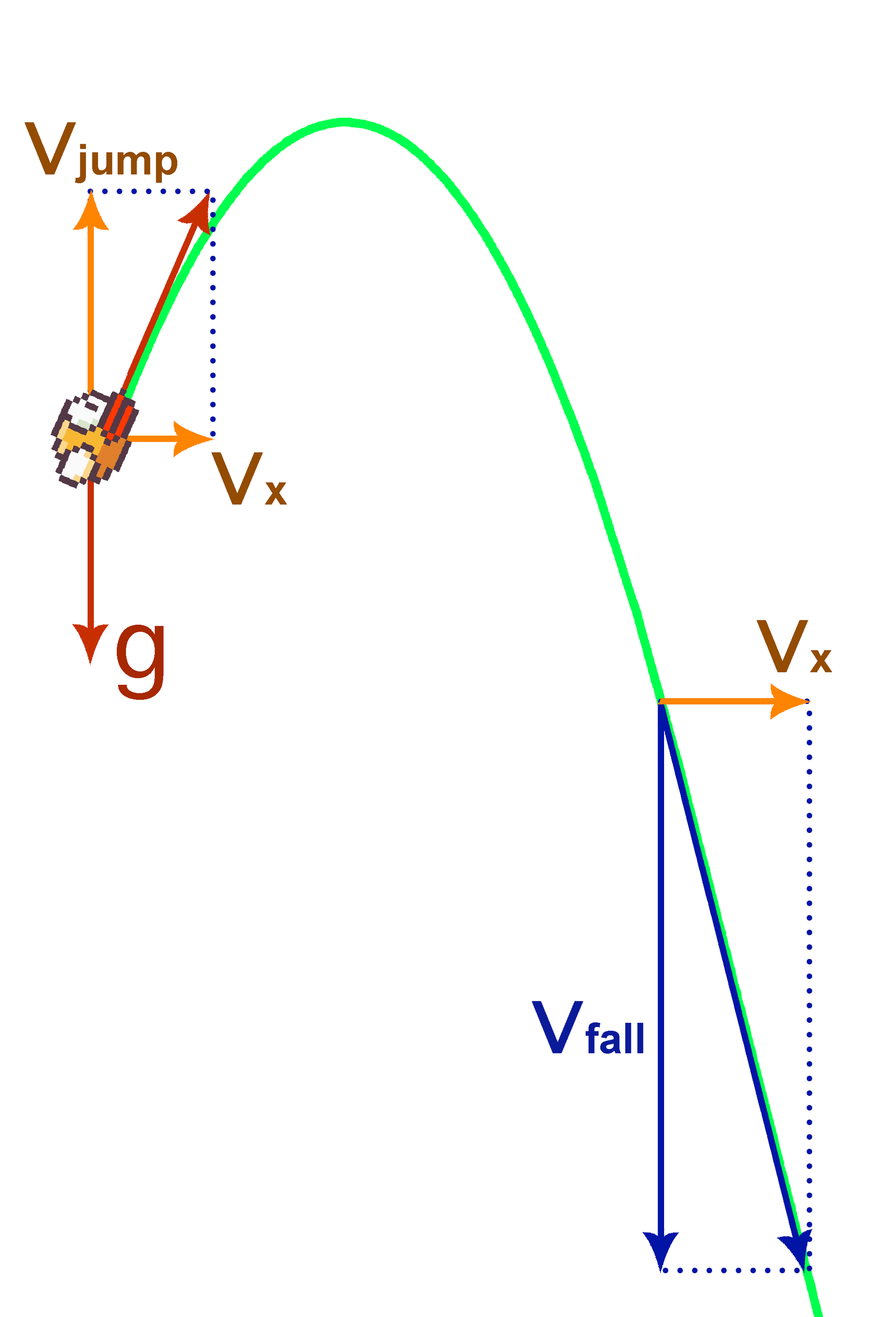
鳥が障害物に触れると、ゲームは終了します。 プレーヤーの仕事は、移動距離を最大化することです。
追い越しの戦略に移る前に、1つのトリックをやってみましょう。 四角い鳥と障害物の交差を分析することはあまり便利ではありません。 しかし、鳥がポイントである同等のモデルに簡単に切り替えることができます。 これを行うには、障害物を「膨らませる」と同時に、鳥をポイント(最初の正方形の中心)のサイズまで「吹き飛ばす」だけで十分です。 この場合、新しいポイントバードが腫れた障害物にある場合にのみ、最初の正方形は障害物と交差します。 写真:
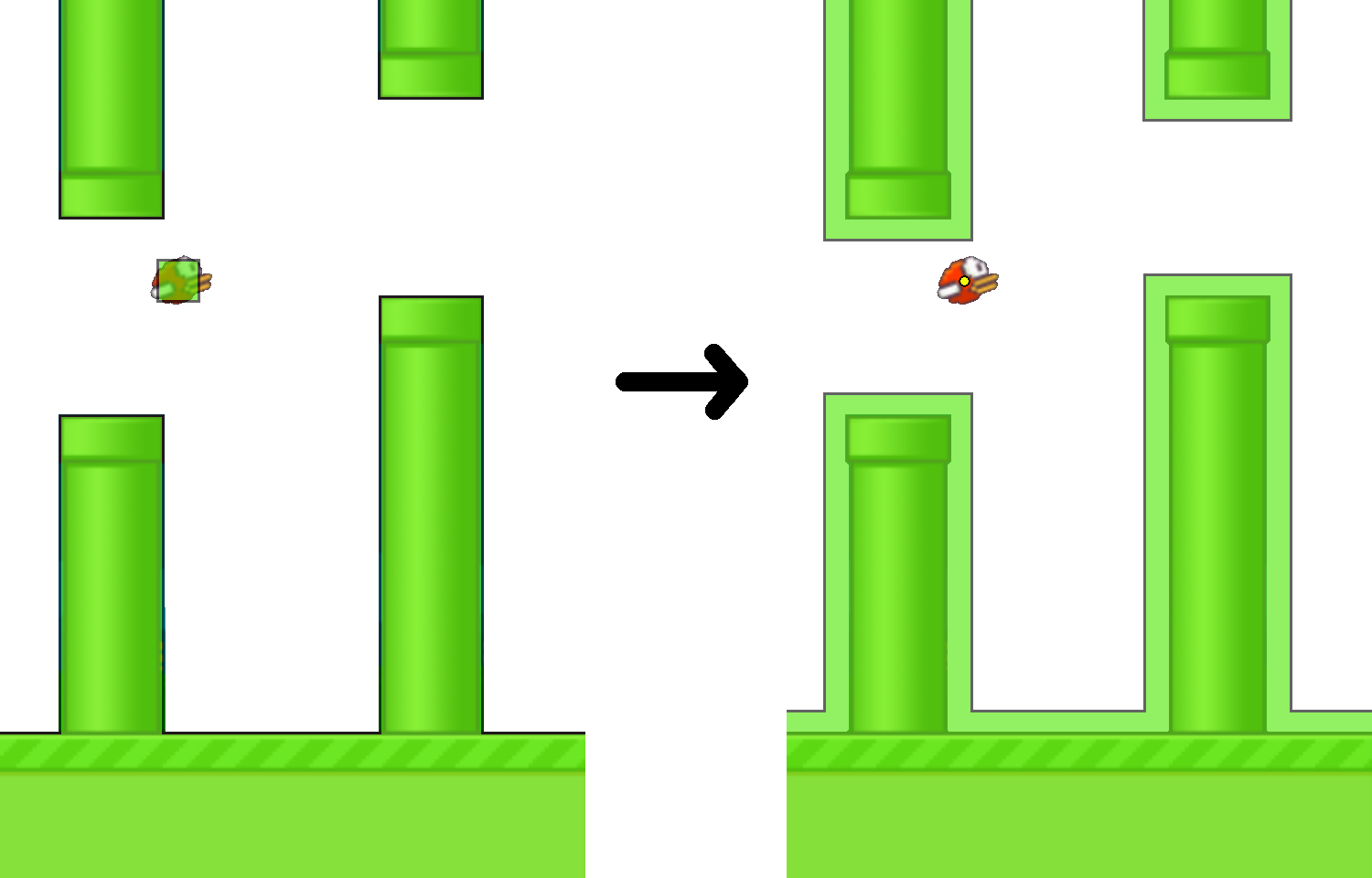
科学的に、障害を「膨らませた」結果はミンコフスキー和と呼ばれます。
ミンコフスキー和
ウィキペディアのレポート:
線形空間Vの2つのサブセットAとBのミンコフスキー和は、AとBのすべての可能なベクトルの和で構成される集合Cです。C= {c | c = a + b、a∈A、b∈B}
日常の観点から、図Aと図Bのミンコフスキー和は、図Aが各点Bに取り付けられている場合に得られる図であると仮定できます-右図を参照してください。
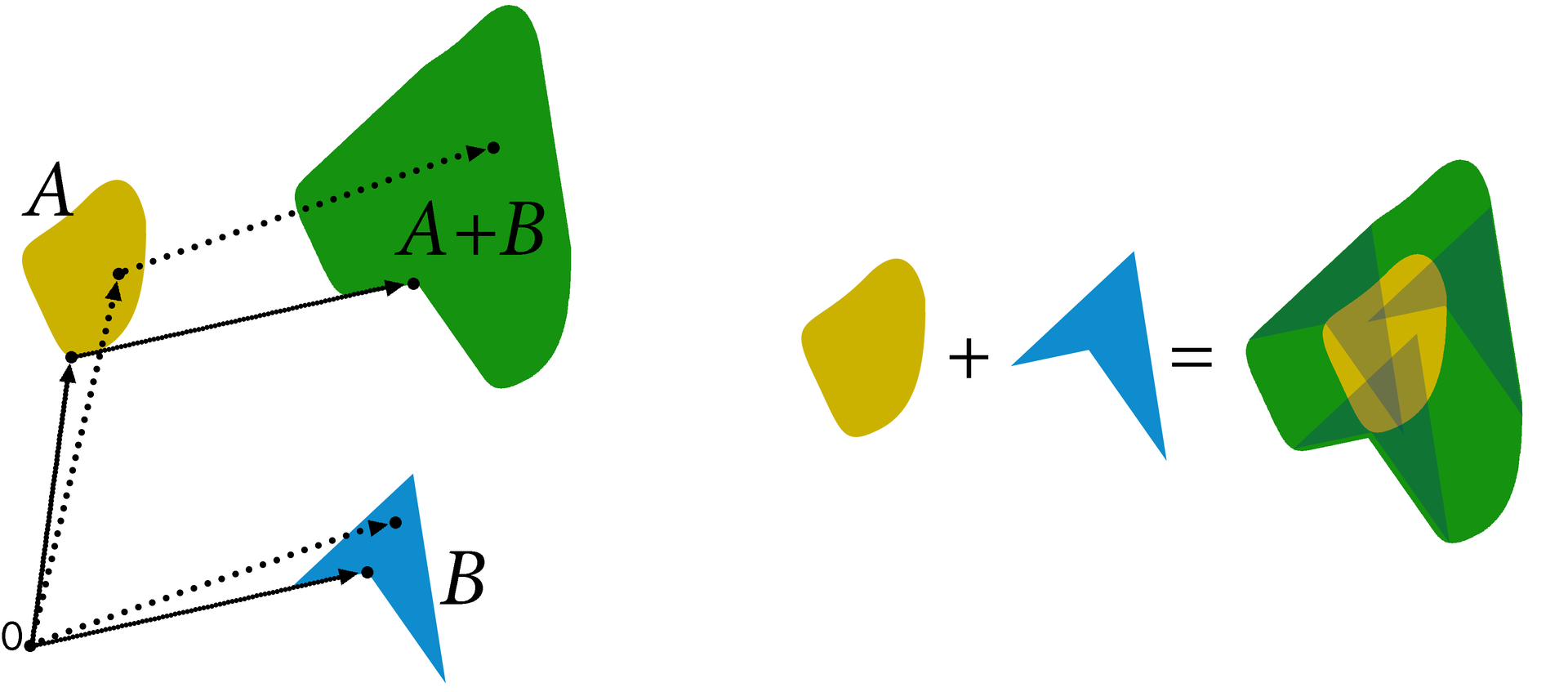
逆パダボラ
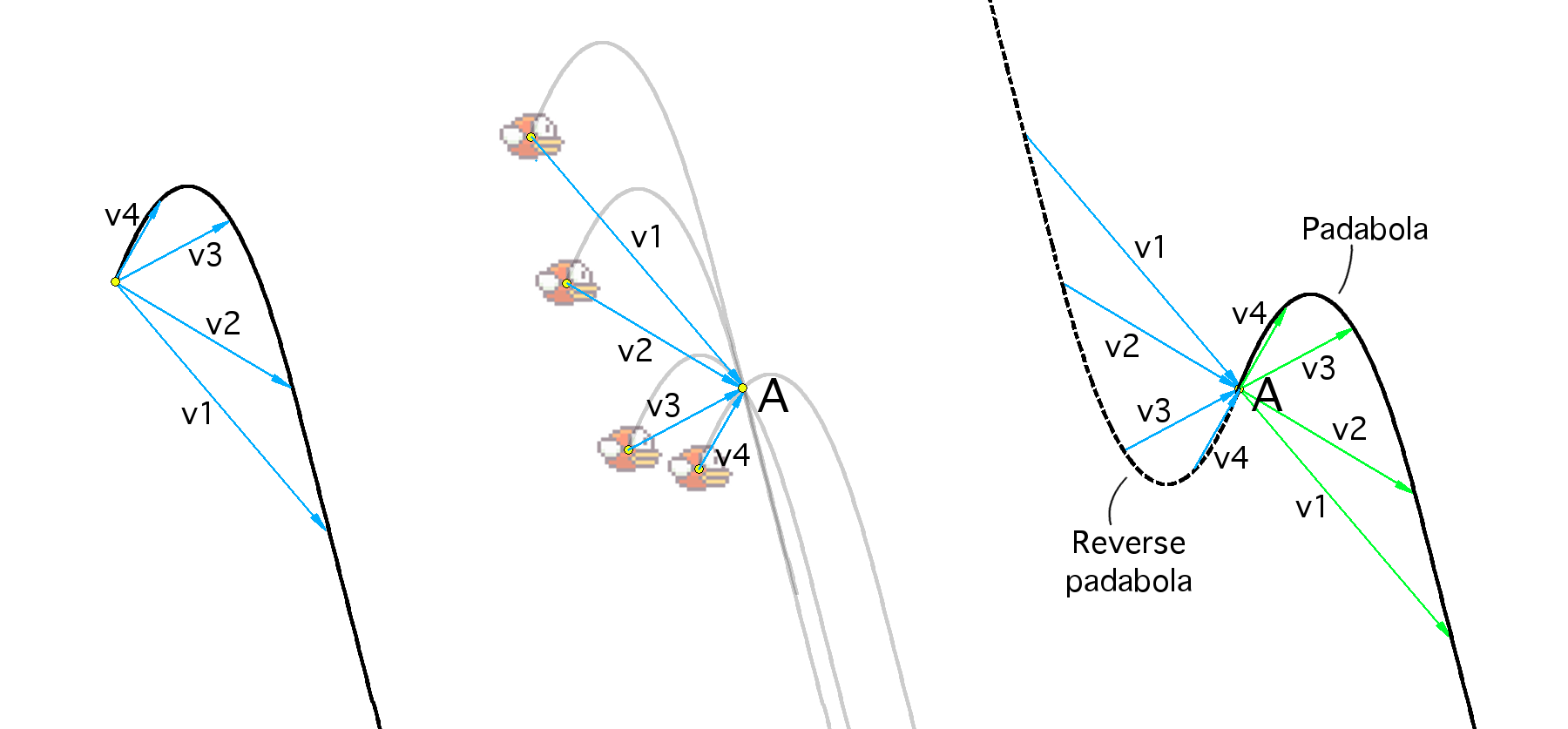
補助的な問題を解決しましょう:鳥がタップした後、指定されたポイントAを飛ぶように鳥はどこにいるべきですか? より正確には、ポイントから描画されたパダボールが固定ポイントAを通過するように、ポイントの幾何学的位置を見つける必要があります。中央の図を参照してください。 v⃗をパダボラの開始点とその点の1つを結ぶ任意のベクトルとします。 ポイントA-v⃗でタップした後、鳥がポイントAを飛ぶことは簡単にわかります。つまり、A-v⃗はポイントの望ましい幾何学的位置に属します。 さらに、あらゆる種類のベクトルv⃗を使用して、必要なすべてのポイントを取得します。 しかし、フォームA-v formの点のセットは何ですか?vはパダボラの点の1つに対するベクトルの半径ですか? これは、ポイントAを基準に反射した後、パダボラに対して中心的に対称なパスです。ところで、画像では、より明確になっています。
問題を一般化できます。特定のエリアSを飛行するには、どこをタップする必要がありますか? 上記に基づいて、答えはミンコフスキー領域Sと逆パダボラの合計です。
上部の障害
最後に、主なタスク-勝利戦略の発見に目を向けます。 最初に簡単なケースで解決します。 モデルにパイプと床の下半分がないようにします。 つまり、障害物の上部のみがあります。 パイプの上半分が自立していることを考慮してください。 鳥はこの障害物の左のどこかで旅を始めましょう。 ある時点で、鳥がパイプに衝突したとします。 前の段落からわかるように、これは、障害物に逆パダボラを追加することによって得られた領域でタップが行われたことを意味します。 結果の領域を青で色付けします。 図:

プレーヤーが青い領域のある点で触れた場合、対応するパダボラは最初に障害物と交差し、その後、青い領域を離れるだけであることに注意してください。 言い換えれば、プレイヤーは青い領域を失うか、もう一度タップすることを余儀なくされます。 さて、単一の青い領域は右に制限されているため、無限に飛行しても機能せず、最終的には鳥は死にます。 したがって、青い領域をタップすると、常に敗北につながります。 さらに、青い領域の外側のタパスは損失につながることはありません。青い領域をタップしないと、上部の障害物に衝突することはできません。また、鳥が飛ぶのを防ぐ方法はありません。
その結果、上部障害物のみの場合、次のステートメントを取得します。
声明 鳥が青いエリアのプールの外で飛行を開始した場合、無限の勝利戦略が存在します。 そして、すべての勝ち戦略は次のように説明されています。青いエリアの外側ではプレイヤーは任意の決定を下すことができ、青いエリアではプレイヤーはタップできません。
低い障害
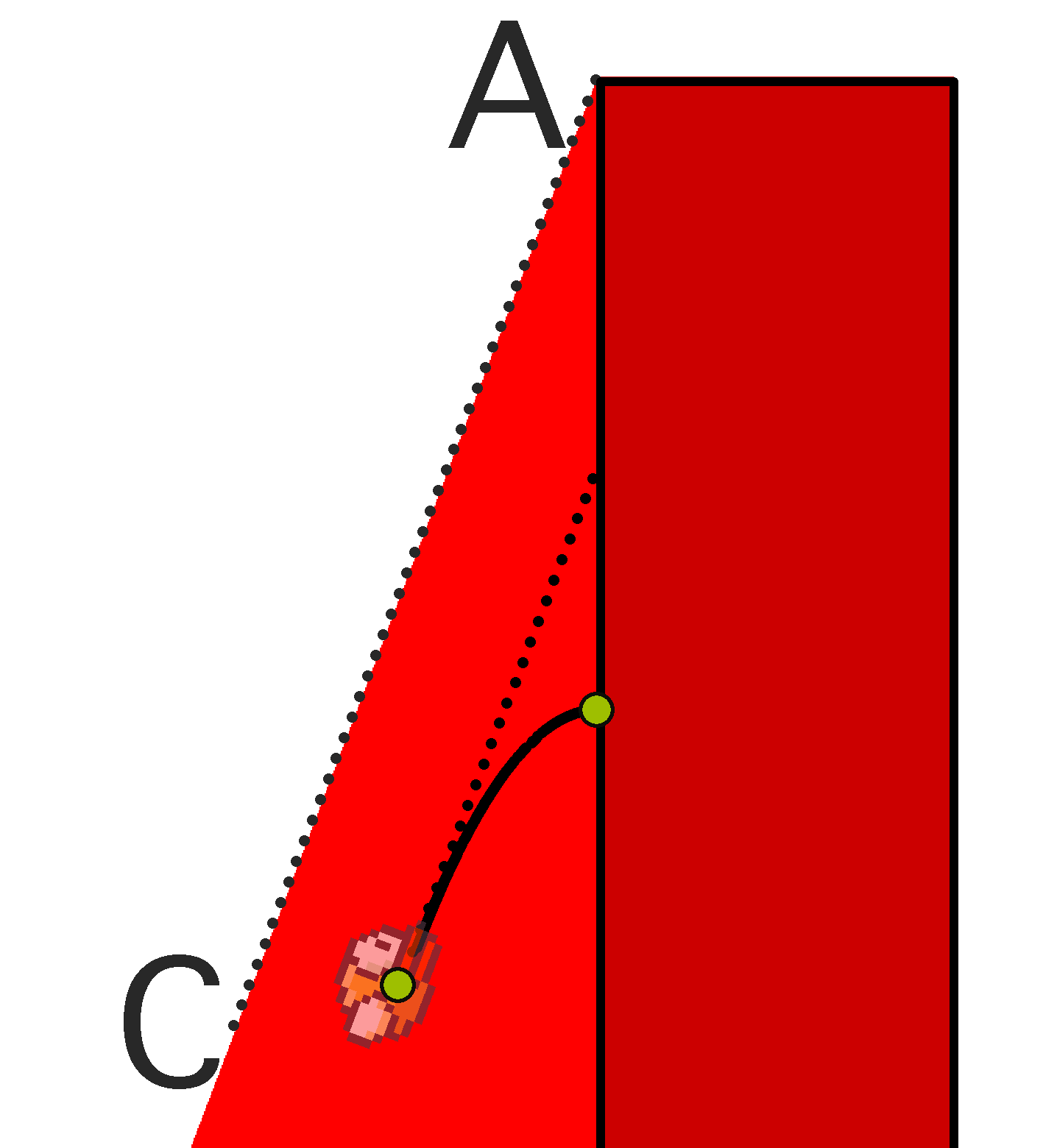
ここで、パイプの下半分のみがモデルに存在する場合を考えます。 つまり、上半分とセックスはありません。 繰り返しますが、別の低い障害物を考慮してください。 ACビームを左上隅(点A)から描きます。その傾斜角はatan(v jump / v x )です。つまり、タップ直後の鳥の速度に沿って向けられたビームです。 鳥がACビームの下にくるようにします。 その後、プレーヤーのアクションに関係なく、v jumpよりも高い垂直速度で上昇することはできません。 一定の水平速度v xが与えられると、これは障害物との避けられない衝突、つまり損失につながります。 下部の障害物とACビームの下の領域を赤で塗りつぶします。 得られた赤いスライドは次のとおりです。
勝利戦略では、鳥が赤いエリアに落ちてはいけないことがわかります。 さらに、ある時点で鳥が赤い領域の外側にいる場合、その鳥は任意の時間、その外側に留まることができます。 実際、常に赤い領域の境界に近づくと、プレーヤーはそこに入らないほど頻繁にタップを開始できます。
床を追加します。 床が下半平面の形で別の赤い領域として認識されることは簡単にわかります。
したがって、より低い障害物と床のみが存在する場合、それは真実です。
声明 最初の瞬間の鳥が赤い領域の結合の外側にある場合、無限の勝利戦略があります。 すべての勝利戦略は次のように定式化できます。赤いエリアの外側では、プレーヤーは任意の決定を下すことができ、赤いエリアに近づくと、プレーヤーはタップする必要があります。
すべての障害が一緒に
一般的な状況を考慮してください。 パイプの上半分、下半分、床があるとしましょう。 次のことが理解できます。
声明 青の領域の結合が赤の結合と交差せず、鳥が最初に青と赤の領域の外側にある場合、勝利戦略があります。 勝利戦略は次のように説明されます。青と赤のエリア以外では、決定を下すことができ、青のエリアをタップすることはできません。赤のエリアに近づくと、タップする必要があります。
このような戦略が存在するためには、青と赤の領域の交差が存在しないことが不可欠です。 実際、青い領域を飛んでいる鳥が赤い境界線の近くに来ることがあります-この場合、プレイヤーがタップすると、彼は負け、タップしないと、彼も負けます。
問題は、実際のゲームで青と赤の領域が交差するかどうかです。 時々交差することが判明しました。 そして、これは正確に1つの場合に起こります:隣接する2つのパイプの開口部の高さの差が十分に大きい場合。

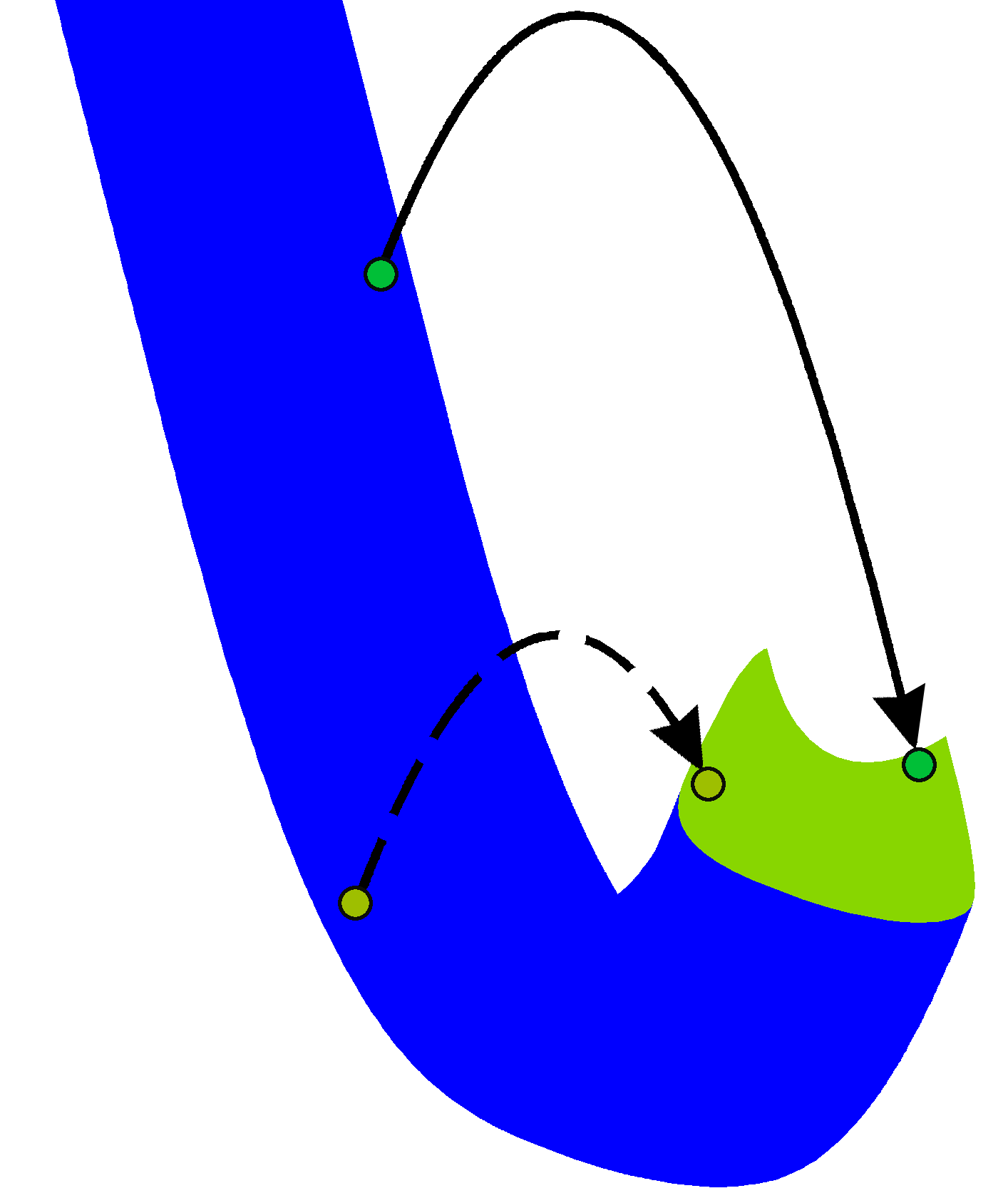
この状況を分析しましょう。 鳥がなんとかこれらのパイプを飛ぶようにします。 そのため、ある時点で彼女はセグメントABを横断しました。 しかし、これはポイントAとBから描かれた逆パダドールの間の領域でタップが行われたことを意味します。同時に、このタップは青色領域でも赤色領域でも作成できませんでした。 図に黄色で示されている領域のみが残ります。
つまり、勝利戦略の存在のために、あなたは黄色のエリアに入ることを保証することができる必要があります。 あとはタップするだけで、危険なセクションは克服されます。 常に黄色の領域に入ることができるかどうかを理解するために、逆パダドラでそれを追加します-黄色の1タップに到達するのに十分な領域(図では緑色)を取得します。 ある時点で、線の上にある点でタップが行われた場合、黄色の領域に入ることができないことに注意してください。 逆に、この境界より下の任意のポイントについては、連続して十分な回数タップすることでいつでも緑のエリアに登り、次に一度タップすることで黄色のエリアに入り、それに応じて障害を克服することができます。 言い換えれば、私たちの専門用語で線Gの上にあるポイントは青く塗られるべきです。 確かに、湾曲した三角形XYZを除き、ほとんどの部分はすでに青です。 青色の染料XYZ。 ここで、勝利戦略を策定するために、フレーズを追加する必要があります。鳥が黄色の領域にいる場合、鳥がこの領域を出る前に少なくとも1回タップする必要があります。
青の三角形の追加の色付けは、赤と青の領域の交差を追加できなかったため、ゲーム全体の開通性の分析には影響しなかったことに注意してください。
その結果、一般的なケースでは次のようになります。
声明 鳥が最初の瞬間に青と赤の領域外にいるようにします。 次に、無限の勝利戦略があります。 このような戦略はすべて次のように説明できます。青と赤の領域の外側では、いつでもタップできます。 青色の領域ではタップできません。 赤に近づいたら、タップする必要があります。 黄色の領域に入ったら、終了する前に少なくとも1回タップする必要があります。
興味深いことに、種が特定のラインの上を飛んで鳥が落ちるとすぐにタッピングを開始する戦略(たとえば、赤い領域の上部の境界線をわずかに上方に移動するのは論理的です)には、どのラインにも勝ち線はありません。
練習する
これはすべて良いことですが、実用的な結果が欲しいのです。 すでにハブに筋金入りのボットがあったので、ソフトウェアを作成することにしました。 偶然にも、Tappinatorと呼ばれるクローンのコードが手元にありました。その物理モデルは元のゲームに非常に近いものでした-彼らは試し、測定しました。 確かに、丸い鳥がいます(ゆるい鳥では丸いかもしれませんが、違いは小さく、四角い鳥で説明する方が簡単です)。 これは、丸い鳥の障害が「うねる」方法です。

その結果、青と赤の領域は次のとおりです。

黄色の領域については、標準的なパイプでも発生しますが、下から上に向けられた斜めの障害物の場合にも発生します(湾曲した青い三角形と一般的に):

まあ、実際には、ボットを使用したビデオ:
ビデオでは、50羽の鳥が1000匹に到達するまでの様子、ボットの視点から見たあらゆる種類の色付きの領域、1000羽の鳥が同時に飛んだ場合のゲームの様子を見ることができます。 ペイントされていない領域では、ボットはランダムに動作します。各ボットは、特定の時間にジャンプすることを決定する独自の固定確率を持っています。 ボットの観点からは、色付きの領域が数学の観点からよりもわずかに大きいことがわかります。 実際には、ボットは1秒間に60回しか意思決定を行うことができず、物理モデルも個別に更新されます。
おわりに
そのため、Flappy Birdのような単純なゲームでさえ、数学理論を開発する場所があることがわかりました。 実際、この瞬間から最も興味深いのは始まったばかりです。 次に、任意の形状の障害物をどのように処理するかという問題が発生します。ここでは、紫色の影、赤紫色の境界線、右線形接続領域、右線形接続閉鎖などの概念を導入する必要があります。 また、人が無限にプレイできるようにするために、人がどのような反応をするべきか(つまり、タパスで有効な時間誤差となるもの)が興味深いです。 ちなみに、これは極めて重要な質問であり、厳密な答えはまだわかりません。