ポアンカレは、2003年にのみ仮説を証明することができました。 その証拠は、同胞のグレゴリー・ペレルマンに属します。 この講義では、仮説の定式化に必要なオブジェクト、証拠の検索の歴史、およびその主要なアイデアに光を当てます。
モスクワ州立大学の力学と数学の学部の准教授によって講義が行われます 。 n アレクサンダージェグロフと博士 n ヒョードル・ポペレンスキー。
数学的詳細に入らない場合、ポアンカレ仮説によって提起された問題は次のようになります:(3次元)球体をどのように特徴付けますか? この質問を正しく理解するには、トポロジの最も重要な概念の1つである同相写像に精通する必要があります。 それを処理した後、ポアンカレ予想を正確に定式化できます。

正式な定義の数学的な詳細にまったく入らないようにするために、これらの図の点の間でそのような1対1の対応を確立することができる場合、2つの図は同相と見なされ、1つの図の近い点は別の図の近い点に対応し、逆も同様です。 省略した詳細は、ポイントの近接性の適切な形式化に正確にあります。
2つの図形の一方が任意の変形によって得られる場合、2つの図形が同相であることを理解するのは簡単です。

たとえば、上の図に示すように、ディスクから半球を取得するには、外側の縁を保持しながら、上から中央に向かって押すだけです。 表面は完璧なゴムでできているので、すべての形状を好きなように圧縮して引き伸ばすことができます。 涙と接着剤の2つのことしかできません。
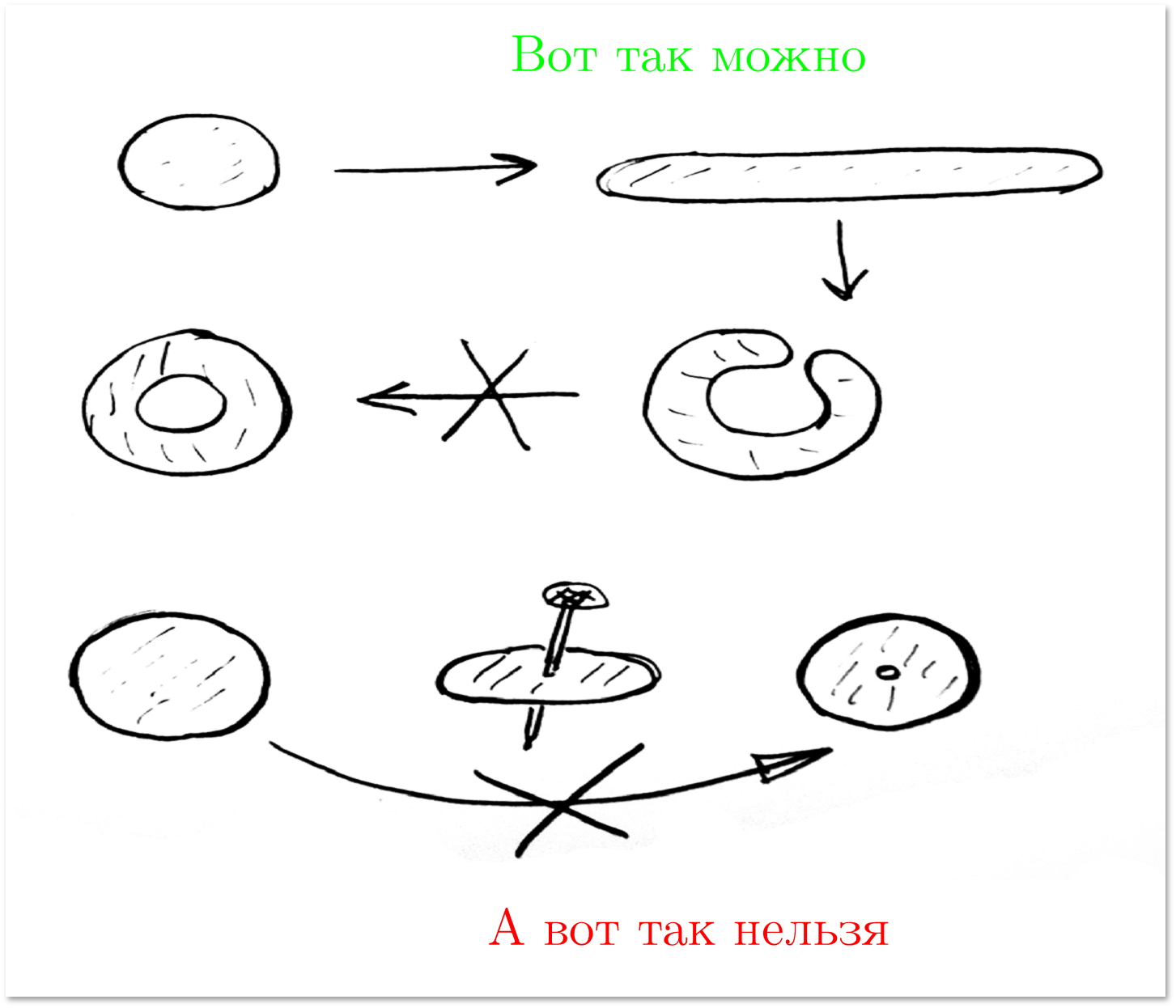
もう1つの操作を許可すると、より正確な(厳密さの観点からはまだ最終的ではない)同相図形のアイデアが得られます:図形にカット、ツイスト、タイ、ネクタイなどを作成できますが、カットを次のようにシールする必要がありますだった。
もう1つの例を示します。 虫が結び目と小さな洞窟の形で通路をかじったリンゴを想像してください。

トポロジの観点から、このリンゴの表面は球体のままです。 特定の方法でそれをすべて引き離すと、虫の食べ始める前と同じ形でリンゴの表面が得られます。
統合するには、ラテンアルファベットの文字を同相まで分類してみてください(つまり、どの文字が同相かそうでないかを調べます)。 答えは文字のスタイル(フォントのタイプまたは書体による)に依存し、スタイルの最も単純なバージョンについては次の図に示されています。

26文字から8つのクラスのみを取得します。
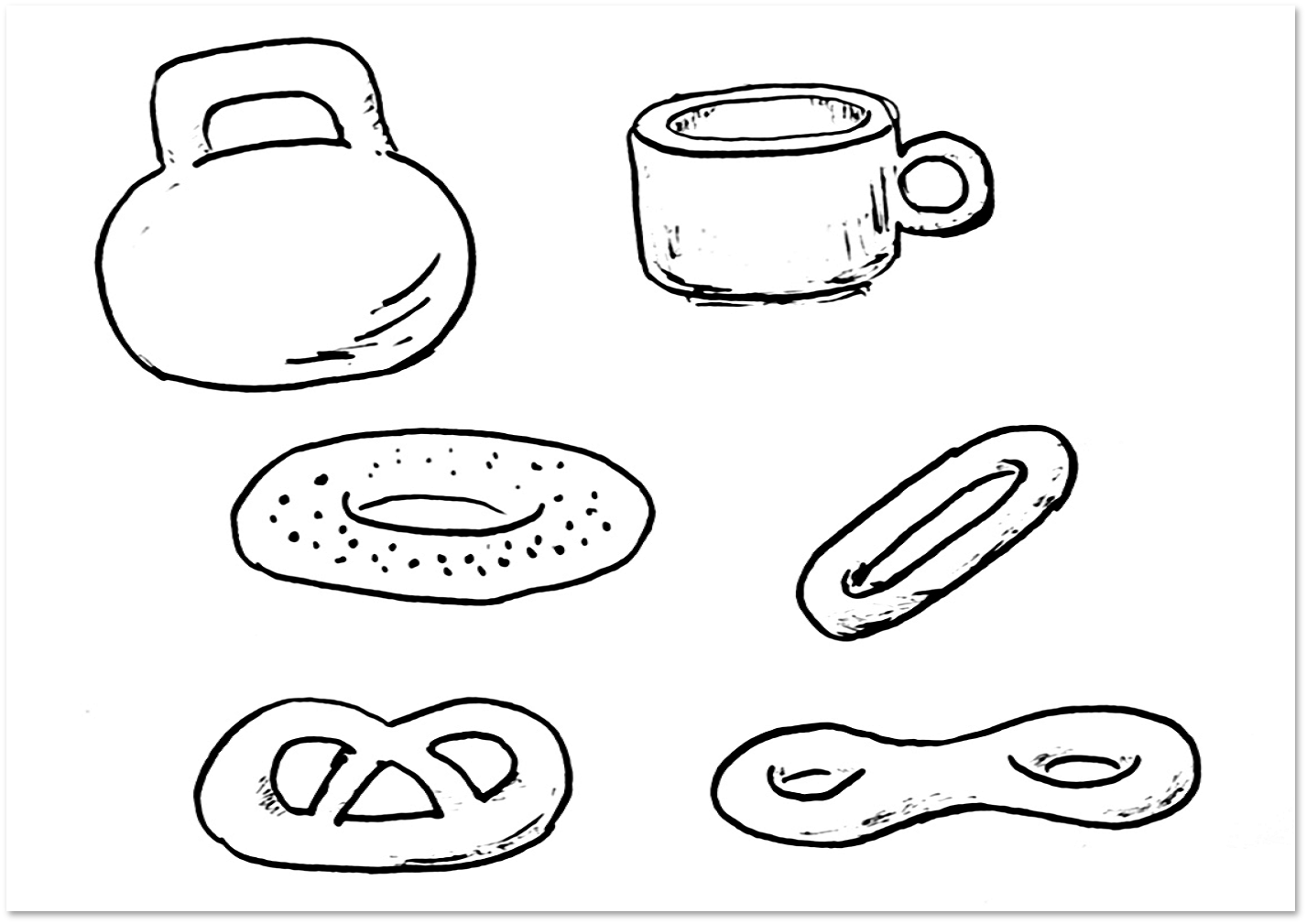
次の図は、ケトルベル、コーヒーカップ、ベーグル、ドライヤー、プレッツェルを示しています。 トポロジーの観点から見ると、おもり、コーヒーカップ、ベーグル、乾燥の表面は同じです。 同相。 プレッツェルについては、トポロジーとよく比較される表面との比較のためにここに示されています(図の右下隅に描かれています)。 おそらく既に理解しているように、トポロジカルプレッツェルと食用プレッツェルはどちらもトーラスとは異なります。
正式な質問
Mを次元3の閉じた連結多様体とし、そのループを点に縮約するようにします。 次に、Mは3次元球に同相です。
ここで準備のできていない人にとって最大の難しさは、「次元3の多様体」の概念と、「閉じた」および「接続された」という言葉で表される特性です。 したがって、ディメンション2の例を使用して、これらすべての概念とプロパティを処理しようとしますが、この場合、大幅に簡素化されます。
表面のポアンカレ予想
Mを閉じた連結面(次元2の多様体)とします。 ループを任意の場所に引っ張ってみましょう。 その場合、表面Mは2次元の球に同相です。
まず、表面とは何かを定義します。 有限の多角形のセットを取り、すべての辺(エッジ)をペアに分割します(つまり、すべての多角形のすべての辺に偶数が必要です)。各ペアで、2つの可能な接着方法のいずれかを選択します。 接着します。 その結果、閉じた表面が学習されます。
結果のサーフェスが1つのピースで構成され、複数の個別のサーフェスではない場合、それらはサーフェスが接続されていると言います。 正式な観点から見ると、これは、ポリゴンの頂点から接着した後、エッジに沿って他の頂点に移動できることを意味します。

簡単な例を示します。上の図のすべての三角形が正しいと仮定した場合、接着後、表面が球体と同相である正四面体が得られます。
正式には、接着後のポリゴンの頂点から(エッジに沿って)ポリゴンの頂点に移動できるようにする必要があります。
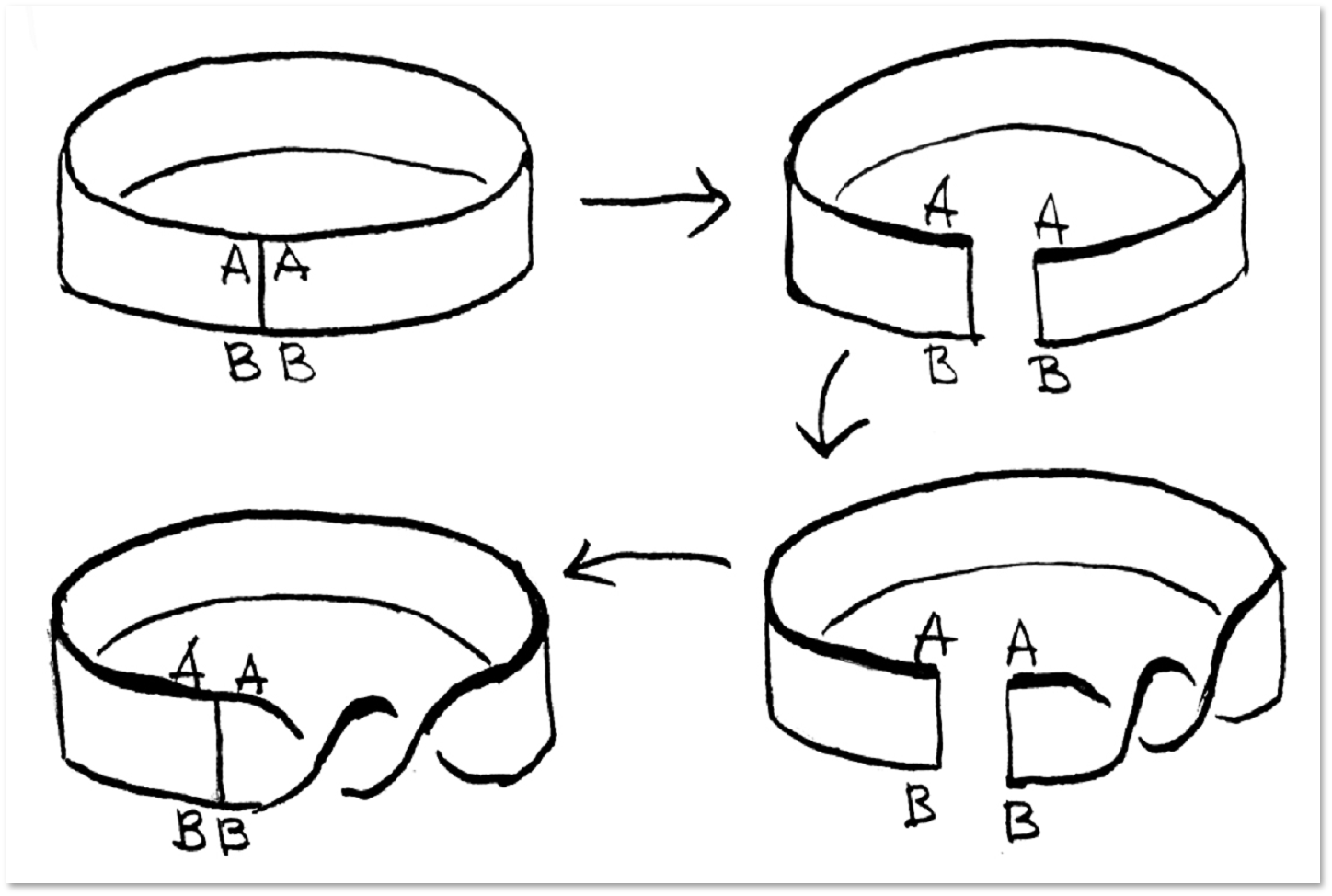
接続されたサーフェスは、1つのポリゴンから接着することもできます。 図は、これがどのように正当化されるかのアイデアを示しています。

簡単な接着剤の例を考えてみましょう。
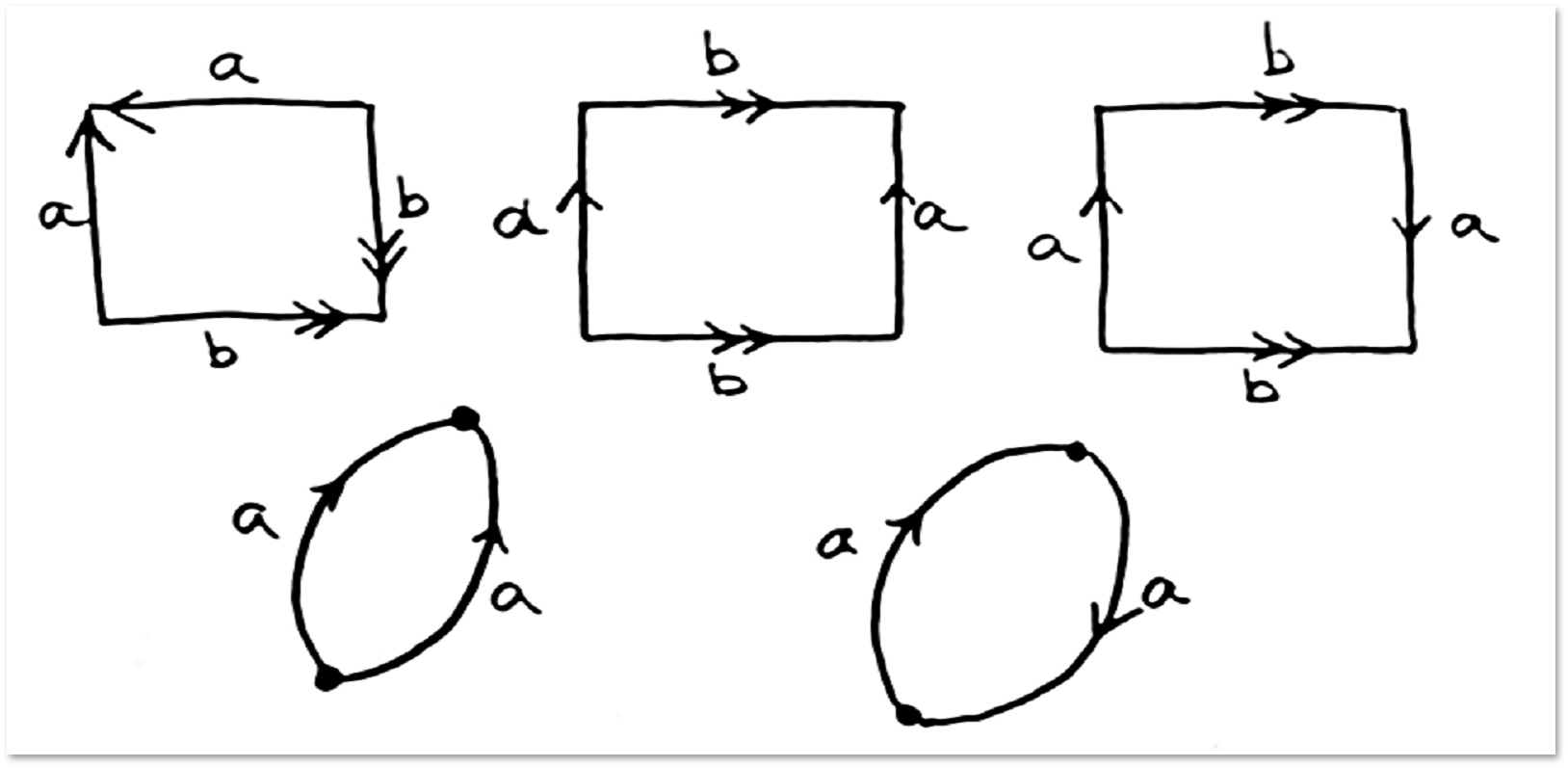
最初のケースでは、球を取得します。
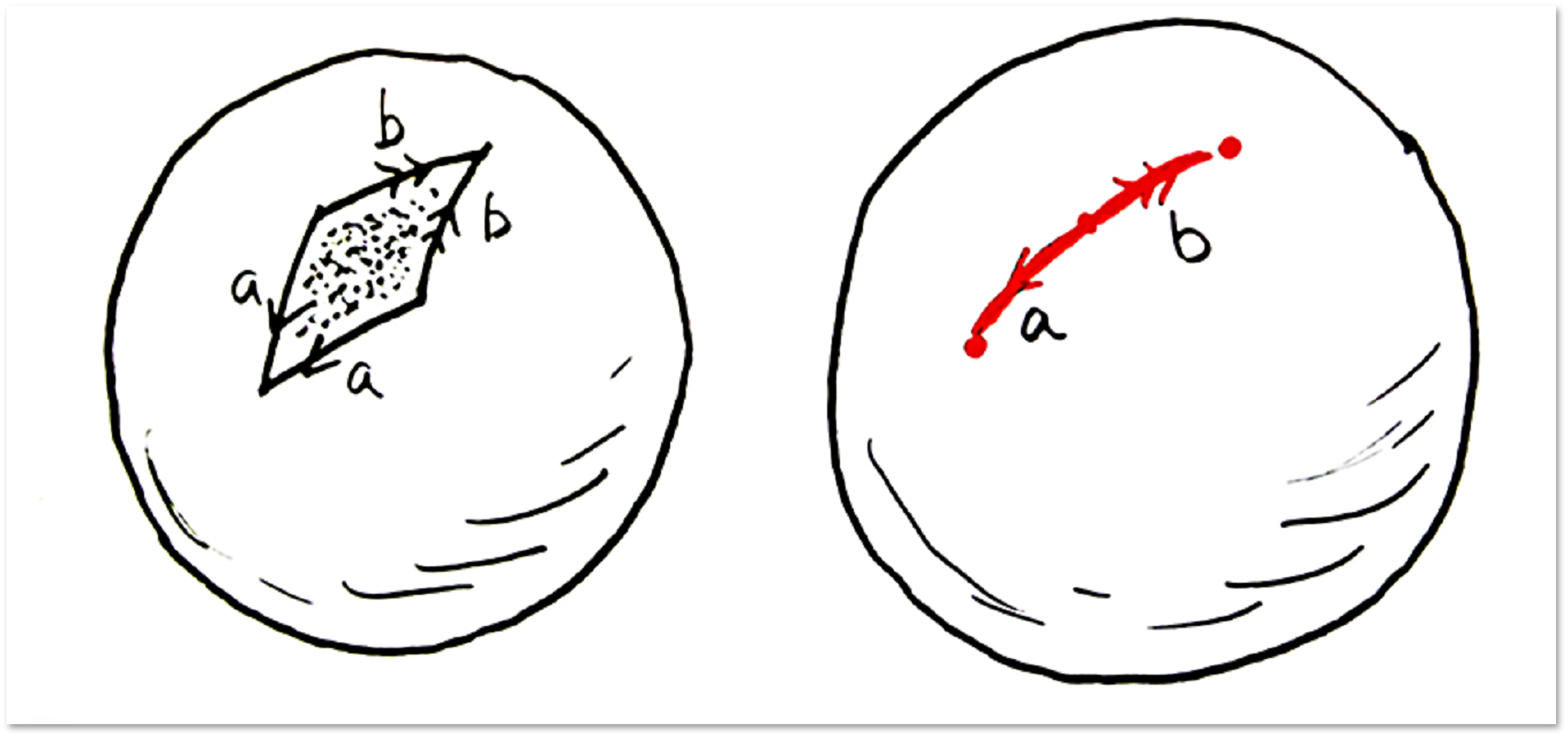
2番目のケースでは、トーラスを取得します(ドーナツサーフェス、以前に会った)。
3番目のケースでは、いわゆるクラインボトルを取得します。

ポリゴンのすべての辺が接着されていない場合、エッジのある表面が得られます。
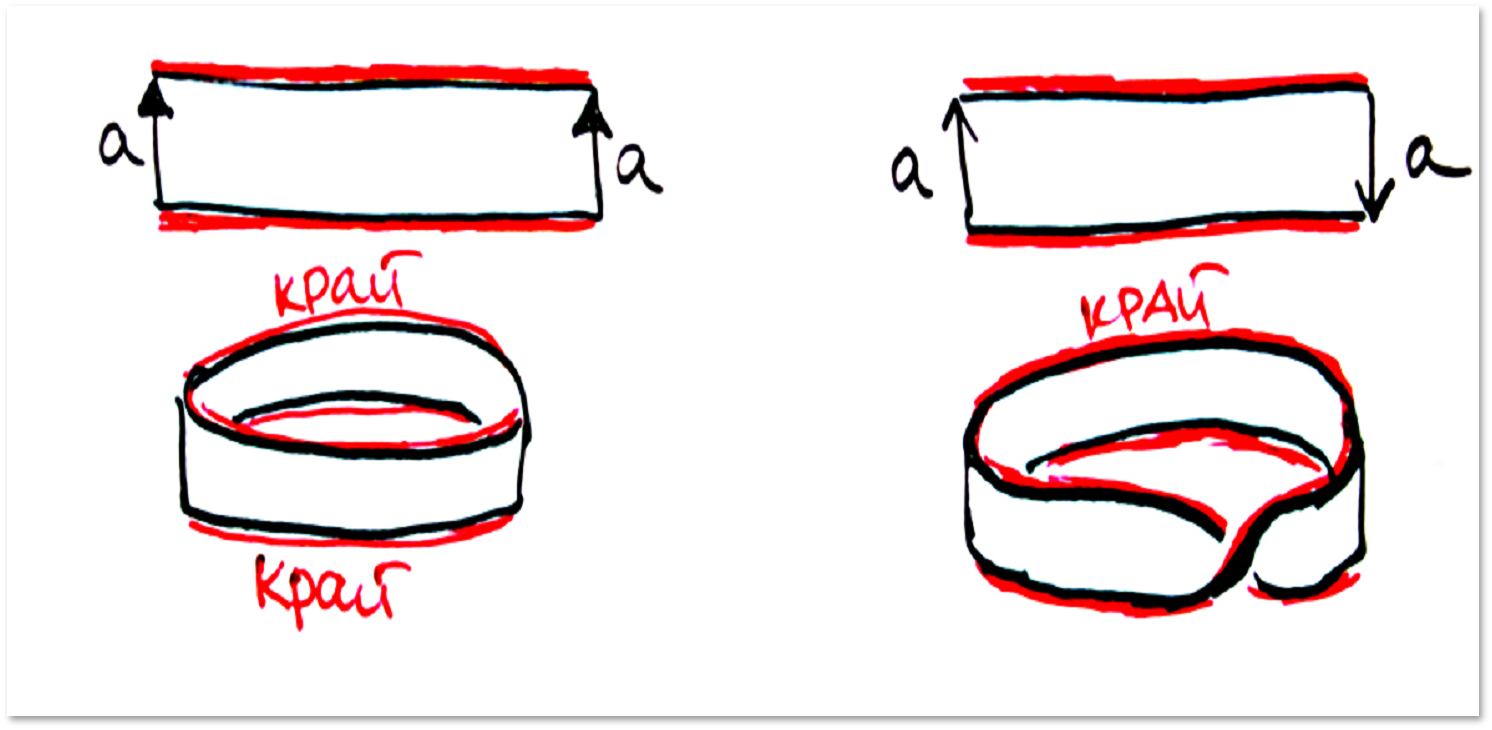
それから「傷跡」を接着した後、本質的に純粋に「化粧品」であることに注意することが重要です。 表面上のすべてのポイントは等しく、どのポイントもディスクと同相の近傍を持ちます。
2つのサーフェスは、それぞれの接着パターンが小さなポリゴンの接着パターンに切断され、接着パターンが同じになる場合、同相と見なされます。
立方体の表面を四面体のスキャンを追加できる部分に分割する例を使用して、このステートメントを分析してみましょう。
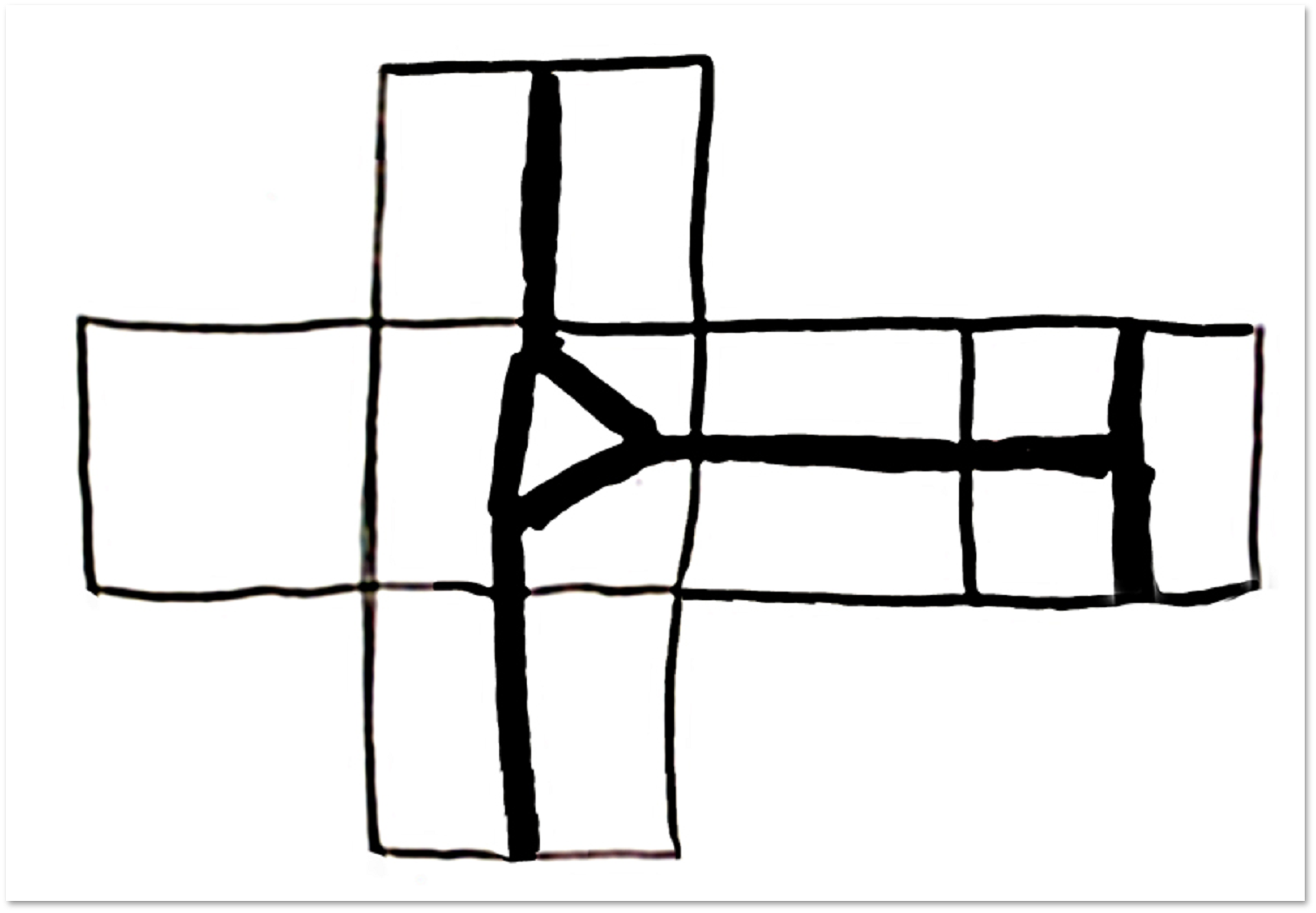
より一般的な事実も当てはまります。すべての凸多面体の表面は球体です。
それでは、ループの概念について詳しく見ていきましょう。 花弁は、検討中の表面上の閉じた曲線です。 2つのループは、片方が引き裂かれたり接着したりせずに表面に残ったまま他方に変形できる場合、ホモトピックと呼ばれます。 以下は、平面または球でループを縮小する最も単純なケースです。
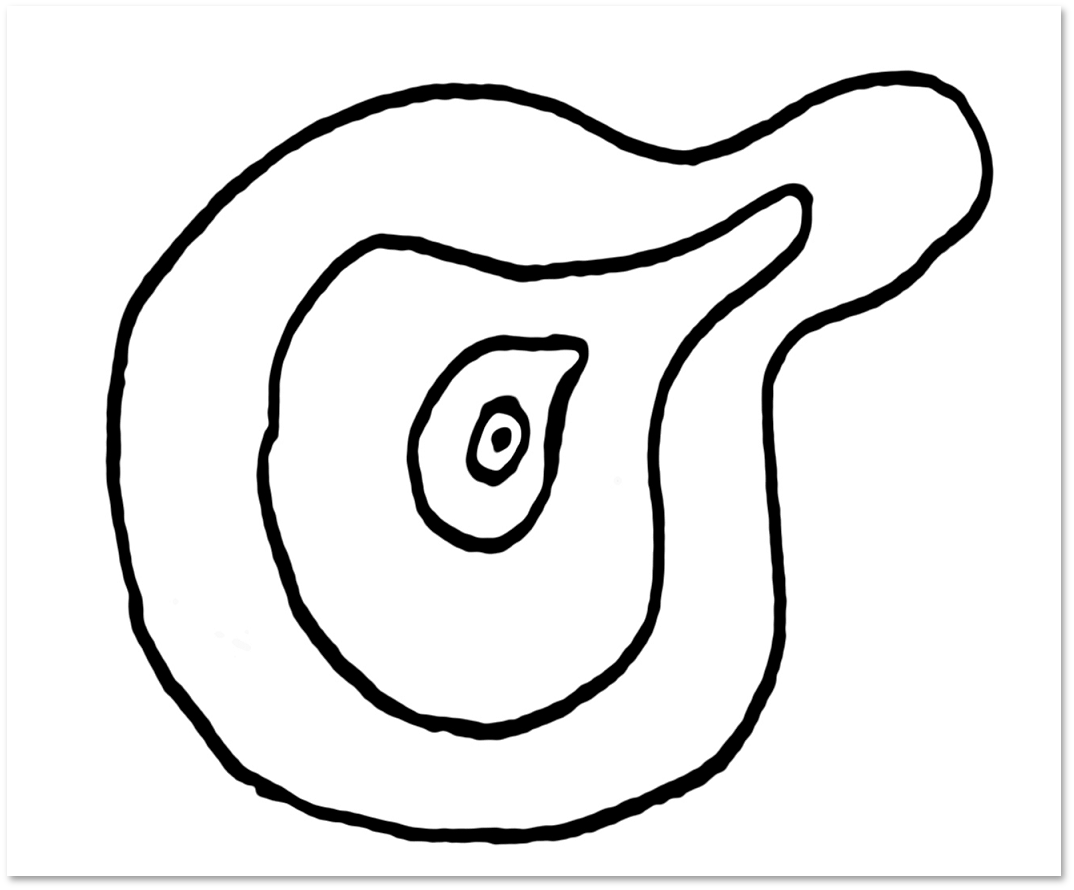
平面または球上のループに自己交差がある場合でも、一緒に引っ張ることができます。

飛行機では、ループを締めることができます。
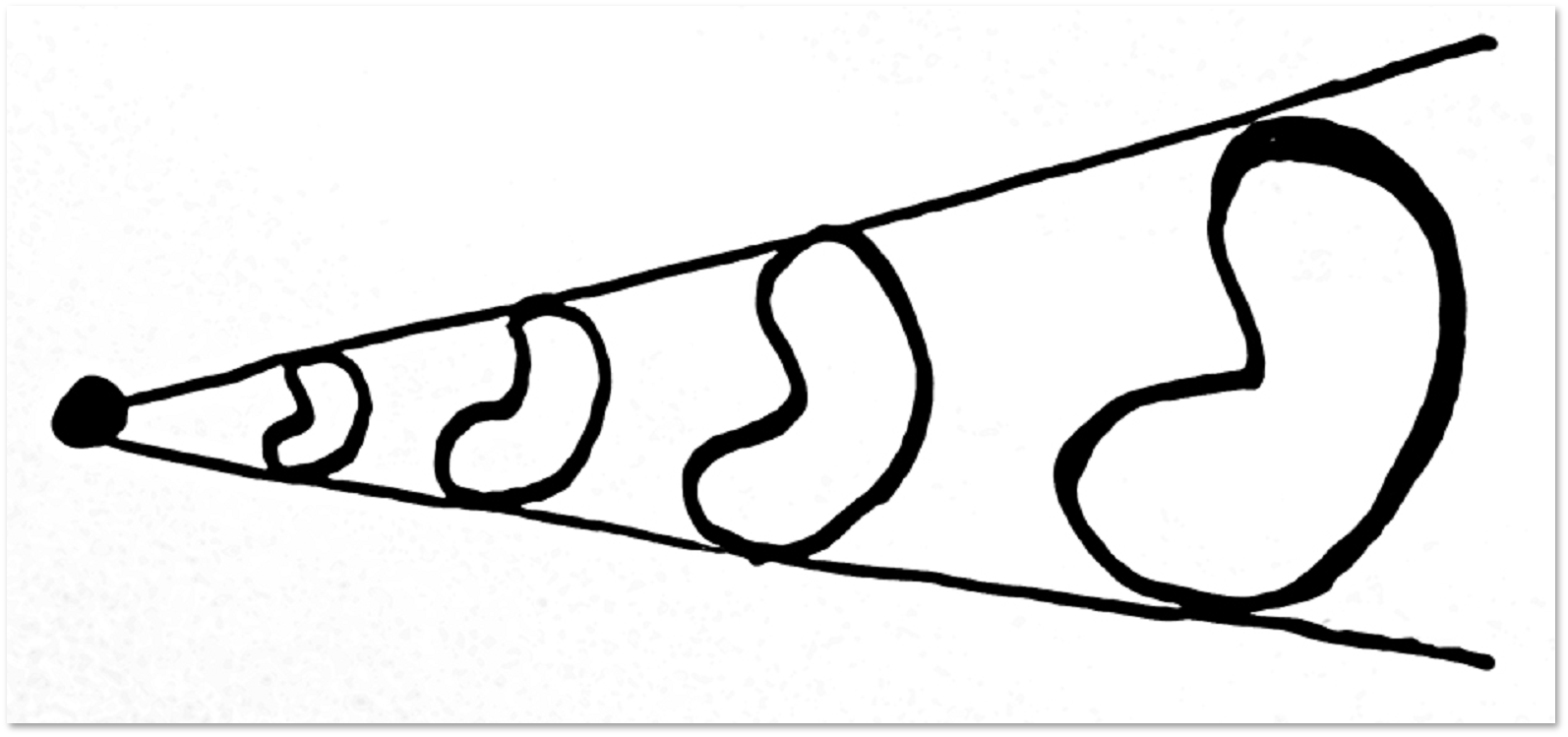
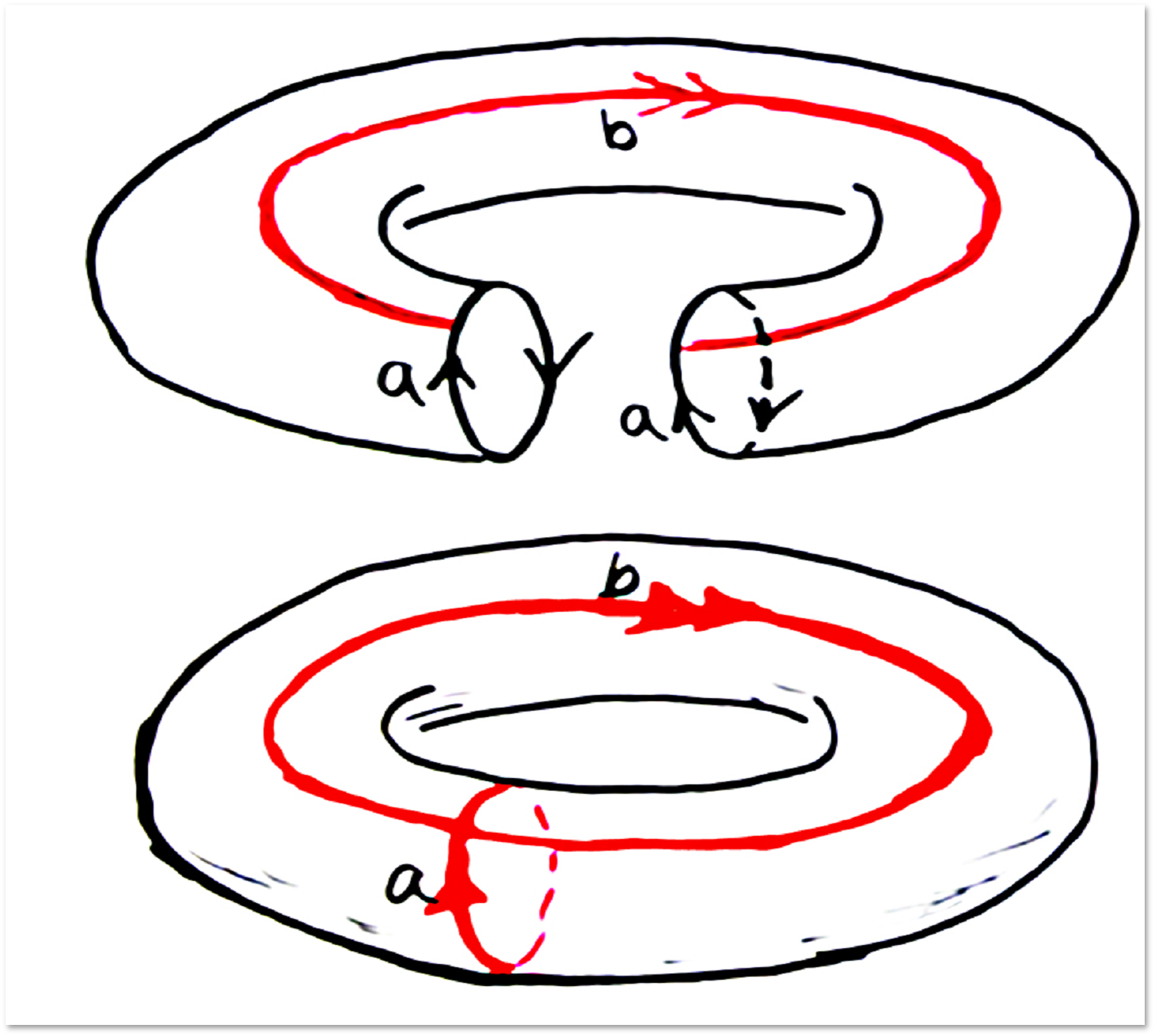
しかし、トーラス上にあるループ:
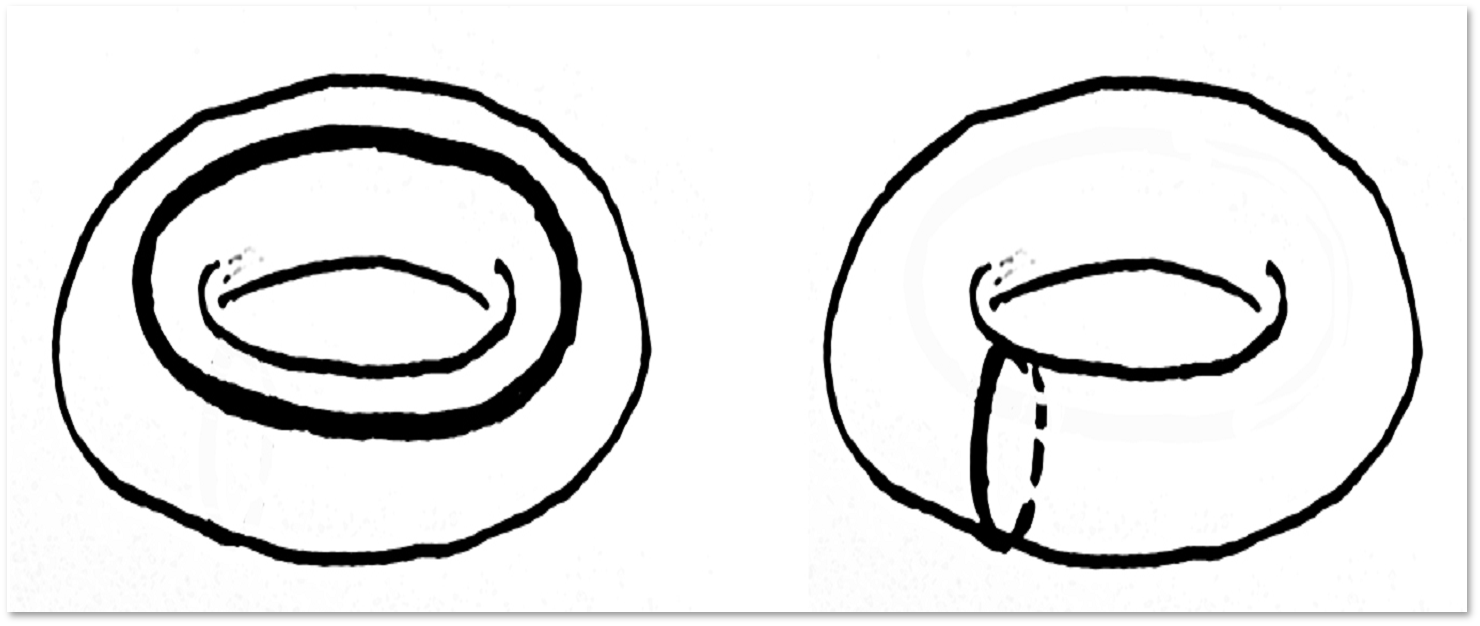
このようなループを引き締めることは不可能です。 (残念ながら、この証明は私たちの物語の範囲をはるかに超えています。)さらに、トーラスに示されているループはホモトピックではありません。 リスナーまたは読者がトーラス上で、これら2つと同種ではない別のループを見つけることをお勧めします-これは非常に単純な質問です。 その後、これら3つと同種ではないトーラス上の4番目のループを見つけてみてください-これはやや複雑になります。
オイラー特性
ポアンカレ予想の定式化からのすべての基本概念に精通したので、2次元の場合の証明を開始しようとします(もう一度、これは3次元の場合よりも何倍も簡単であることに注意してください)。 そして、オイラーの特性はこれに役立ちます。
表面Mのオイラー特性は、数B − P +Γです。 ここで、Gはポリゴンの数、Pは接着後のエッジの数(検討中のサーフェスの場合、これはすべてのポリゴンの辺の数の半分です)、Bは接着後の接着後に得られる頂点の数です。
2つの接着スキームが同相曲面を定義する場合、B – P + Pの数はこれらのスキームで同じです。つまり、B − P +は表面の不変量です。
表面がすでに何らかの形で定義されている場合、何らかの種類のグラフを描画して、表面に沿って切断した後、表面がディスクと同相の断片に分割される必要があります(たとえば、リングは禁止されます)。 次に、値B − P + Gを計算します。これは、表面のオイラー特性です。
同じオイラー特性を持つサーフェスは同相であるか、後で学習します。 しかし、表面のオイラー特性が異なる場合、表面は同相ではないと断言できます。
凸多角形の有名な関係B − P +Γ= 2(オイラーの定理)は、この定理の特別な場合です。 この場合、特定の表面-球体について話しています。 備考指定:表面Mのオイラー特性をχ(M)で表します:χ(M)= B-P +Γ
表面Mが接続されている場合、Mが球に同相である場合にのみ、χ(M)≤2、χ(M)= 2になります。
講義を最後まで見て、次元2のポアンカレ予想がどのように証明されているか、そしてグリゴリーペレルマンが次元3でそれを証明した方法を学びます。