こんにちは 最近、ケプラー方程式についての投稿がここでスリップし、それが一般的にどのように導出され、どこで、歴史的にも数学的にも書かれていないという事実に少し驚いた。 ご存知のように、ケプラーは惑星運動の観測から彼を連れ出し、ランダウとリフシッツは惑星運動を...
ラグランジュ関数がなければ、理論力学は不可能です。 私は彼女の結論を述べません。すべての塩はハミルトンの最低の行動の原則であると言うだけです、
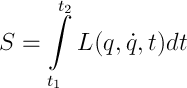
それに応じて、機械システムが移動するため、上記の積分は、ちなみにアクションと呼ばれ、可能な最小の値を持ちます。 おそらく、「関数の変化」は何かを教えてくれます-もしそうなら、それからラグランジュ方程式（UL）（1）、オイラー方程式、そこから続く自由粒子のために-これはその派生のオプションの1つです。 そうでなければ、すべてが少し悪くなります。つまり、ニュートンの第二法則を分析し、計算に約2ページを費やし、一般化された座標と力と関係の概念を導入し、最終的に同じオプションになります。 ところで、運動エネルギーとポテンシャルエネルギーの違いとして、ラグランジュ関数（PL）（2）が自然に導入されるのは2番目の方法です。
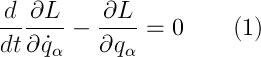
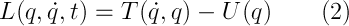
表記に関して、qは一般化された座標であり、ポイントは時間微分です。 重要！ ラグランジュ形式によれば、一般化された座標と速度は独立した量です！ 自由粒子（または閉じたシステム、つまり外力の影響を受けないシステム）の場合：
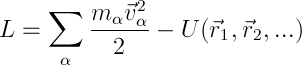
一般化された座標のインデックスは、一般に、各座標の微分方程式系であることを示しています。
簡単に反対方向に、一般化された座標を半径ベクトルと速度に置き換えます。
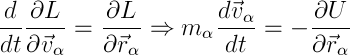
ラグランジュ方程式からニュートン方程式を取得します（時間による半径ベクトルの導関数は速度に等しいことを思い出してください）。
ここで、PLが加算的であることを追加する価値があります。つまり、システムのPLはその部分のPLの合計です。
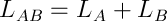
素晴らしい、基盤があります。 さて、ケプラー方程式を得るには、壁を構築する必要があります-一般化されたエネルギー、運動量、角運動量。 ここでは、実際には非常に大きく、「ネーター定理」という名前の小さな声明を作成することが重要です。少なくとも私たちが記述している身体の規模での空間です。
- 一律
- 等方性
- 時間は一定です。
したがって、3つの保存則、3つの積分積分、つまり、初期条件のみに依存して運動中に保存される値を導入できます。
一般化されたエネルギーから始めましょう。 私ができる最も明白なことはそれを手に入れることです。 つまり、時間の均一性を利用します。つまり、PLは時間に明示的に依存せず、PLの全導関数を取得し、ULを置換することで変換します。
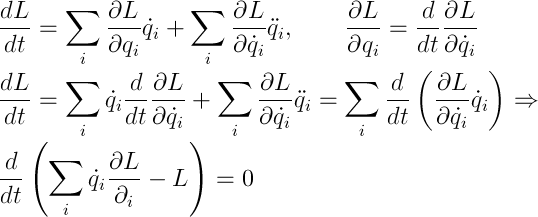
どこで
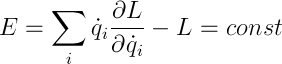
できた ところで、エネルギーが保存された機械システムは、保守的と呼ばれます。
一般化された運動量の保存は、空間の均一性、特に空間での並列システム転送の自由から得られます。 宇宙のシステムのイプシロンへの無限の転送、すなわち システムの部品の半径ベクトルは（1）のように変化します。 PLの変化は（2）として記述されます。これは、イプシロンのランダム性により、ゼロに等しい偏導関数の合計の形で書き換えることができます。 残りは単純です（3）。運動量の合計（4）は移動しても変化しないことがわかります。
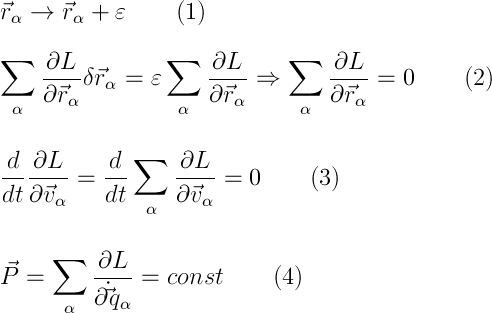
ここでは、慣性中心の概念を紹介します。 一般に、機械システムは、直線に沿って移動する点や、この点に対して何らかの形ですでに移動している他の物体の形で直感的に表現できます。 したがって、この点は慣性の中心です。つまり、総質量を持つ点の形で閉じた機械システムを表し、他のすべてをシステムの内部エネルギーに入れます。
勢いの瞬間で、それは勢いの瞬間でもあり、すべてが同じようになりますので、結果を書きます：
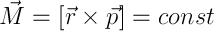
要約すると、UL、FL、および運動の3つの積分、エネルギー、運動量、角運動量があります。
最後に、私はあなたの時間を無駄にしていることに移ることができます:)それは、特定のケースでケプラー方程式が続くことから、「二体問題」と呼ばれます。 手始めに、それを簡素化します。 2つの物体のPLを記述し（1）、相互距離のベクトルを導入します（2）。 同時に、原点を慣性の中心に配置し、（3）を与えます。 2番目と3番目の方程式から、両方の点の半径ベクトルを見つけ（4）、それらを最初の（5）に代入します。 減少した質量（6）をここに紹介します。
したがって、二体問題は、いくつかの中心的な分野での一体問題に還元されます。
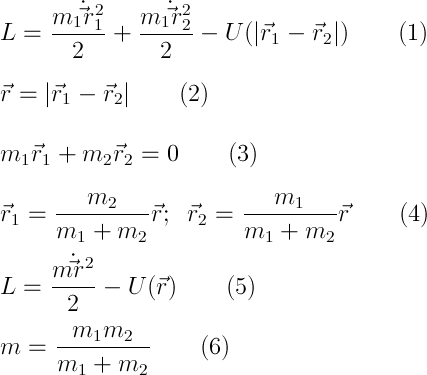
中心磁場M = [rp]の角運動量を考えます。 ここから、Mとrは垂直であり、Mの恒常性から（運動の積分、覚えていますか？）システムの半径ベクトルが常に同じ平面にあることは明らかです-平面運動があります。トートロジーの場合）およびz軸、運動平面に垂直-本質的に極性。 FLの書き換え：
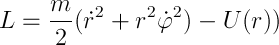
座標を見て
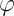-彼女はいない！ 時間微分のみがあり、これを巡回と呼ぶ権利を与え、対応する一般化された運動量が保存されると言い、問題の解決は単純化されます。 この場合、それは勢いの瞬間と一致します
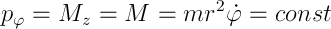
また、PLには明示的に時間は含まれません。つまり、システムのエネルギーも同時に節約されます。 一連の計算の後
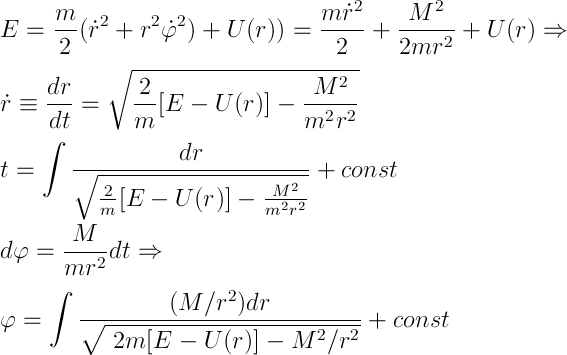
求積法、つまり積分で問題の解を得ます。 同時に、有効なポテンシャルエネルギーを導入します
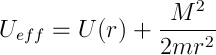
そして、ケプラー方程式はそれと何の関係があるのか、後列から質問が聞こえます。 良かった、良かった、説得された、私自身はもうすぐ...
中央のポテンシャル場を移動する問題を見てみましょう
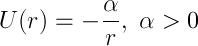
マイナス記号は引力を示します（プラス記号は反発を意味します。この場合、これは私たちにとって興味深いことではありません-粒子は反射して無限に行きます）。 このタスクには独自の名前さえあります-はい、ケプラーのタスク。 有効ポテンシャルエネルギーとそのグラフを作成します。 明らかに、rがゼロに近づくと、無限大になる傾向があり、半径ベクトルがそれぞれ無限大になるとゼロになります。
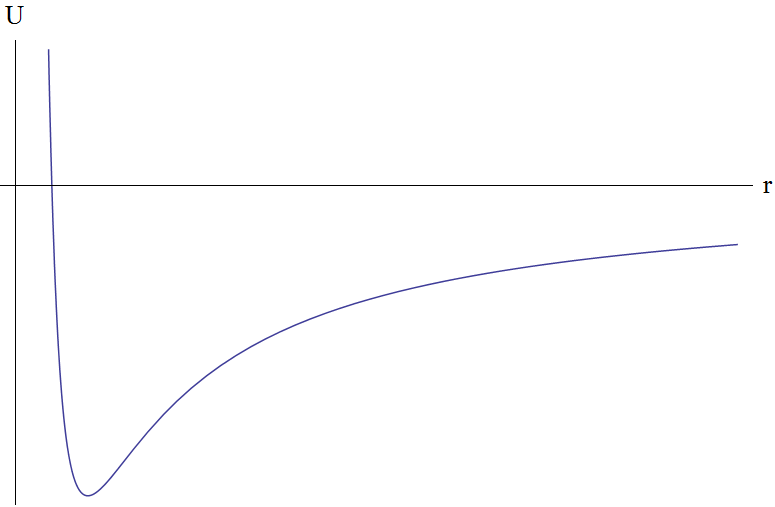
グラフから明らかなように、エネルギーE> 0の場合、運動は無限になります。つまり、粒子は無限になり、E <0の場合、有限になります。 軌道の形状は、一般式によって決定されます
ポテンシャルの形をそれに代入した後、記法のペアを導入する
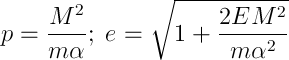
const = 0になるように、角度の原点を変換して選択します
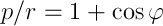
ここで、pとeはそれぞれ軌道のパラメーターと離心率です。 ケプラーの方程式です。
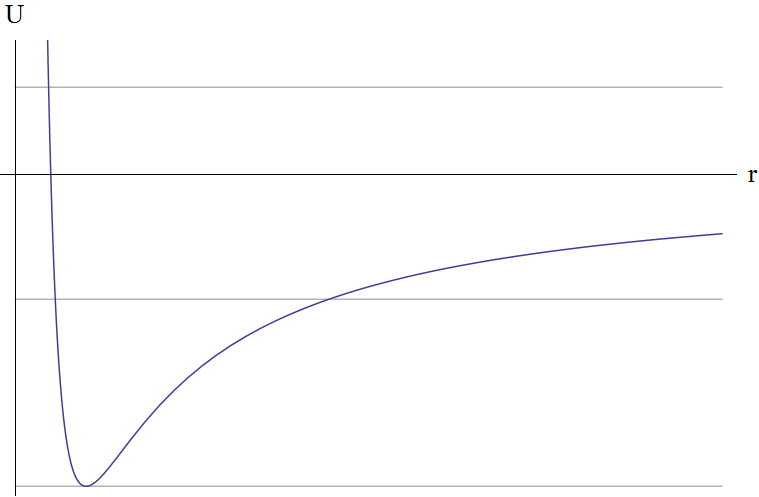
結果を分析しましょう。 これを行うには、有効ポテンシャルエネルギーのグラフをもう一度見てください。
灰色の線は、システムの可能なエネルギー値です。 つまり、もちろん、それらはすべてより小さい可能性があります
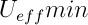しかし、これらを考慮します。 下から上：
- 最低点は最小点です。 E <0、e = 0-運動の軌跡-円。 ケースはまれであり、非常に単純です。
- もう少し高い。 E <0、0 <e <1-楕円。
運動は有限であり、楕円の長軸と短軸を次のように定義することもできます。
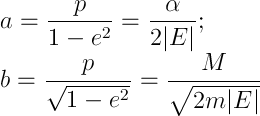
これは、解析ジオメトリの式から直接続きます（ここでは、おそらく、VygodskyまたはWikiに近いところに送ります）。 楕円、近日点、遠日点の焦点までの最小距離と最大距離
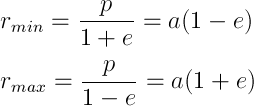
一般的に言えば、額から得ることができるもの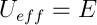
。 軌道の回転時間はケプラーの第二法則から得られます 
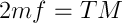。 楕円の場合、セクター速度 
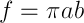、つまり
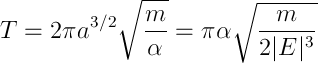
ケプラーの第三法則があります
。
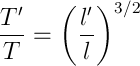ここで、周期は粒子エネルギーにのみ依存することに注意してください。
- E = 0、e = 1。 軌道は無限です、それは放物線です
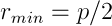。 そのような軌道は、静止状態から無限遠から移動する粒子に対するものです。
- E> 0、e> 1。 軌道は再び無限ですが、今回は近日点を伴う双曲線です
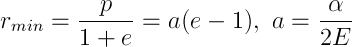
おそらく、これがメカニズムの基本的な問題の1つについてお話ししたいことのすべてです。 ケプラー問題は、非常によく研究されているが簡単な数学的モデリングシステムのテストによく使用されます。 調和振動子の問題とともに、これは、物体が同じ速度で開始点に戻るときの、閉じた経路に沿った物体の動きに関する2つの問題の1つです。 ケプラー問題は、古典的な力学の新しい方法、特にハミルトニアン形式、ハミルトン-ヤコビ方程式、および作用角変数システムを構築するために使用されます。