約1年前、別の世界があることがわかったときにすべてが変わりました。 世界はあなたと私たちのものとは異なります。 よりクリーンで予測可能な世界。 副作用、突然変異、配列、破壊的な更新(変数への再割り当て)のない世界。 執念の最も賢い女王が彼女と彼女の美しい姉妹を支配する世界-機能と再帰。 私は、ほぼすべての既知のデータ構造の投影が調和して存在する、または実際に存在する、純粋に機能的な世界について話している。
そして今、私はあなたにこの世界の小さな粒子を見せたいです。 鍵穴を通して、この素晴らしい世界を一瞬見て、その最も印象的な住民の1つである機能的な赤黒木(CPD)を調べます。
純粋に機能的なデータ構造について
クラスとしての純粋に機能的なデータ構造(CFSD)には、2つの理由があります。 まず、99%の命令型実装では、いわゆる破壊的な更新が障害(以前の値が失われた変数への割り当て)です。 機能的な世界でこのようなシナリオが不可能であることは明らかです。なぜなら、私たちは常に不変のオブジェクトを扱うからです。 第二に、機能的な世界では、コレクションを変更した後、以前のバージョンが引き続き利用できることを期待しています。 したがって、「永続オブジェクト」という用語-オブジェクトの複数のバージョンのサポート。
したがって、よく知られた命令的実現を機能的な世界に単純に取り入れて移植することはできません。 その制限(更新なし)と要件(永続性)を覚えておく必要があります。 したがって、命令型実装を機能的環境に適合させるプロセスは、やや複雑であり、神秘的ですらあります。 そして、 Chris Okasakiの基本的な仕事-Purely Functional Data Structuresは、15年間、この困難な問題で卓越したマスターと見なされてきました。
クリスと彼の本について
1998年、ChrisはCFPSのテーマに関する論文を擁護し、1年後に本の形で論文を発表しました。 クリスの本は、200ページの非常に密集した(有益な)魅力的な読書です。 テキストは、科学的な仕事とバーでの友人との非公式の会話の境界をなすスタイルで、文字通り芸術小説のように読みます。 Chrisの研究は、CFSDの実装におけるベストプラクティスとアプローチを組み合わせており、Standard MLとHaskellのよく知られている(そうではない)データ構造の例によってサポートされています。
2つのキーについて
注意深い読者は、そのような要件と制限があると、すべてがひどく遅くなると言うでしょう。 機能コレクションの変更には、永続性を維持するための完全なコピーが伴うようです。 これは完全に真実ではありません。 もっと正確に言えば、まったくそうではありません。 コピーは実際に存在しますが、最小規模です。 より正式に-本当に変化しているものだけがコピーされます。 コレクションの残りは(より大きなルールとして)バージョン間で共有されます。 これら2つの文は、純粋に機能的なデータ構造を理解するための鍵です。 これらは、FPの鋭い頭脳によって発明され完成されたユニークなツールです。 これらのツールの名前は、パスコピー(操作の影響を受けるもののみをコピーする)および構造共有(共通部分はバージョン間で安全に共有できます。このような各部分自体は不変です)。
二分探索木について
まず、通常の不均衡なバイナリ検索ツリー(DBP)を検討します。これは、機能的な世界に非常に簡単に移植できます。 その構造は次のようになります。
abstract sealed class Tree { def value: Int def left: Tree def right: Tree def isEmpty: Boolean } case object Leaf extends Tree { def value: Int = fail("Empty tree.") def left: Tree = fail("Empty tree.") def right: Tree = fail("Empty tree.") def isEmpty: Boolean = true } case class Branch(value: Int, left: Tree = Leaf, right: Tree = Leaf) extends Tree { def isEmpty: Boolean = false }
貼り付け操作に興味があります。これにより、パスコピーおよび構造共有ツールの強さと美しさを十分に理解できます。
def add(x: Int): Tree = if (isEmpty) Branch(x) else if (x < value) Branch(value, left.add(x), right) else if (x > value) Branch(value, left, right.add(x)) else this
命令型アルゴリズムと同様に、挿入タスクは、新しいノードに適した場所を見つけるタスクに削減されます。 ただし、機能的な実装はもう少し興味深いものになります。 機能ツリーに挿入する操作は、
add
呼び出しのトップダウンチェーン(挿入する場所を検索する)とブランチコンストラクターの呼び出しの昇順(ボトムアップ)チェーン(検索パスに沿ってツリーの変更された部分をコピーする)の2つのパスを組み合わせます。 最初のパス(挿入ポイントのトップダウン検索)は、命令型アルゴリズムの明らかな投影です。 実装を完全に機能させる(永続的な)2番目のパス(上流パスのコピー)に興味があります。
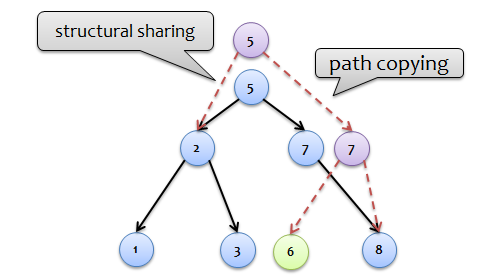
永続プロパティを保持するには、コレクションの2つのバージョン(「前」と「後」の挿入)をサポートする必要があります。 したがって、ノードの内部構造の変更は、そのコピーに対して実行する必要があります。 ツリーへの挿入の結果として、ノード更新(左/右の子孫へのリンクの変更)の一種の「連鎖反応」が発生し、検索ポイントに沿って挿入ポイントからツリーのルートに広がります。 これは、アイデアとパスコピー(ノード「5」と「7」がコピーされる)と構造共有(「1」、「2」、「3」のキーを持つサブツリー)を組み合わせて、上向きのパッセージが実装する「魔法」を説明する方法ですコレクションの両方のバージョンに含まれています)。
赤黒木について
赤黒木(QCD)は、2つの不変式が有効な自己バランス型バイナリ検索ツリーです。
- 赤の不変式 :赤のノードに赤の祖先がない
- 黒の不変量 :ルートから葉への各パスには同じ数の黒ノードがあります
これらの不変条件が満たされると、ツリーはlog nの高さとバランスが取れます。ここで、nはツリー内のノードの数です。 つまり、PSPの主な操作は対数時間で実行されることが保証されています。
1999年まで、機能的な世界ではQCDの問題はありませんでした。 命令型実装は、ポインターを使用した複雑な操作(ポインター地獄)で完全に構築されているため、移植が難しいことで有名です。 したがって、たとえば、コーメンは、不変条件の違反の8つの可能性のあるケースと、それらを排除するための対応する手段を調査しました。 トピックからわずかに逸脱して、CPhがあらゆる可能な方法で代替物に置き換えるために試みた過度の複雑さのためであると付け加えることができます。 たとえば、SejevikはLLRBツリーをQCDの簡易バージョンとして提案しました 。
しかし、1999年に、Chris OkasakiはQCDの純粋に機能的な実装を紹介した記事を公開しました 。 この記事は、機能的プログラマーと命令型プログラマーの両方から大きな需要があります。 実際、この記事では、プログラマが15分で理解してプログラミングできる、非常にシンプルで理解しやすい実装のアイデアを紹介しています。 クリスは、不変条件の1つに違反するパターンは4つしかないと言いました(下図を参照)。 そして、私たちのタスクは、これらのパターンを見つけて、赤いルートと2つの黒い子を持つ同じデザインに再構築することです(図を参照)。 そしてそれだけです。 つまり DBPからPSDを取得するには、挿入アルゴリズムの2番目(上流)のパスを変更するだけです。 2番目のパスでは、検索パスに沿ってノードをコピーするだけでなく、サブツリーが4つのパターンのいずれかに一致する場合、安全な構造に再構築する必要があります。 つまり、アルゴリズムのコピーフェーズは、バランシングフェーズと組み合わされます。
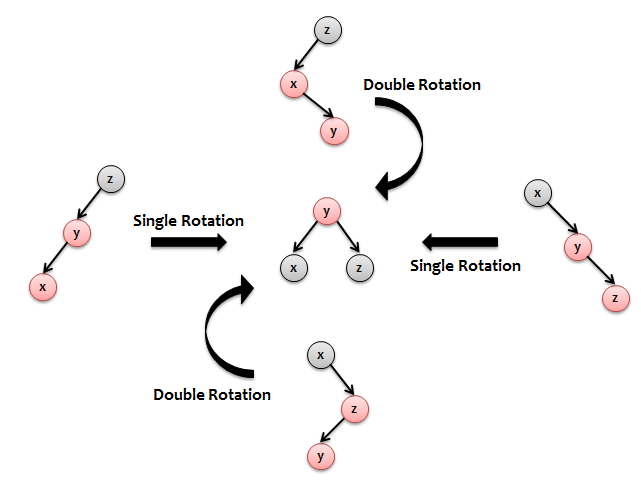
PSDのルートが常に黒であり、新しいノードが常に赤であるという2つの単純な事実に加えて、次のコードを取得します。
def add(x: Int): Tree = { def balancedAdd(t: Tree): Tree = if (t.isEmpty) Tree.make(Red, x) else if (x < t.value) balanceLeft(t.color, t.value, balancedAdd(t.left), t.right) else if (x > t.value) balanceRight(t.color, t.value, t.left, balancedAdd(t.right)) else t def balanceLeft(c: Color, x: Int, l: Tree, r: Tree) = (c, l, r) match { case (Black, Branch(Red, y, Branch(Red, z, a, b), c), d) => Tree.make(Red, y, Tree.make(Black, z, a, b), Tree.make(Black, x, c, d)) case (Black, Branch(Red, z, a, Branch(Red, y, b, c)), d) => Tree.make(Red, y, Tree.make(Black, z, a, b), Tree.make(Black, x, c, d)) case _ => Tree.make(c, x, l, r) } def balanceRight(c: Color, x: A, l: Tree, r: Tree) = (c, l, r) match { case (Black, a, Branch(Red, y, b, Branch(Red, z, c, d))) => Tree.make(Red, y, Tree.make(Black, x, a, b), Tree.make(Black, z, c, d)) case (Black, a, Branch(Red, z, Branch(Red, y, b, c), d)) => Tree.make(Red, y, Tree.make(Black, x, a, b), Tree.make(Black, z, c, d)) case _ => Tree.make(c, x, l, r) } def blacken(t: Tree) = Tree.make(Black, t.value, t.left, t.right) blacken(balancedAdd(this)) }
考慮された実装では、追加のコメントを必要とするいくつかのポイントがあります。 まず、各ツリーノードには追加情報が含まれています-それ自身の色(
color
関数)。 第二に、
balance
とコピーを実装する
balance
関数は2つの関数(
balanceLeft
と
balanceRight
)に分割され、左または右のサブツリー(検索パッチに沿ってのみ)で不変式の違反を検出し、それぞれの側で2つのパターンを処理します。
命令型実装の複雑さについて
公正な疑問が生じます。なぜ命令型の世界でのQCDの実装はもっと複雑に見えるのでしょうか? 答えは非常に簡単です-パフォーマンスが原因です。 ポインターと可変変数を処理する必要があるため、(特定の条件下で)最も早い反復でバランス調整プロセスを停止し、それによりアルゴリズムの時間を短縮できます。 機能環境では、影響を受けるすべてのノードを強制的にコピーする必要があるため、サブツリー内のパターンの存在を不必要にチェックしてもそれほど気になりません。 公平のために、機能QCDに挿入するために提案されたアルゴリズムは、命令型の世界からの元のアルゴリズムと同じ漸近的な複雑さ-O(log n)を持っていることを置き換える価値があります。
次のステップについて
このトピックに興味のある人のための素晴らしいリンクをまとめました。
研究者向け:
- Scalaの例とCFSDのレビュープレゼンテーション (ノボシビルスクScalaミーティングのビデオレポートはこちら )
- バイナリヒープを機能的な世界に移植しようとする私の試み
- GitHubのQCDおよびその他の構造のコード
- Matt MaytによるPSDからの削除
- クリス岡崎のブログ
実務者向け:
- この記事の Anre Andersoninは、比較回数を「2 * d」から「d + 1」に減らすことを提案しました。dはツリーの深さ(検索パスの長さ)です。 比較が少なくなるように、DBPの挿入操作を変更します。
- ソート済みリストからバランスの取れたDBPを作成する関数
fromOrderedList
を作成します。 ヒント:ヒンズ、ラルフ。 1999「赤黒の木の建設」。