
Japanese Crosswordは、答えが絵になる有名なパズルです。 それは何であり、それを解決する方法は、 ウィキペディアで読むことができます。 列挙を通じてWolfram Mathematicaシステムで日本語のクロスワードパズルを解くプログラムをどのように作成できるかを示したいと思います。
主なアイデア
ブルートフォースソリューションのアイデアは、すべての行と列のすべての可能なセル位置のリストを作成することです。 その後、取得したリストを使用して、情報が正確にわかるセルを見つけます。 次に、見つかった情報と矛盾するような場所を取り除きます。 直観的に、最後の2つの手順を周期的に繰り返すと、任意のセルに関する情報を見つけることができます。 そのため、タスクは3つのサブタスクに分割できます。
- すべての可能な場所の編集。
- 塗りつぶされたセルと未塗りのセルを検索します。
- 競合する場所を削除します。
Wolfram Mathematicaはリストを操作するために作成されたため、セルの位置はリストとしてプログラムに保存されます。 次のようにセルに関する情報を示します。
- 1-塗りつぶされたセル。
- 0-塗りつぶされていないセル。
- *-何も知られていないセル。
たとえば、以下は同等のリストとセルの配置を示しています。
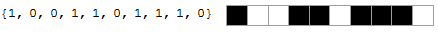
すべての可能な場所の編集
理論のビット
特定の例を考えてみましょう。 そのようなデータのあらゆる種類の場所を見つける必要があります。

これらの場所の1つを上に示します。 すべての可能な場所をソートする方法は?
次の方法でやってみましょう。 次のセルのグループをキー (フィールドの左側の数字)に割り当てましょう:
{{1,0}, {1,1,0}, {1,1,1}}
。 次に、これらのグループを順番に並べる場所を保存するリストを作成します。 これらのグループを配置する場所には、ゼロを格納します。 したがって、場所のリスト
{0,0,0,0,0}
を取得します。 セルのグループを取得した場所に必ず順番に配置すると、タスクからデータに必要なすべての配置を取得したことを簡単に確認できます。 番号が1、3、4の場所にグループを順番に配置すると、上記の例から配置が得られます。 したがって、すべての場所は、グループの数の場所の数の組み合わせと同等であることがわかります。 グループを配置する場所を何らかの方法で選択すると、可能な場所の1つが得られます。 この例のデータの場合、場所の数は10です。
「最後のグループの最後にゼロがないのはなぜですか?」および「なぜ正確に5席あるのですか?」という質問に対して、意識のある読者は答えなければなりません。
実装
Mathematicaにはこれを行う組み込み関数
Subsets[list, {n}]
があるため、列挙する関数自体を記述することを特に望んでいないことは明らかです。 リスト
list
を要素のセットとして、数値
n
をパラメーターとして取り、長さ
n
セット
list
サブセットのリストを返します。 この例では、これを使用してすべての場所を反復処理すると、次のようになります。
In := Subsets[{1,2,3,4,5}, {3}]
Out = {{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}}
次に、独自の関数を作成します。この関数は、数値(
len
フィールドの長さ、たとえばdata-
10
)とリスト(
clue
キー、たとえば
{1,2,3}
)をパラメーターとして取り、すべての可能な場所のリストを返します。 すべてを順番に行います。 最初に、数値を単位のリストに変換する関数を作成します。 組み込み関数
ConstantArray[c, n]
ます。
c
はリストに入力する要素で、
n
はこのリストの長さです。
In := ConstantArray[1, 2]
Out = {1, 1}
次に、このリストの最後にゼロを追加する必要があります。 これは
Append[expr, elem]
を使用して行われ
Append[expr, elem]
。 最初のパラメーターはリストで、2番目は添付するものです。
In := Append[{1, 1}, 0]
Out = {1, 1, 0}
純粋な関数などのオブジェクトを使用して、これら2つの関数を1つにまとめます。 これは2つの方法で行うことができます:
Function[arg, Append[ConstantArray[1, arg], 0]
またはそれより短い
Append[ConstantArray[1, #], 0]&
。
これで、キーに対応するリストの各要素にこの関数を適用できます。 これには非常に便利な
Map[f, expr]
関数があります。 関数
f
を
expr
リストの各要素に適用します。 また、
f /@ expr
という短いオプションもあります。
In := Append[ConstantArray[1, #], 0]& /@ {1, 2, 3}
Out = {{1,0}, {1,1,0}, {1,1,1,0}}
最後のグループからゼロを削除するためだけに残ります。 ここでは、
Delete[expr, {i, j}]
関数が役立ちます。 インデックス
{i, j}
持つ
expr
リストからアイテムを削除します。 最後の要素のインデックスが-1であることを忘れないでください。
In := Delete[{{1,0}, {1,1,0}, {1,1,1,0}}, {-1, -1}]
Out = {{1,0}, {1,1,0}, {1,1,1}}
収集されたものはすべて次のようになります。
In := groups = Delete[Append[ConstantArray[1, #], 0]& /@ clue, {-1, -1}]
Out = {{1,0}, {1,1,0}, {1,1,1}}
場所のリストについてはすべて明らかですが、リストlistの要素を要約する
Total[list]
関数が必要になり
list
。
In := positions = ConstantArray[0, len - Total[clue] + 1]
Out = {0,0,0,0,0}
ここで最も重要なことは、
Subsets
関数を使用することです。 さらに、リスト
{1, 2, ..., n}
を返す
Range[n]
関数と、リストの長さを与える
Length[list]
です。
In := sub = Subsets[Range[len - Total[clue] + 1], {Length[clue]}]
Out = {{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}}
セルのグループを配置する場所のリストを取得しました。 ここで、取り決めを扱います。 これを行うには、
ReplacePart[expr, i->new]
関数が必要です。この関数は、
expr
リストの番号
i
要素を
new
要素に置き換えます。 ただし、最初に置換のリストを取得するため、後でコードを記述する方が便利です。
MapThread[f, {a
関数
MapThread[f, {a
1
, a
2
, ...}, {b
1
, b
2
, ...}]
は
, ...}]
これを行うのに役立ちます。 その実装の結果は次のようになります:
{f[a
1
, b
1
], f[a
2
, b
2
], ...}
。 そのため、置換のリストを作成します。
In := rep = MapThread[Function[{x, y}, x->y], {#, groups}]& /@ sub
Out = {{1->{1,0}, 2->{1,1,0}, 3->{1,1,1}}, {1->{1,0}, 2->{1,1,0}, 4->{1,1,1}}, {1->{1,0}, 2->{1,1,0}, 5->{1,1,1}}, {1->{1,0}, 3->{1,1,0}, 4->{1,1,1}}, {1->{1,0}, 3->{1,1,0}, 5->{1,1,1}}, {1->{1,0}, 4->{1,1,0}, 5->{1,1,1}}, {2->{1,0}, 3->{1,1,0}, 4->{1,1,1}}, {2->{1,0}, 3->{1,1,0}, 5->{1,1,1}}, {2->{1,0}, 4->{1,1,0}, 5->{1,1,1}}, {3->{1,0}, 4->{1,1,0}, 5->{1,1,1}}}
事業全体のフィナーレは、その代わりの取り決めです。 ここでは、余分な角かっこを削除する
Flatten[list]
を実行します。
In := all = Flatten[ReplacePart[positions, #]]& /@ rep
Out = {{1,0,1,1,0,1,1,1,0,0}, {1,0,1,1,0,0,1,1,1,0}, {1,0,1,1,0,0,0,1,1,1}, {1,0,0,1,1,0,1,1,1,0}, {1,0,0,1,1,0,0,1,1,1}, {1,0,0,0,1,1,0,1,1,1}, {0,1,0,1,1,0,1,1,1,0}, {0,1,0,1,1,0,0,1,1,1}, {0,1,0,0,1,1,0,1,1,1}, {0,0,1,0,1,1,0,1,1,1}}
それだけです。すべての星座を受け取ります。 利便性のためにこれらすべてを1つのモジュールに結合することは残り、必要な機能を取得します。
allPositions[len_, clue_] :=
Module[{groups, positions, sub, rep, all},
groups = Delete[Append[ConstantArray[1, #], 0]& /@ clue, {-1, -1}];
positions = ConstantArray[0, len - Total[clue] + 1];
sub = Subsets[Range[len - Total[clue] + 1], {Length[clue]}];
rep = MapThread[Function[{x, y}, x->y], {#, groups}]& /@ sub;
all = Flatten[ReplacePart[positions, #]]& /@ rep;
Return[all];]
塗りつぶされたセルと塗りつぶされていないセルを検索する
ここで、関数を使用して得られるこのすべての利点の中で、セルに関する情報を抽出する必要があります。 場所のリストがあるとします。 すべての場所に1または0が存在する場所がある場合、これにより、この位置には常に塗りつぶされたセルまたは塗りつぶされていないセルがあると断言する権利が与えられます。 私の意見では、これを行う関数の最も簡単な実装は次のとおりです。すべての場所は要素ごとに合計され、すべての場所の数に等しい数またはゼロが結果リストで検索されます。 前者の場合、これらの数値は単位に変わり、後者の場合、ゼロはそれぞれの場所に残ります。 他のすべての要素はアスタリスクに置き換えられます。 実装には、
ReplaceAll[list, rule]
関数を使用します。
list
内のアイテムをルールに置き換えます。
x_ /; x!=0
構築し
x_ /; x!=0
x_ /; x!=0
は、「
x ≠ 0
ある要素
x
」を意味します。
findInformation[list_] := ReplaceAll[Total[list], {x_ /; x!=0 && x!=Length[list] -> "*", x_ /; x==Length[list] -> 1}]
この例では、関数は次のように機能します。
In := findInformation[allPositions[len, clue]]
Out = {*,*,*,*,*,*,*,1,*,*}
すべての場所の8番目のセルは網掛けされているため、グリッド全体では網掛けされています。 他の細胞については何も言えません。
競合する場所を削除する
取得した情報は、矛盾する場所を除外するために使用できます。
DeleteCases[expr, pattern]
関数がフィルターになります
DeleteCases[expr, pattern]
リストから
pattern
一致しないすべての要素を削除し
pattern
。
Except[c]
関数も使用されます。この関数は、パラメーターを除くすべてを選択します。
deleteFromList[list_, test_] := DeleteCases[list, Except[ReplaceAll[test, "*"->_]]]
例に戻って、セルの配置が
{*,*,0,0,*,1,0,*,*,*}
ようなパターンを満たさなければならないことを取得しましょう。 関数を実行すると、次のものが得られます。
In := deleteFromList[allPositions[len, clue], {"*","*",0,0,"*",1,0,"*","*","*"}]
Out = {{1,0,0,0,1,1,0,1,1,1}, {0,1,0,0,1,1,0,1,1,1}}
10か所のうち、パターンを満たすのは2か所だけであることが判明しました。
すべてをまとめる。 最終段階
クロスワードパズルを段階的に解決するために必要なすべての関数を作成しました。 今では、解決策を得るためにすべてを美しく収集することが重要です。 例として、私は日本のクロスワード「Relax」のキエフ雑誌から取られたクロスワードパズルを使用しています。 著者はA. Leutaです。
クロスワードパズルは、行と列のキーのリストの形式でプログラムに設定されます。
rows = {{1}, {2}, {4}, {3,1}, {4,1}, {12}, {9}, {4,1}, {1,1,1,1,1}, {1,1,1,1}, {1,3,1}, {2,1,1}, {9,1}, {4,5,1}, {3,4,1}, {3,5,3}, {3,1,5}, {5,1,2}, {7,3}, {4,10}, {4,3,3}, {4,2,3}, {5,2,2}, {5,3,2}, {4,1,1,2}, {3,2,2}, {2,2}, {7}, {10}, {2,6}};
cols = {{3}, {6}, {8}, {13}, {1,12,1}, {2,7,2,1}, {5,2,7,4}, {5,3,12}, {8,2,3,1,1,2}, {8,2,1,3}, {2,3,4,1,4}, {2,2,1,1,5,3,5}, {4,6,7,2}, {2,3,3,8,2}, {1,2,2,2}, {1,4,1}, {2}, {2}, {9}, {1}};
とにかくグリッドサイズを定義できるため、グリッドサイズを入力する必要はありません。
rowlength = Length[cols]
collength = Length[rows]
プログラムでは、図面はリストのリストまたは通常のマトリックスとして保存されます。 決定前は情報がまったくないため、その各要素はアスタリスクになります。
pic = ConstantArray["*", {collength, rowlength}];
クロスワードパズルソリューションの最も扱いにくい部分は、あらゆる種類の場所のリストに記入することです。 ここで少し待つ必要があります。
rowpos = allPositions[rowlength, #]& /@ rows;
colpos = allPositions[collength, #]& /@ cols;
すべての場所がいっぱいになったら、決定を進めることができます。 アイデアは次のとおりです。検索は塗りつぶされたセルのすべての行で実行され、これらのセルはメイングリッドに記録されます。 次に、受信した情報と矛盾するものが列レイアウトから削除され、列が検索されます(グリッド内に少なくとも1つのアスタリスクが現れるまで検索が続行されます)。
While
ループの動作を説明する必要はないと思います。 上記のコードの
MemberQ
は、グリッドにアスタリスクがある場合は
True
返し、そうでない場合は
False
返します。
Transpose
、行と列の両方で同等に作業できるようにも使用されます。 画像を表示するために、セルが1の場合は黒、0の場合は白(デフォルトではアスタリスクは茶色)を
ArrayPlot
する組み込み
ArrayPlot
関数があります。 ソリューションプロセス中にパターンがどのように動的に変化するかを確認するには、
Dynamic
使用します。
Dynamic[ArrayPlot[pic, Mesh->True]]
While[MemberQ[pic, "*", 2],
pic = findInformation /@ rowpos;
colpos = MapThread[deleteFromList, {colpos, Transpose[pic]}];
pic = Transpose[findInformation /@ colpos];
rowpos = MapThread[deleteFromList, {rowpos, pic}];]
結果はこの写真です:

おそらく誰かがソリューションが非常に最適ではないことに気づきました。 はい、そうですが、最適性はポイントではありません。 この記事の目的は、Wolfram Mathematicaがこのような問題を便利かつ迅速に解決できることを示すことです。 しかし、すでに最適化について話している場合、このタスクのアルゴリズムを最適化する方法は多数あります。たとえば、このバージョンのプログラムでは、セル情報が前の手順で追加された列および行のみの情報をフィルタリングおよび検索し、すべての列で検索が実行されます行。