この一連の記事では、できるだけ単純に複合体について話そうとします。 その結果、特定の時点での地球の表面上の特定のポイントについて、太陽系の惑星を探す場所を指示する簡単なプログラムを作成します。 私の目標は、軌道のケプラーモデルの背後にあるものの本質を読者に伝えることです。そのため、ニュートンの法則と万有引力の法則以外の既知の事実は使用しません。
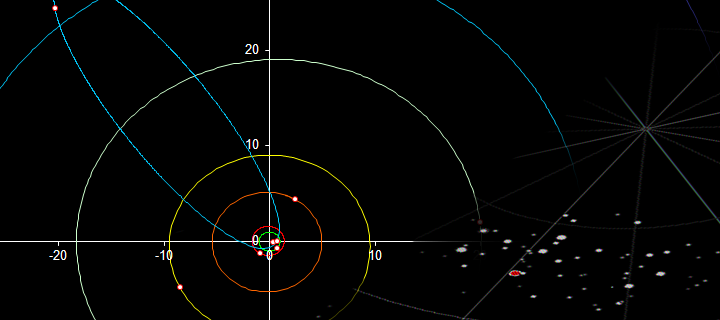
猫の下にいるすべての好奇心を尋ねます。
読者がニュートンの法則、幾何学からの基本情報、ベクトル代数、微分計算にある程度精通していることを意味することは注目に値します。
それでは、惑星はどのように動くのでしょうか？
実際には、惑星の相互の影響、太陽の重心に対する太陽系の重心の変位などを考慮すると、 惑星運動は非常に複雑で、厳密な分析の定義を受け入れられません。 3体の動きの問題でさえ分析的に解決できないことに注意する価値があります。 したがって、どのモデルを使用するかというフレームワーク内ですぐに規定しましょう。 ケプラー軌道モデルを検討します。 他にも多くのモデルがありますが、それらはすべて半解析的であり、その結果、それらのほとんどは、ケプラー軌道のパラメーターを興味深い瞬間に決定することになります。 つまり、ケプラーの軌道は、特定の時点での惑星の複雑な動きの近似値です。 ケプラーの惑星の軌道パラメーターはnssdc.gsfc.nasa.gov/planetary/factsheetにあります。また、これらのケプラーの軌道パラメーターが天体の正確な位置を与える時代（言い換えると、時点）も示されています。 通常、この開始時点はJ2000.0（2000年1月1日正午）の時代です。 ケプラーモデルを使用した短時間の物体の動きの計算は非常に正確です。 精度は、視覚的にまたは小さな望遠鏡でエラーに気付かないほど十分です。 もちろん、別の惑星への飛行経路を計算するには、より正確なモデルが必要です。
ケプラーの軌道
だから、順番に。 このモデルの基本的な仮定から始めましょう。 太陽の質量は結合されたすべての惑星の質量よりもはるかに大きいと想定されており、このことから、惑星と惑星間の相互作用は太陽と惑星間の相互作用に比べて無視できると結論付けることができます。 したがって、前述のタスクを使用して、2つの物体の相互作用の問題を解決できます（つまり、各惑星と太陽との相互作用を個別に考慮することができます）。 さらに、惑星の質量は太陽の質量よりはるかに小さいと仮定し、相互作用は片側、つまり 惑星は太陽の動きに影響しません。 したがって、惑星は、重力場内を移動する物質的な点と見なすことができ、その中心は動かない。 このようなもの：
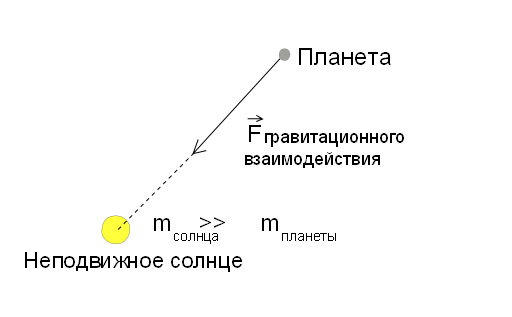
重力相互作用
重力相互作用とは何ですか？ これは、すべてのマテリアルボディ間の普遍的な基本的な相互作用です。 重力について長い間話すことができますが、重要なことだけが必要です。 ニュートンの古典的な重力理論によれば、距離Rで分離された質量m 1とm 2の2つの物質点の間の重力引力は、両方の質量に比例し、それらの間の距離の2乗に反比例します。
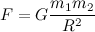
ここで-Gは重力定数（特定の比例係数）です。 重力は、ある物体の重心から別の物体の重心に向けられ、それらの間の距離の二乗に反比例することに注意してください（逆二乗の法則）。
太陽の側面からの引力を除いて、物質点の
ニュートンの第二法則
力の影響下で体はどのように動くのですか？ ニュートンの第二法則はこの質問に答えます。 一般に、この法律にはいくつかの定式化があり、最も一般的な定式化があります。
慣性基準システムでは、質点によって取得される加速度は、それを引き起こす力に直接比例し、方向でそれと一致し、質点の質量に反比例します。
この表現は正確ですが、あまり明確ではありません。 ニュートン自身が異なる定式化を行った：
運動量の変化は、加えられた駆動力に比例し、この力が作用する直線の方向に発生します。
この言い回しは、それほど正確ではありませんが（レポートシステムについて予約する必要がありますが、これはまだ興味の対象ではありません）、はるかに理解しやすいものです。 ここで、運動量は、身体の質量とその速度の積に等しい、いわゆる身体の運動量を意味すると理解されます。
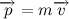
したがって、シンボリック形式で言葉遣いを書きます。
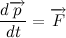
あるいは、体の運動量が何であるかを書き留めて、微分符号の質量を定数として取り出す（質量は常に定数ではありませんが、この場合は定数です）と、次のよく知られた式が得られます。
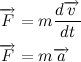
ベクトルはどこですか
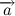-体の加速。 加速度、運動量、速度、力はベクトル量であることを忘れないでください。 ベクトルの符号がベクトル量を上回る場合、理解されるのはベクトルであり、それ以外の場合はそのモジュールであることに同意しましょう。
ケプラーの第二法則
簡単にするために、重心に原点を置きましょう。 太陽の重心に。 したがって、惑星の重心から原点に引かれたベクトルは、重力のベクトルと方向が一致します。
空間における身体の位置は、いわゆる半径ベクトル、つまり身体の原点から重心までのベクトルによって記述されます。 式の左側と右側に半径ベクトルをベクトルで乗算します。
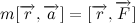
さらに操作するために、ベクトル積の導関数を書きましょう。
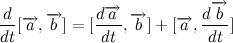
次に、ベクトル積の導関数は、速度によるベクトルの半径です。
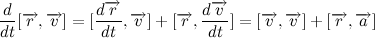
それ自体のベクトルのベクトル積がゼロであることを思い出させてください。
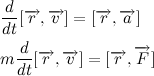
微分符号の下に質量を導入し、取得する身体の運動量の式を考慮に入れます。
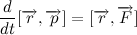
重力のベクトルは常に重心に向けられているため、ベクトルの半径と重力のベクトル積は常にゼロであるため、非常に重要な結論を下します。
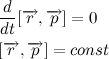
角運動量の保存のいわゆる法則を得ました。 物体の角運動量の変化は、それに適用される角運動量に比例します。 重力ベクトルは常に重心の方向を向いているため、重心に対する重力のモーメントは常にゼロです。 したがって、身体の角運動量は一定です。
惑星の質量は一定であることに同意したため、次の式も当てはまります。
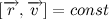
何であるかを理解する
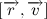写真を見てみましょう：
この図は、軌跡の一部を示しています。 時間dtの間、身体は距離vdtを移動します。 ベクトルのベクトル積のモジュールは、これらのベクトル上に構築された平行四辺形の面積に数値的に等しくなります。 それは次のことがわかります：
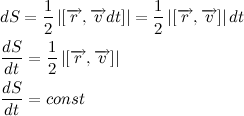
価値
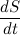単位時間あたりのベクトルの半径によって記述される領域があり、それはセクター速度と呼ばれます。 その結果、体の扇状速度は一定です。 ケプラーの第2法則があります：
各惑星は、太陽の中心を通る平面内を移動し、同じ期間、太陽と惑星を結ぶ半径ベクトルは等しい面積を表します。
はい、「法律を知った」というのは良く聞こえませんが、何ができるのか、それはそう呼ばれています。 理由は、ケプラーがそれを導き出さなかったが、彼の観察に基づいて直感的にそれを選択したことです。 経験的にそれを受け取った、この場合それは本当に法律でした。
以下はこの法律の実例です（図はウィキペディアの記事から引用しています）。
微分軌道方程式
それにもかかわらず、ベクトルの半径と速度のベクトル積を詳しく見てみましょう。 半径ベクトルは、モジュールのベクトルの半径（原点から点までの距離）と、ベクトルの半径と方向が一致する単位長さのベクトルの積として表すことができます。
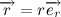
速度ベクトルは次のようになります：
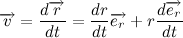
そして、ベクトル積はベクトルの半径と速度です：
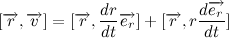
ベクトルという事実を考えると
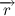そして 
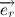方向が一致するため、方向とベクトルが一致する 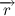そして 
私たちはそれを得る 
。 次に：
時間に関する単位ベクトルの導関数を見てみましょう。
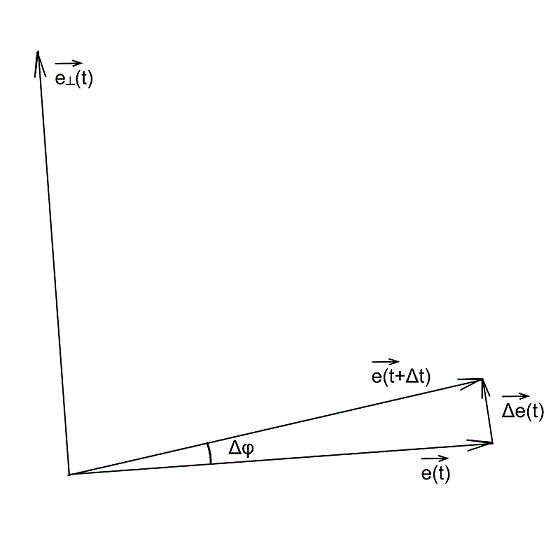
図は時間内にそれを示しています
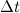ベクトル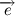 
ピボット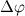 
。 差分ベクトル 
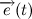そして 
ベクトルに等しい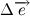 
。 小さな角度の場合、次の関係が成り立ちます。
限界では、いつ
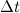ゼロになる傾向、ベクトル方向 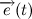そして 一致し、ベクトルの方向 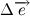それらに垂直。 単位ベクトルを紹介します 
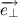に垂直 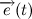そして、その端の動きの方向と一致し、それから：
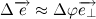
したがって、限界に達すると、次のようになります。
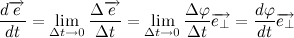
どこで
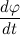これはベクトルの角速度で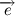す 。 示す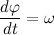 
速度の半径ベクトルを製品に戻しましょう。
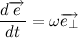私達は得る：
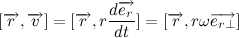
ベクトルが
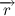そして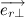 
相互に垂直。 もう一つの単位ベクトルを紹介します 
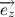これはベクトルに垂直です 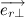そして 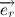。 したがって、ベクトル 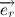、 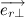そして 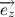正規直交基底を形成します。 ベクトル積の定義に基づいて、以下を取得します。
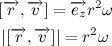
だから
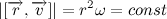。 表記を紹介します 
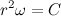。 次のことに注意する価値もあります。
ニュートンの第二法則に戻りましょう。 身体に作用する力ベクトルは、重力の値に単位ベクトルを掛けた値としてすぐに記述できます。
：
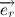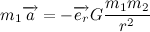
ここで、m 1とm 2はそれぞれ惑星と太陽の質量です。
すぐに惑星の質量を減らしましょう。惑星の質量は、運動の軌跡にまったく影響しないため、他のどこにも思い出せません。 単位質量体で作業していると仮定します。 表記を紹介します
その後：
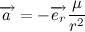
加速ベクトルを書きましょう：
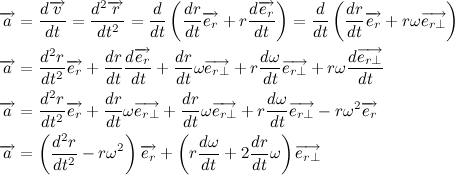
2番目のブラケットの内容を考慮してください。
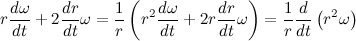
しかし、私たちはすでにそれを知っています
、その結果 
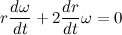その後：
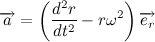
表記を紹介します
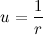。 先に記法を導入したことを思い出させてください 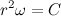明らかに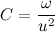 
。
次に、モジュールの導関数、Cを通るベクトルの半径を記述します。
次に、モジュールの2次導関数、Cを通るベクトルの半径を記述します。
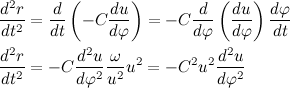
結果が与えられたら、加速ベクトルの式を書き直します。
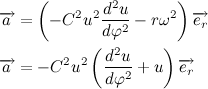
次に、ニュートンの第2法則は次の形式をとります。
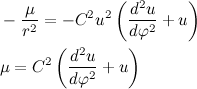
結果の微分方程式をより馴染みのある形に書き換えます。
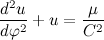
多くの人が微分方程式の結果を推測していると思いますが、読者と私に負担をかけすぎないように、この最初の部分を終了するでしょう。
まとめ
重力場における物質点の軌道を記述する微分方程式を受け取りました。これは、惑星や他の天体の軌道を記述するのに非常に適用できます。
私たちがまだ持っていること
結果の微分方程式には時間パラメータがないため、動きの性質については何もわかりませんので、何らかの方法で時間にバインドする必要があります。 また、観測者に接続されたシステム内の惑星の座標を取得するために、さまざまな座標系とその変換が考慮されます。
PS
どんな批判、コメント、追加も大歓迎です。