
KDPV:生きている例に関するランドセル問題
背景
私が中学3年生のとき、それはすべて10年前に始まりました。 私は偶然、コンピューターサイエンスの教師が長老の1人にパズルを話す会話を耳にしました。数字のセットが与えられ、別の数字がコントロールでした。 セットから番号の最大合計を見つける必要がありますが、これは管理番号を超えません。
何らかの理由でタスクが私の魂に沈みました。 家に帰ってから、私はすぐに解決策を考え出しました。最良の選択肢を選べる可能なすべての金額の素朴な検索です。 すべてのNビットの2進数を並べ替え、ユニットが対応する初期番号の合計を取ることで、組み合わせを取得しました。 しかし、残念ながら、要素の数が30前後から始まるため、プログラムが非常に長い間実行されることがわかりました。 そのようなアルゴリズムの動作時間はn * 2 n (組み合わせの数に合計の長さを掛けた値)であるため、驚くことではありません。
5年が経過しました。 私は何とか学校を卒業して大学に行きましたが、この仕事はまだ私にありました。 「プログラマーのためのアルゴリズムトリック」(Hacker's Delight / Henry S. Warren Jr.)の本に目を通すと、グレイコードの説明に遭遇しました。 「やめて!」と思った。「それは...はい!」 これは、検索の各ステップでの問題において、全体の金額を計算することはできず、1つの数値を加算または減算することを意味します。 そして、私はすぐにトピックの研究に深く入りました。
グレーコードの作成
グレーコードは、多くのビット深度に対して構築できます。 1つのカテゴリについては明らかです。
0
1
2番目の数字を追加するには、このシーケンスに同じものを逆方向に追加できます
0
1
1
0
後半にユニットを追加します。
00
01
11
10
同様に3桁の場合:
000
001
011
010
110
111
101
100
低ビット容量のコードを反映して得られるこのようなコードは、反射(反射)グレーコードと呼ばれます。 他のシーケンスもありますが、実際にはこれが通常使用されます。
このコードは、このコードでデジタル信号を生成した真空管ADCを発明したFrank Grayにちなんで命名されました。 入力信号レベルのわずかな変化により、デジタル出力は1ビットでのみ変化する可能性があり、これによりビットの非同時スイッチングによる突然のジャンプが回避されました。
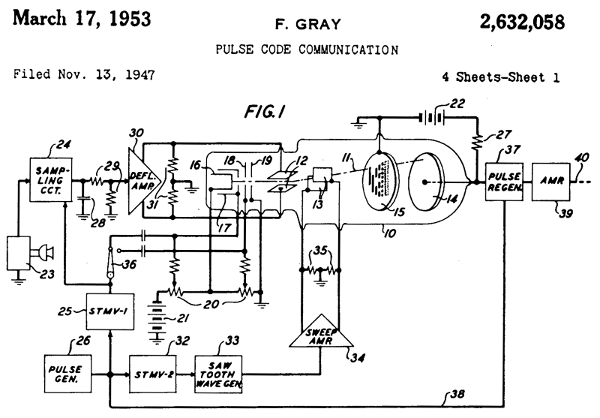
フランク・グレイの特許イラスト
グレイコードの最も明らかな使用法は、角度センサーです。 古い機械式マウスにあったものと同様のセンサーですが、相対変位ではなく、角度の絶対値を決定します。 これを行うには、各センサーに複数のオプトカプラーと複数のスロット付きグレーティングが必要です。 さらに、センサーの後続の各位置は、1ビットの状態でのみ前の位置と異なる必要があります。そうでない場合、境界でビットの非同期切り替えが可能になり、その結果、デバイスの読み取り値が急激にジャンプします。 ここで、グレイコードの奇妙な特徴を見ることができます。最後の数値も最初の数値と1ビットずつ異なるため、「ループ」できます。

絶対回転角のセンサー。 光スロットはグレーコードに従って配置されます。
ナップザック問題への応用
しかし、ナップザック問題に戻ります。 標準の式は、番号によるグレイコードを提供します。
G = i ^ (i >> 1)
それによると、必要なすべての要素の合計しか計算できません。 そして、各反復で1つの値を加算または減算しますか? したがって、変更されたビットの数を取得する必要があります。 複数桁の番号の場合、これらの番号は次のようになります。
0
1
0
2
0
1
0
3
0
1
0
2
0
1
0
4
...
何にも似ていませんか? これは、通常の2進数をリストするときに1に設定するビット数です。 または、2進数のマイナーユニットの番号。 この操作は、最初のセットの検索と呼ばれ 、ほとんどのプロセッサには個別の命令として存在します。 Visual C ++は、この命令を_BitScanForward関数として提供します。
これで、グレイコードを介してナップザックの問題を解決するプログラムを作成する準備が整いました。 次のように問題を定式化します。
input.txtファイルでは、最初の行はバックパックの容量を示し、残りの行は物のサイズを示します。 コンソールでは、バックパックの最大負荷と選択したもののサイズを表示する必要があります。 入力などの正確性を確認する-を参照してください。
使用済みのビットマスクを保存し、必要に応じてそれらの1つを追加または削除します。 intで対応するために、もの(および使用されるビット)の数を31に制限します。
#include <iostream> #include <fstream> #include <bitset> #include <intrin.h> using namespace std; void main() { int target; // int nItems = 0; // int weight[31]; // ifstream inFile("input.txt"); inFile >> target; while(inFile >> weight[nItems]) nItems++; inFile.close(); const unsigned int nIterations = 1 << nItems; // , 2^n int sum = 0; // int bestSum = 0; // ( ) bitset<31> mask; // bitset<31> bestMask; // for (unsigned int i = 1; i < nIterations; i++) { unsigned long position; // _BitScanForward(&position, i); mask[position] = !mask[position]; if (mask[position]) // sum += weight[position]; else sum -= weight[position]; if (sum > target) // continue; if (sum > bestSum) // ! ... { bestSum = sum; bestMask = mask; } } cout << "Best approximation: " << bestSum << endl; cout << "Used weights:" << endl; for (int i = 0; i < 31; i++) if (bestMask[i]) cout << weight[i] << endl; cin.get(); }
粗さの可能性をおIびします。 残念ながら、C ++は長い間私のコア言語ではありませんでした。
すべての合計をゼロから組み立てるよりも本当に速く動作し、20の数字で違いがすでに顕著であり、30では、新しいバージョンが7秒で完了するまで、ナイーブアルゴリズムが完了するのを待ちませんでした。 ただし、指数関数的な複雑さを考えると、これはかなりの量です。50個の数値では、このアルゴリズムを使用しても意味がありません。 残念ながら、正確なアルゴリズムは2 nよりも速く動作しません。 より高速な近似解のみが可能です。 (更新:場合によっては、動的プログラミングと中間者が問題をより迅速に解決します。詳細についてはコメントを参照してください。)
おそらくそれが、このプログラムをスピードアップしようとして、人生の終わりまでランドセルを運ぶ運命にある理由です。 アセンブラでサイクルを一度書き直しましたが、速度が少し上がりましたが、今ではプログラムのマルチスレッドバージョンを作成することさえ考えています。 あなたは私に同情することができます。 :)