円錐形のセクション

先日、幾何学的計算に関連するプログラムの断片をデバッグしているときに、入力パラメーターの値に関係なく、変数の1つが同じ値を持つことに気付きました。 当然、まず第一に、間違いを疑い、それを探すのにしばらく時間を費やしましたが、少し考えた後、これは間違いではなく、忘れられがちな円錐曲線の既知の特性の1つであることに気付きました。 その後、私はより多くの時間を美しい幾何学的な構造を描くことに費やし、最終的に誰かと写真を共有する価値があると判断しました。 そこで、この金曜日の記事が登場しました。



楕円、放物線、双曲線などの曲線は円錐セクションと呼ばれることを思い出させてください（そして、高等数学を勉強しなかった人たちに知らせます）（まだ縮退している場合があります-今からは説明しません）。 一般に、円錐形のセクションは非常に素晴らしいオブジェクトであり、多くの分野で見られます。 たとえば、放物線アンテナや天体の軌道を思い出すかもしれません。

各円錐セクションは、円錐のセクションです（CEPですか？）。つまり、円錐と平面が交差するときに形成される線です。 まあ、外観は平面の相対的な位置と円錐の母線に依存します。 このような線がすべて2次方程式のグラフであることを証明するのも簡単です。



高等数学を教えた人は誰でも、二次の線と面の分類を覚えるのにある程度の時間を費やしたでしょう（特に想像上の数字を考慮に入れない場合は、神にとってあまり多くの言葉はありません）。



しかし、楕円、放物線、双曲線の古典的な定義には、別のプロパティが使用されます（Wikipediaを引用）。

楕円は、ユークリッド平面の点の幾何学的位置であり、2つの与えられた点（焦点と呼ばれる）への距離の合計は一定であり、これらの点間の距離よりも大きくなります。



双曲線は、選択された2つの点（焦点と呼ばれる）への距離の差の絶対値が一定であるユークリッド平面の点の幾何学的位置です。



放物線は、指定された直線と指定された点から等距離にあるユークリッド平面の点の幾何学的な場所です。



これらのプロパティの証明は簡単です。 対応する二次方程式を取り、距離の式を慎重に記述し、代数変換を行う必要があります。 計算はかなり面倒なので、ここでは最も単純な場合、放物線のみを示します。



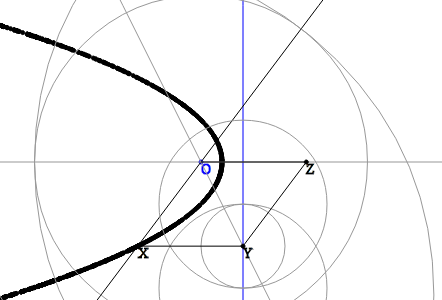
「点の幾何学的な場所」という用語は、すぐに学校の机とコンパスと定規を備えた構造物に似ています。 一般に、代数的に作用する方が簡単な場合が多いのですが、ジオメトリの私のお気に入りの部分でした。 もちろん、コンパスと定規を使用して円錐セクションを完全に構築することは不可能ですが、これらの曲線上にある任意の数のポイントを構築できます。 これを行う最も簡単な方法は、上記のプロパティを使用することです。 楕円のこのような構造を検討してください。





OとQを楕円の焦点とし、2aを距離の合計とします。 焦点Oを通る線を取り、点X（線と楕円の交点）を考慮します。 同じ直線上に2aに等しいセグメントOYを置くと、三角形QXYが得られます。 楕円の特性により、QX + OXは2aに等しくなります。これは、QX = XYであり、示された三角形が二等辺であることを意味します。 これにより、QYに垂直な中央をプロットすることにより、ポイントXを簡単に再構築できます。





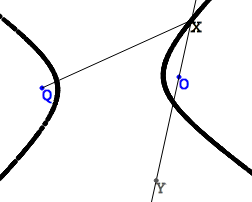
双曲線の場合、構造は類似しており、ポイントYのみを他の方向に脇に置く必要があります。 OYはセグメントXYとOXの差であり、三角形QXYはまだ二等辺であることがわかります。 構築アルゴリズムは同じであるため、正確にはどうなるか-楕円または双曲線は、焦点間の距離が大きいか、合計（差）を指定するセグメントの長さが大きいかによって異なります。









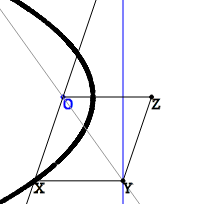
放物線の場合はもう少し複雑です。 Oを放物線の焦点とし、監督を与えます。 二等辺長方形の代わりに、ここでは、XYとOZの線が直行軸に垂直であるOXYZ平行四辺形を考慮する必要があります。 したがって、放物線の特性XY = XOにより、この平行四辺形は菱形になります。 直線OXがあるため、菱形を復元して点Xを見つけるのは難しくありません-角度XOZの二等分線を描くだけで十分です-二等分線と直行線の交点として点Yを取得し、この点から定義線との交点までの垂線を復元します。



放物線を描くプロセスは、次のビデオに記録されています。





さて、誰もが自分で構造のシーケンスを確認し、設定ポイントを移動し、補助円の魅惑的な動きをここで観察できます 。 「ドラッグしてください」というラベルの付いたドットを忘れずに移動してください。