Clever Geek Handbook

サルと無限の仕事

タイプライターに猿を置いて、常に誤ってキーをたたくと、遅かれ早かれ、戦争と平和、ピタゴラスの作品のコレクション、そして今読んでいる記事を印刷することは誰もが知っています。









驚くべき事実ですが、さらに興味深いのは、特定のテキストを入力するのにどれくらい時間がかかるかを理解しようとすることです。 余分なパラメーター（猿によるタイピングの速度）を駆動させないために、質問に対する答えを探します。キーストロークは平均で何回かかりますか。 文字列「abc」の方が「aaa」よりはるかに簡単に入力できることは明らかですか？ この投稿はこの問題を解決することに専念しています。 途中で、関数のプレフィックスとそのプロパティについて説明します。







サルが特定のテキストの入力に費やす時間は、ランダム変数であることが明らかです。 したがって、彼女の数学的な期待について尋ねることは論理的です。











問題の正式な声明



大文字のラテン文字（ "a"-"z"）で構成される文字列sが与えられます。 マットを見つける必要があります。 すべての文字が平等に入力される場合（確率1/26 ）、文字列s全体が入力される前に、ランダムなキーストロークの回数を待機します。







決定コード

これがなぜ機能し、このPi（）関数が何であるかを理解するには、記事全体を読む必要があります:(。 







string s; //,    int n = s.length(); vector<int> p = Pi(s); vector<long double> pow(n+1); pow[0] = 1; int i; for (i = 1; i <= n; i++) { pow[i] = pow[i-1]*26; } long double ans = 0; for (i = n; i>0; i = p[i-1]) { ans += pow[i]; } cout << ans;






プレフィックス機能



この機能は、問題の解決に役立ちます。 関数プレフィックスは、文字列内の部分文字列を見つける有名なアルゴリズム（ KMPアルゴリズム）のために、D。KnutとM. Pratt（およびD. Morrisに類似）によって導入されました。 文字列sのプレフィックス関数は、最長のネイティブ文字列プレフィックスの長さを返します。これは、そのサフィックスでもあります。







プレフィックスとサフィックス

末尾からいくつかの文字を破棄する場合、プレフィックスは行の先頭にすぎません。 したがって、行「aba」には4つのプレフィックスがあります。「」（空行）、「a」、「ab」、「aba」です。 接尾辞は同じですが、文字は先頭から削除されます。 ただし、一部の接尾辞と接頭辞は一致する場合があります。 文字列「aba」には、「」、「a」、「aba」の3つの接頭辞接尾辞があります（4番目の接尾辞「ba」は接頭辞「ab」と一致しません）。 サフィックスまたはプレフィックスは、行全体より短い場合に適切と呼ばれます 。







正式に言えば： \ pi（s）= max \ {k \、| \、0 \ le k＆lt; | s |、\、pref_k（s）= suf_k（s）\}







ここで、 pref k （s）は文字列sの長さkのプレフィックスであり、 suf k （s）は文字列sの長さkのサフィックスです。







ILCアルゴリズムと他のアプリケーションの両方で、特定の文字列のすべてのプレフィックスに対してプレフィックス機能をすぐに検討する方がはるかに便利です。 はい、恐ろしいですね-プレフィックスごとに、サフィックスのサフィックスと一致する最大のカスタムプレフィックスを見つける必要があります。 しかし実際には、すべてが簡単です。











\ pi_s（k）= \ pi（pref_k（s））、\、1 \ le k \ le | s |










このような拡張プレフィックス関数は、単純な計算よりも計算が簡単なため、主に役立ちます。 \ pi（s） 。 以下の値 \ pi_s（k） s = "ababac"の場合。 







  k：1 2 3 4 5 6
    s：アババク
 P（i）：0 0 1 2 3 0






計算関数のプレフィックス







計算コード 
 vector<int> Pi(string s) { int n = s.length(); vector<int> p(n); p[0] = 0; for (int i = 1; i < n; i++) { int j = p[i-1]; while (j > 0 && s[i] != s[j]) { j = p[j]; } if (s[i] == s[j]) j++; p[i] = j; } return p; }


関数プレフィックスの簡単なO（N）計算は、2つの単純な観測に基づいています。







（1）位置kの接頭辞接尾辞を取得するには、位置k-1のある種の接頭辞接尾辞を取り、位置kの記号の最後に追加する必要があります。







（2）長さnの文字列sのすべての接尾辞接頭辞は、次のように取得できます。 \ pi_s（n）、\、\ pi_s（\ pi_s（n））、\、\ pi_s（\ pi_s（\ pi_s（n））） 次の値が0になるまで続きます。このプロパティは、「abacaba」行で確認できます。 ここに \ pi_s（7）= 3、\、\ pi_s（3）= 1、\、\ pi_s（1）= 0 、これはすべてのプレフィックスとサフィックス（「aba」、「a」、「」）に対応します。 これは、プレフィックスの最大サフィックスの長さが \ pi_s（n） 。 次のプレフィックスサフィックスは短くなります。 ただし、最初のプレフィックスサフィックスは行sの先頭と末尾の両方にあるため、次のプレフィックスサフィックスは最初のプレフィックスサフィックスの中で最も長いプレフィックスサフィックスになります。







したがって、位置iの関数接頭辞を構築するには、前の位置の関数接頭辞の値から、接尾辞が新しい文字で続き、接頭辞になるまで繰り返すだけで十分です（このため、新しい文字を1つだけチェックする必要があります）。 このようなアルゴリズムは線形時間で実行されます。これは、関数のプレフィックスの値が毎回最大1増加するため、 n回以上減少することはできないため、ネストされたループが合計n回以下で実行されることを意味します。











KMPステートマシン



問題を解決するために必要な次の数学的オブジェクトは、特定の文字列sで終わる行を受け入れる有限状態マシンです。 このオートマトンは、あまり知られていない別のKnuth-Moriss-Prattアルゴリズムの修正で使用されます。 このバージョンのアルゴリズムでは、特定の行（テンプレート）で終わるすべての行を受け入れる状態マシンが構築されます。 次に、テキスト文字列がマシンに送信されます。 マシンが渡されたテキストを受け入れるたびに、テンプレートの次の出現が検出されます。 タイプライターの背後にある猿の問題を解決するのに役立つのはこのマシンです。







有限状態マシンとは

ステートマシンは、ある種の内部状態を持つボックスとして想像するのが最も簡単な数学的オブジェクトです。 最初は、ボックスは初期状態です。 ボックスには、一度に1文字ずつ行を入力できます。 各シンボルの後、現在の状態と入力されたシンボルに応じて、ボックスの状態が変わります。 また、一部の状態は良好です（数学用語は最終状態です ）。 彼らは、この文字列を文字ごとに与えた後、マシンが良好な状態にある場合、オートマトンは文字列を受け入れると言います。







宇宙船を決定するには、初期状態、良好な状態、および遷移関数を決定する必要があります-状態とシンボルごとに、オートマトンが入る新しい状態を指定する必要があります。 オートマトンを完全な方向のグラフとして描画すると便利です。この場合、頂点は状態であり、各エッジに1つのシンボルのみが書き込まれます。 各頂点には、各シンボルに正確に1つのエッジが必要です。 次に、行を処理するには、この行の文字をエッジに沿って移動するだけです。 パスが最終状態で終了した場合、マシンはそのような文字列を取得します。







このオートマトンを作成するには、すでに知っているプレフィックス関数を使用します。

マシンには0からnまでの番号が付けられたn + 1の状態があります。 状態kは、長さkのパターンのプレフィックスを持つ最後に入力されたk文字の一致に対応します（文字列「abac」を検索する場合、最後の現在のテキストに関心があります：「abac」、「aba」、「ab」、「a」またはwhatこれは、1文字を追加した後に同じ結果を得るのに十分です）。 状態0は初期状態で、状態nは最終状態です。 混乱が生じる場合があります。たとえば、「zzzabab」という行に自動的にフィードされる「ababccc」という用語では、状態2と4の両方を選択できます。ただし、入力したテキストに関する必要な情報を失わないように、常に最高の状態を選択します。







KMPステートマシンの例

文字列「ababac」のマシンは次のとおりです。 たとえば、アルファベットは「a」〜「c」の文字のみで構成されます。 明確にするために組み合わされた平行リブ。 実際、各エッジに対応する文字は1つだけです。 初期状態は0 、最終状態は6です。





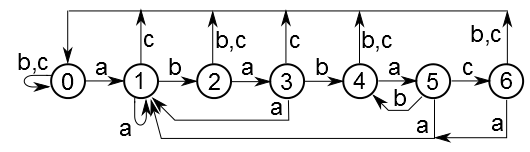
状態0から状態6へのパスは、それがどれほど困難であっても、文字列「ababac」で終わることを確認するのは簡単です。 逆に、このようなパスは必ず状態6で終了します。







ステートマシン構築コード 
 string s; // . int n = s.length(); vector< vector<int> > nxt(n+1, vector<int>(256)); //   nxt[][] ==   vector<int> p = Pi(s); //  . .   nxt[0][s[0]] = 1; //    0   0. for (int i = 1; i <= n; i++) { for (int c = 0; c < 256; c++) nxt[i][c] = nxt[p[i-1]][c]; //p[]   ,   -1 if (i < n) nxt[i][s[i]] = i+1; }


遷移の構築方法に注意してください。 状態iからの遷移を計算するには、2つのオプションを検討します。 新しい文字がs [i]の場合、遷移は状態i + 1になります。 ここではすべてが明らかです。i文字に一致があった場合、文字列sから次の文字を追加すると、一致の長さが1増加します。 シンボルが一致しない場合、状態から遷移を単にコピーします \ pi_s（i） 。 なんで？ この場合の遷移は、番号≤iの状態に正確になります。 そのため、移行後、入力したテキストに関する情報の一部を忘れます。 先に進む前にこれを行うことができます。 消去できる最低限は、実際には状態がiではないふりをすることですが、 \ pi_s（i） 。 上記の例のように、テキストが「abab」または「ab」で終わると考えることができます。 「abab」からの移行がない場合は、「ab」からの移行を使用できます。











解決策



これでタスクを解決する準備ができました。

stringのKMPオートマトンを構築します。 すべての文字はランダムに猿によって入力されるため、シンボル自体は重要ではなく、遷移グラフのエッジのみが重要です。 問題は次のように再定式化できます。マットを見つけます。 状態0から状態nに到達するまでのランダムウォークで遷移の数を待機します。







この定式化で変数を導入することは論理的です： E k 、0≤k≤n-状態nに達するまでの遷移の数の期待。 E 0が元の問題の答えになります。 Zを有効な文字（アルファベット）のセットにします。 連立方程式を作成できます。











E_n = 0














E_k = 1 + \ frac {1} {| Z |} \ sum_ {c \ in Z} {E_ {nxt [k] [c]}}、k = 0..n-1










方程式（1）は、状態nに到達するとランダムウォークが停止することを意味します。

他の状態では、何らかの遷移が行われるため、式（2）に用語1が存在します。 2番目の項は、すべての可能なオプションの合計にこれらのオプションの確率を掛けたものです。 すべての確率は同じです。したがって、合計のサインとして取り出されます。







O（n ^ 3）には既に問題の解決策があります。構築された線形方程式系は、ガウス法によって解くことができます。 しかし、このシステムを少し見て、関数の接頭辞があることを覚えていれば、つまり、解決策ははるかに簡単で高速です。







有限状態マシンの構築を思い出してください。 （簡単にするために、 \ pi_s 私はちょうど使用します \ pi ） 状態kからの遷移は、状態からの遷移とほぼ一致します \ pi（k） 。 遷移の違いは、シンボルs [k-1]のみです。 したがって、状態kおよび状態の方程式（2）の右辺 \ pi（k） 1つの用語のみが異なります。 の方程式で \ pi（k） 価値がある E_ {nxt [\ pi（k）] [s [k-1]]} の代わりに E_ {nxt [k] [s [k-1]]} kの方程式で。 さらに、 nxt [k] [s [k-1]] = k + 1です。 この事実を使用して、方程式（2）を書き換えることができます。











E_k = E _ {\ pi（k）} + \ frac {1} {| Z |}（E_ {k + 1} -E_ {nxt [\ pi（k）] [s [k-1]]}）










次に、もう1つ観察する必要があります。 わかった











nxt [\ pi（k）[s [k-1]] = \ pi（k + 1）










つまり 状態の関数接頭辞を見つけるには、前の状態から関数接頭辞を取得し、そこから次の状態につながる記号をたどる必要があります。

確かに、状態を考慮すると \ pi（k） 、それは文字s [k-1]で終わる行に対応します。 そのため、このシンボルには遷移があります。 そのような遷移が存在するが、番号<kを持つ最大の状態を考えます。 シンボルs [k-1]の後に何らかのサフィックスが付いた場合 pref_k（s） その後、遷移前に接尾辞でした pref_ {k-1}（s） 。 これは右端のそのような状態だったため、最大プレフィックスサフィックスに対応します。 pref_ {k-1}（s） 、つまり数字があることを意味します \ pi（k-1） 。 だから、この驚くべき有用な事実を得た。







次に、（3）は次のように変換されます。











E_k = E _ {\ pi（k）} + \ frac {1} {| Z |}（E_ {k + 1} -E _ {\ pi（k + 1）}）










または別の方法で：











| Z | （E_k-E _ {\ pi（k）}）=（E_ {k + 1} -E _ {\ pi（k + 1）}）










等号の両側には負の数があります（ kが多いほどE kが小さくなることが論理的です）。 両側に-1を掛けます。











| Z | （E _ {\ pi（k）}-E_k）= E _ {\ pi（k + 1）}-E_ {k + 1}










ただし、（4）はk> 0に対してのみ有効です。 k = 0の場合、式（2）を明示的に記述できます。 遷移は状態1につながり、残りはすべて状態0に戻ります 。











E_0 = 1 + \ frac {1} {| Z |} E_1 + \ frac {| Z | -1} {| Z |} E_0










ここで、左側のすべての変数を収集し、方程式に| Z |を掛けます。 そして交換 0 = \ pi（1） （1文字には空でないプレフィックスがないため、1文字のプレフィックス関数は常に0です）：











E _ {\ pi（1）}-E_1 = | Z |










方程式（1）、（4）、および（5）を繰り返すことができます。これは、これらが方程式を解析するシステムを構成するためです。











E _ {\ pi（1）}-E_1 = | Z | \\ | Z | （E _ {\ pi（k）}-E_k）= E _ {\ pi（k + 1）}-E_ {k + 1}、\、k = 1..n-1 \\ E_n = 0










2番目の左側の最初の方程式をk = 1で置き換え 、次にk = 2などで置き換えます 。 私達は得る：











E _ {\ pi（k）}-E_k = | Z | ^ k、\、k = 1..n










これで、解決策はほぼ準備できました。今、 k = nについて（6）を検討し、 E_n = 0 私達は得る：











E _ {\ pi（n）} = | Z | ^ n










（6）のこの値を k = \ pi（n） -私達は得る：











E _ {\ pi（\ pi（n））} = | Z | ^ n + | Z | ^ {\ pi（n）}










同様に、以下を取得します。











E _ {\ pi（\ pi（\ pi（n）））} = | Z | ^ n + | Z | ^ {\ pi（n）} + | Z | ^ {\ pi（\ pi（n））}










したがって、次の式を取得するまで続行できます。 E_0 、ついでに、問題に対する答えです。 示す \ pi ^ k 行にk回適用される関数 \ pi その後：











E_0 = \ sum_ {k：\ pi ^ k（n）＆gt; 0} | Z | ^ k










したがって、O（n）の問題の解決策を得ました。文字列sの関数のプレフィックスを作成し、 0に達するまでnから繰り返し、同時に度| Z |を加算します。 プレフィックスの現在の長さと等しい。 これは、記事の冒頭で示したまさにその解決策です。







（*）を見ると、文字列「aaa」が「abc」よりも入力が難しい理由が明らかになります。「aaa」では3番目の反復のみ \ pi ゼロであり、2行目には通常、接尾辞に等しい空でない接頭辞はありません。 \ pi すぐにゼロになります。











備考



プレフィックス関数とILCマシンは、文字列を操作するための非常に便利なツールです。 親愛なる読者が興味を持っているなら、私は他の問題の解決策を見つけることができます。 PMのタイプミスについて教えてください、ありがとう。











更新：







まず、 Habréの数式を含む記事を作成する素晴らしいサービス（ https://habrahabr.ru/post/264709/ ）に感謝します 。 彼がいなかったら、この記事はなかったでしょう。 すぐにそれについて書くのを忘れたのは残念です。







第二に、多くのコメンテーターは彼らの直感に混乱しています。 定理では、これはしばしば起こります。 はい、最初に同じ長さのテキストを入力する確率は同じです。 はい、同じ長さのテキストの出現頻度は、無限のランダムテキストで同じです。 これはすべて真実ですが、これらの事実から、 最初の行が出現する前の文字数の予想が同じになるということにはなりません。 逆もまた同様です。無限テキストの行「hh」が行「hk」よりも後に表示されるという事実から、カジノは黒の後に赤に置かれるべきではありません。







2つの行「hh」と「hk」が表示されるまで、指の期待を数えましょう。 期待値は、すべてのiの合計です。つまり、 i文字の文字列を初めて入力する確率はiです。 太字のフレーズは、最初に入力した最後の文字が検索に一致することを意味し（この確率は両方の行で同じです）、2番目に、検索文字列が最初のi-2文字間で発生しません 。 この2番目の要因は、回線ごとに異なります。 行が見つからない確率は、単にこの行が含まれていないすべてのテキストの数を、この長さのすべてのテキストの数で割ったものです。







ここで重要なのは、文字列「hk」を含まない長さkの行、合計k + 1 ：「k ... kh」、「k ... kch」、「k ... kchch」、「k ... kchchch」、...、「kch ... h」および「 h ... h。」 これは、シンボル「h」の後には「h」しか存在できないためです。







文字列「hh」を含まない長さkのドレインは、はるかに大きくなります。つまり、F k + 1-数字k + 1の下のフィボナッチ数（これらは、数字1、1、2、3、5、8、13、...です。前の2つの合計）。 たとえば、 k = 2の場合、3行は「kk」、「kch」、「hk」になります。 これらの数値は非常に急速に成長するため、文字列「kk」の期待値のすべての用語は、確率が高くなるため、より大きくなります。







数回のクリックで初めてテキストを印刷する確率は、テキストの最初と途中で一度もテキストを印刷しない確率に依存することに注意してください。 この確率は、特定の行を含まない行の数に正比例しますが、テンプレートによって異なります。







繰り返しになりますが、これは私が思いついたものではなく、非常に直感的ではありませんが、これはよく知られた事実です。 たとえば、この記事を見てください（アリスとボブに関するタスクを探してください -4段落）： https : //habrahabr.ru/post/279337/







More articles:


All Articles