
この記事では、回転軸がバレルの軸と交差しない場合の簡単な銃誘導アルゴリズムについて説明しています。 すぐに完成したものが機能しなかったことを見つける-私は学校の時間を覚えておく必要がありました。 まあ、私は覚えていたので-他の人と共有しないことは罪です。 そしてどこかで誰かが時間を節約して、それを使って他の便利な何かを作成します...
上記の計算の結果は、アーケードゲームで使用されます。 1か月間にミスはありませんでした。 シミュレーターを開発している場合、より洗練されたものが必要になる可能性があります。
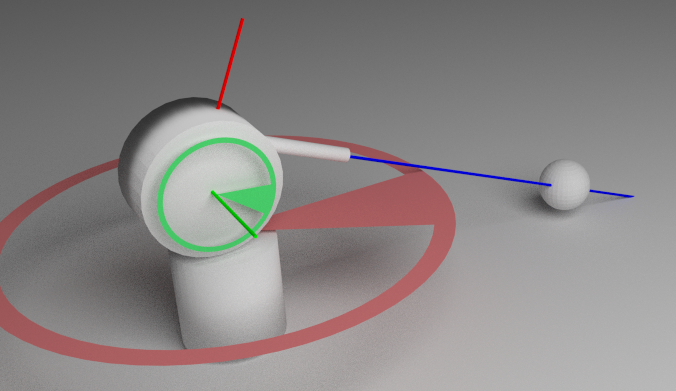
銃が与えられます。 ホバリング時、タレットは水平面(図の赤い回転軸)と垂直面(緑の軸)で回転できます。
銃モデルのプロパティ
1.バレルの軸(青で表示)は、回転軸と交差しません。
2.バレルの軸は軸Xと平行です
3.ショットの方向は正の方向Xと一致します
4.水平回転軸(赤)がZ軸に平行であるか、軸が一致しています
5.垂直回転軸(緑)がY軸に平行であるか、軸が一致しています
6.モデルの上部は、Z軸の正の方向に対応します。
ターゲットをうまく狙うには、水平と垂直の2つの回転角度を計算する必要があります
与えられたモデルの制約により(回転軸は平行であるか、対応する座標軸と一致します)、3次元空間で誘導角を見つける問題は2次元で2つに分割できます。
1.水平回転の角度は、XY平面(Z = 0)へのモデルの投影を使用して見つけることができます。
2.垂直回転の角度はXZ軸です(Y = 0)
両方のサブタスクは等しく解決されます。
開始するには、開始位置を検討します
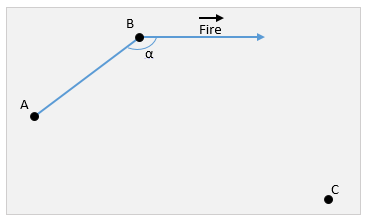
Aは回転の中心です。 垂直軸に回転軸を投影した結果。
B-発射物発射ポイント。
Fire-ショットの方向ベクトルの投影。
C-目標位置
ショットベクトルとABの間の角度を定義する

以下、角括弧はベクトルのスカラー積を示します。
ガイダンスが完了したとします。 ターゲットをオンにすると、ポイントBがDに変わり、FireベクトルがFire1になりました
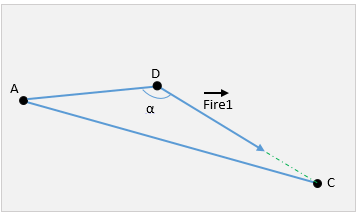
ここから、コサイン定理を使用してセグメントDCの長さを見つけることができます。
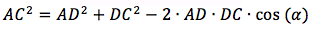
どこで


二次方程式の一般形式と一致するように式を書き直します

不明なDC
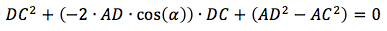
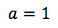

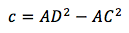
それから
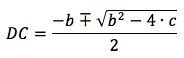
結果の2つのDC値のうち、正の値が適切です。
DCが負であることが判明した場合、ターゲットは位置誘導のために(少なくともこのアルゴリズムを使用して)アクセスできません。
次に、ポインティング前後のシステムの位置を示す図を考えます
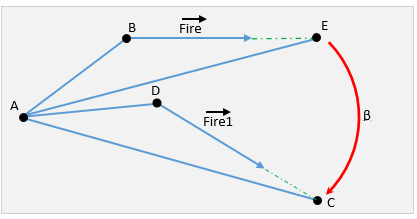
赤は、目的のポインティング角度を示します。
点Eの座標を定義します。これは、ターゲットCの座標であり、中心Aを基準として反対方向に照準の角度だけ回転します。 つまり、銃が正しい距離で発射された場合、銃はどこに行くのか、回すのを忘れます。 これを行うには、ポイントBをFireベクトルの方向に距離DCだけ移動します。

次に、照準角はベクトルAEとACの間の角度であり、スカラー積で求められます

角度は見つかりましたが、照準点はショットの方向の「上」を含むどこにでもあることを覚えておく必要があります。 つまり 別の回転方向を見つける必要があります。
ベクトルAEおよびACの方向を定義します。 これには2つのベクトルでは不十分です。 最初の2つに垂直な3番目のベクトルが必要です。 これをVと呼びます。ベクトルAEとACを持つ平面のどちら側にあるかに応じて、時計回りまたは反時計回りの回転を見る観測者の位置を決定するのは、まさにその方向です。 座標平面への投影で作業するため、目的のベクトルは3番目の座標軸に平行になります。
明確にするために、XY軸への投影の例を考えてみましょう。 この場合、垂直ベクトルの座標は(0、0、z)になります。zはゼロに等しくありません。 z記号で決定する必要があります。 投影を作成するとき、私はZ軸に沿って正の側にいるという事実から進んだため、z> 0
ベクトルの方向は、座標で構成される行列式の符号によって決まります。 最初の行は回転したベクトルの座標、2番目は1番目と3番目が回転するベクトル、ベクトルVです。この場合(AEはACと一致するように回転します)、これは

zは厳密に正になると判断したため、その符号は結果の符号に影響しません。
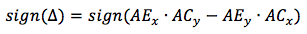
つまり、XY軸への投影の場合の最終的な回転角度は、
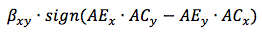
同様に、XZ軸への投影について回転方向が計算されます
さて、最後のポイント。 回転角度は、互いに完全に独立して計算することはできません。 タワーは水平軸を中心に完全な回転(-180〜180度)を行うことができますが、垂直の周りは通常不可能です(大砲がベースから外れて裏返しになっているように見えます。垂直回転を-90〜90度の範囲に制限するのは論理的です。
これを実装する最も簡単な方法。
1.水平回転の角度を見つける
2.水平回転軸を中心に反対方向にこの角度でターゲットを回転します
3.ターゲットの新しい座標の垂直ポインティング角度を計算します。
または(基本的に同じことです)最初にタワーを水平に回転させてから、垂直回転の角度を計算できます。
今、銃がヒットします。