問題の声明
「生の」迷路で作業するのはかなり不便です（少なくともグラフの導入は愛されます）。それをパーティションで接続された「部屋」に分割します。 おおよそ右の図に示すとおり。
タスクはこの形式を取りました。多くの部屋があり、それらの間で移動できます。 部屋Aから部屋Bへの道を見つける必要があります。
グラフ理論では、「部屋」は頂点と呼ばれ、それらの間の「遷移」はエッジと呼ばれます。 ルームAは開始ピーク、ルームBは終了ピークです。
右側の図のグラフは、グラフ理論でより一般的な形式で再描画できます。
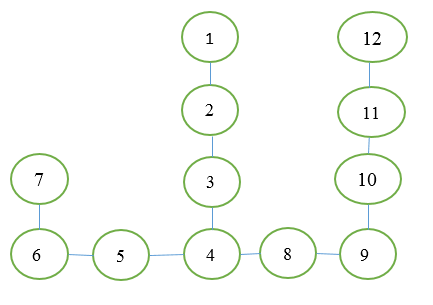
ここで、楕円は頂点（または部屋）、線はエッジ（またはそれらの間の遷移）です。 頂点1が最初で、頂点12が最後です。
そして、この問題をどのように解決しますか？
私が最初にやりたいことは、徹底的な検索を書くことです。各瞬間にピークに達し、そこからすべての隣人に行きます。
ブルートフォース
グラフは、ベクトル<vector <int >> edges配列に格納され、edges [v]にはvからのエッジがあるすべての頂点の数が格納されていると想定されています。 また、最終的な頂点番号はグローバル変数finishに保存されると想定されています。
void travel(int v) { if (v == finish) // , { cout << "Hooray! The path was found!\n"; return; } for (int i = 0; i < (int)edges[v].size(); ++i) // { travel(edges[v][i]); // } }
残念ながら、このコードは3つの頂点のグラフでは動作しません。各頂点はエッジで接続されています。頂点1から開始すると、頂点2から頂点1に移動し、再び頂点2に移動します。ある時点で、プログラムはスタックオーバーフローのために単にクラッシュします。
どうする？
すぐに思い浮かぶ解決策は、入り口の各頂点をマークし、既にマークされた頂点には決して行かないことです-これは深さのウォークです：
DFS
void DFS(int v) { if (mark[v] != 0) // , { return; } mark[v] = 1; // , if (v == finish) // , { cout << "Hooray! The path was found!\n"; return; } for (int i = 0; i < (int)edges[v].size(); ++i) // { DFS(edges[v][i]); // } }
それで何？
はい、プログラムは何らかの形で行きましたが、どのように決定するのですか？
以前の特別な配列でどの頂点から来たかを記憶します。
DFS
void DFS(int v, int from) { if (mark[v] != 0) // , { return; } mark[v] = 1; // , prior[v] = from; // , if (v == finish) // , { cout << "Hooray! The path was found!\n"; return; } for (int i = 0; i < (int)edges[v].size(); ++i) // { DFS(edges[v][i], v); // } }
その後、パスを復元するタスクは簡単になります。
get_path
vector<int> get_path() { vector<int> ans; for (int v = finish; v != start; v = prior[v]) // { ans.push_back(v); // } ans.push_back(start); reverse(ans.begin(), ans.end()); // return ans; }
なぜ機能するのですか？
アルゴリズムは、存在する場合、常にトップへのパスを見つけます。 証明：
任意のグラフGの場合：
ベース。 アルゴリズムは、1つ以下の頂点からのパスを正しく検出します（最初の頂点からそれまでのパスは同じです）。
仮定：アルゴリズムは、最初のピークからk-1以下の距離にあるすべてのピークを訪問します。
ステップ：最初の頂点から距離kにある頂点vを考えます。 明らかに、最初の頂点から距離k-1にある頂点にエッジで接続されています。これをwと呼びましょう。 したがって、頂点wを表示するときに頂点vに移動します。
アルゴリズムにはいくつのリソースが必要ですか？
アルゴリズムは各エッジを1回スキャンし、各頂点に対して一定数のアクションを実行します。 頂点の数をV、エッジをEとして表すと、操作時間はO（V + E）になります。
再帰の深さは、DFS関数の呼び出しの総数（頂点の数）を超えません。 つまり、アルゴリズムが機能するために必要なメモリの量はO（V）です。
非再帰的なDFS
再帰アルゴリズムは、非再帰形式で書き換えることができます。 DFSのコードは次のとおりです。
DFS
void DFS() { stack<int> s; s.push(start); while (!s.empty()) { int v = s.top(); s.pop(); for (int i = 0; i < edges[v].size(); ++i) { if (mark[edges[v][i]] == 0) { s.push(edges[v][i]); mark[edges[v][i]] = 1; } } } }
次は？
有益だったことを願っています。 次の記事では、DFSを使用して解決できるタスクと、BFS、ダイクストラ、その他のグラフアルゴリズムが必要な理由について詳しく説明します。