MatLabでの最適化の最適化：ネストされた匿名関数

こんにちは

私は制御システムの研究を行っており、Matlabが私の主な作業ツールです。 MatLabの可能性の1つは、数値の最適化です。 入力として変数パラメーターのベクトルを取り、最小化された基準の値を返す関数を最適化（最小化）できます。 当然、最適化のプロセスでは、目的関数が何度も呼び出され、その速度が不可欠です。 Matlabには、コードの可読性とメンテナンスの容易さを維持しながら、多くの場合パフォーマンスを大幅に改善できる優れたソフトウェアツールがあります。 タスクの例を挙げて、匿名関数とネストされた関数が何であるかを示し、次にこれら2つのツールを組み合わせてパフォーマンスを大幅に向上させる方法を示します。

問題の記述と最適化

最適化の例について長い間考えていましたが、運動学的に冗長なマニピュレーターの最適な軌道を見つけ、実験データを近似し、パラメーターを特定する、現実的なものを選択しようとしました。 しかし、このすべてがどういうわけか本質から遠ざかったので、私は非実用的ではあるが、実例となる例にこだわることにしました。 したがって、パラメーターaとbが与えられます。 範囲[0; 1]でxを見つけて、基準を最大化する必要があります。



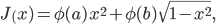
どこで 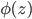-明示的にxに依存しないが、基準を計算するために必要な関数。 シードをzに設定したときに取得した最初の100万個の擬似乱数の合計のモジュールとします。 基準の値を計算するmatlab関数を作成します。

function J = GetJ(a,b,x) randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); J=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最大値を見つけたいので、最適化は最小値を探しているため、マイナス記号で値を返すことに注意してください。

ここで、 aとbの特定の値に対して最適化するには、匿名関数を作成する必要があります。 これは次のように行われます。

 a=121233; b=31235; fhnd_GetJ = @(x) GetJ(a,b,x);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、変数fhnd_GetJ



は、1つのパラメーターを取る匿名関数へのハンドルが含まれ、この匿名関数の作成時に指定されたaおよびbの値に対してGetJ(a,b, )



を計算できます。 最小化に直接進むことができます。 100万分の1の精度でxの最適値を見つけたいとしましょう：

 opt=optimset('TolX',1e-6); optimal_x=fminbnd(fhnd_GetJ,0,1,opt);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

関数fminbnd(fun,x_min,x_max)



は、区間[ x_min ;上のスカラー引数のスカラー関数を最小化します。 x_max ]。 ここでfun



は、最適化される関数のハンドルです。 最適化を実行すると、 GetJ



関数GetJ



12回呼び出されます。これは、オプションの'Display'



パラメーターを'iter'



設定することで確認できます。すべての反復が表示されます。 私のコンピューターでは、最適化に平均10ミリ秒かかります。

パフォーマンスの向上

これを最適化する方法を見てみましょう。 明らかに、 GetJ



関数を呼び出すたびに、値phi_a



およびphi_b



を完全に考慮します。これらは、 xの変化に応じて変化せず、与えられたaおよびbの値のみに依存するためです。 ここでどのように保存できますか？ 私が遭遇する最も一般的なオプションは、目的関数から予備計算を行うことです。 そのような機能を作る

 function J = GetJ2(phi_a,phi_b,x) J=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

コードは次のとおりです。

 randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); fhnd_GetJ2 = @(x) GetJ2(phi_a,phi_b,x); optimal_x=fminbnd(fhnd_GetJ2,0,1,opt);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

もちろん、これははるかに速くカウントします。 最適化は、平均で0.8ミリ秒で行われます。 しかし、この代償はコードの劣化です。 関数の整合性がphi_a



ていますphi_a



とphi_b



計算には独立した値がなく、計算とはphi_a



、 Jは必要ありません。 最適化のためだけでなく、J（a、b、x）を再度考慮する必要がある場合は、 GetJ



呼び出す代わりに、 phi_a



とphi_b



計算をドラッグするか、最適化のための関数を個別に作成する必要があります。計算用に個別に。 まあ、あまり美しくない。

matlabがこの状況を回避できるのは良いことです。 これを行うには、 GetJ



関数内にネストされた関数を作成しましょう。

 function J = GetJ3(a,b,x) randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); J=nf_GetJ(x); function out_val = nf_GetJ(x) out_val=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ネストされた関数nf_GetJ



は、親関数のスコープ内のすべての変数を参照し、原則として、それが何をどのように行うかが明確です。 これまでのところ、パフォーマンスの向上はありませんでした-最適化のための10ミリ秒すべて。



そして今、最も興味深いのは、Matlabが匿名の入れ子関数で動作できることです。 GetJ



関数は、特定の値の代わりに、独自のネストされた関数へのハンドルを返すことができます。 そして、このハンドルで関数が呼び出されると、親関数は実行されませんが、計算されたパラメーターを持つスコープは残ります！ 私たちは書きます：

 function fhnd_J = GetJ4(a,b,x) randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); fhnd_J=@(x) nf_GetJ(x); function out_val = nf_GetJ(x) out_val=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、関数のハンドルが返された変数fhnd_J



書き込まれます。これにより、変数phi_a



およびphi_b



を計算せずに、ハンドルの作成時に計算された値を使用して、使用されたパラメーターaおよびbのJの値を計算できます。 さらに、最適化は次のようになります。

 fhnd_GetJ4=GetJ4(a,b,x); optimal_x=fminbnd(fhnd_GetJ4,0,1,opt);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、そのような最適化は0.8ミリ秒で実行されます。



結果

GetJ2



例で計算を明示的に実行したときと同じ速度になりましたが、関数の整合性とその使用の利便性は保持されました。

将来、最適化と計算の両方にこの関数を使用する場合、オプションのフラグパラメーターを1つ追加できます。 設定されていない場合、関数は値を返します。 指定した場合、ネストされた関数のハンドルが返されます。