良い一日。 クラスタリング手法の1つを開発する過程で、与えられた共分散行列に沿って平面上でガウスを視覚化する（実際には楕円を描く）必要がありました。 しかし、どういうわけか、私はすぐに、4つの数字による通常の楕円の単純な描画の背後に、いくつかの困難があるとは思いませんでした。 楕円点を計算するときに、共分散行列の固有値と固有ベクトル 、 マハラノビス距離 、 カイ二乗分布が量子化されたことがわかりました。
データとその相対位置
最初の条件から始めましょう。 したがって、2次元データの配列があります
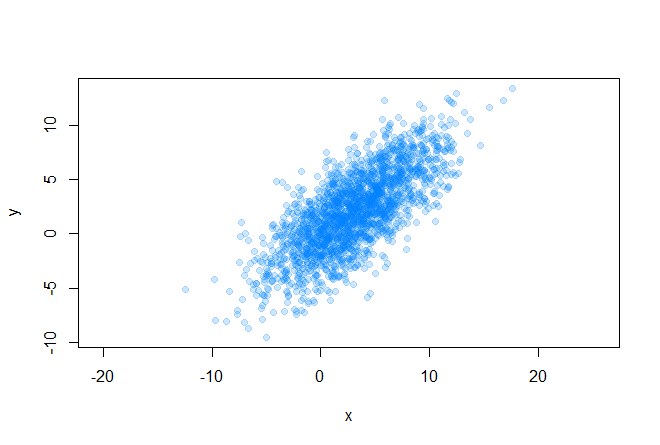
共分散行列と平均値（将来の楕円の中心）を簡単に見つけることができます：
plot(data[, 1], data[, 2], pch=19, asp=1, col=rgb(0, 0.5, 1, 0.2), xlab="x", ylab="y") sigma <- cov(data) mx <- mean(data[, 1]) my <- mean(data[, 2])
楕円の描画を開始する前に、形状のサイズを決定する必要があります。 以下に例を示します。
楕円のサイズを決定するために、共分散行列Σを持つ同じ確率分布からの2つのランダムベクトル間のマハラノビス距離を思い出します。
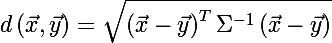
ランダムなベクトルxから、平均値μと共分散行列Σを持つセットまでの距離を決定することもできます。
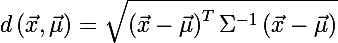
Σが単位行列に等しい場合、マハラノビス距離はユークリッド距離に縮退することに注意してください。 マハラノビス距離の意味は、変数間の相関を考慮することです。 または、言い換えると、重心に対するデータの広がりが考慮されます（広がりは楕円体の形であると想定されます）。 ユークリッド距離を使用する場合、データは重心の周りに球形に（すべての測定にわたって均等に）分布しているという仮定が使用されます。 これを次のグラフで示します。
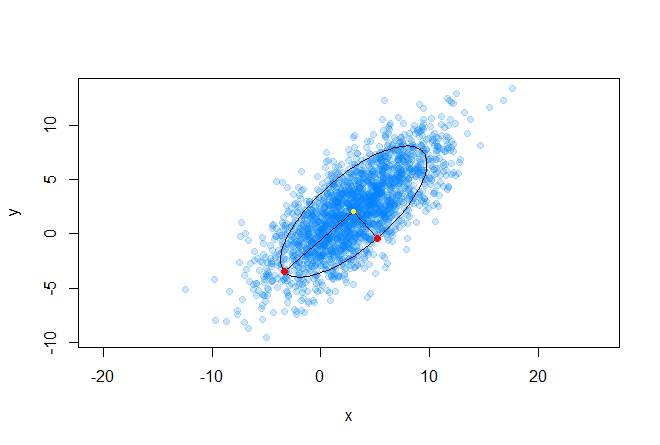
重心は黄色でマークされ、楕円の主軸にあるデータセットの2つの赤い点は、重心から同じ距離（マハラノビスの意味）にあります。
楕円とカイ二乗分布
楕円は中央の非縮退2次曲線であり、その方程式は一般的な形式で記述できます（制限を書き留めません）。
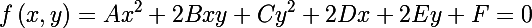
一方、楕円方程式を行列形式で（同種の2次元座標で）書くことができます：
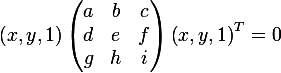
楕円が実際に行列形式で与えられていることを示すために、次の式を取得します。
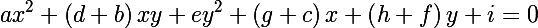
ここで、マハラノビスの距離を思い出して、その正方形を考えます：
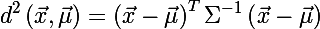
この表現は、楕円方程式を行列形式で記述するのと同じであることが簡単にわかります。 したがって、マハラノビス距離はユークリッド空間の楕円を表すと確信しました。 マハラノビス距離は、単純に、特定のポイントと質量中心との間の距離を、特定のポイントの方向の楕円体の幅で割ったものです。
理解するには微妙な瞬間がありますが、実現するのに少し時間がかかりました。マハラノビス距離の二乗は、正規分布確率変数のk番目の数の二乗の合計です 。ここで、nは空間の次元です。
このようなカイ二乗分布は、k個の独立した標準正規確率変数の二乗和の分布であることを思い出してください（この分布は自由度kの数でパラメーター化されます）。 そして、これはまさにマハラノビスの距離です。 したがって、 xが楕円の内側にある確率は、次の式で表されます。
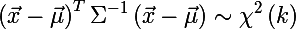
だから、楕円のサイズに関する質問の答えに来ました-カイ二乗分布の分位数によってそのサイズを決定します、これはRで簡単に行われます（qは（0、1）からで、kは自由度の数です）：
v <- qchisq(q, k)
楕円パスを取得する
必要な楕円の輪郭を生成するという考え方は非常に簡単です。単位円上のいくつかの点を取得し、この円をデータ配列の重心に移動してから、この円を目的の方向にスケーリングおよびストレッチします。 多次元ガウス分布の幾何学的な解釈を考えてみましょう：ご存じのように、これは共分散行列の固有値によって主軸の方向が与えられ、対応する固有値の根によって主軸の相対的な長さが与えられる楕円体です。
次のグラフは、対応する固有値の根にスケーリングされた共分散行列の固有ベクトルを示しています。方向は楕円の主軸に対応しています。
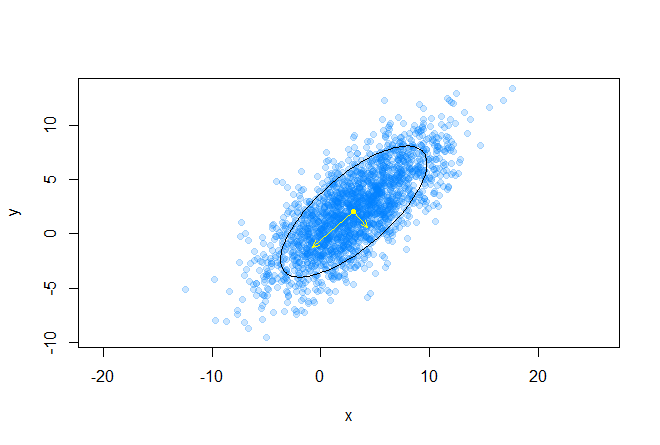
次の形式の共分散行列の展開を考えます。
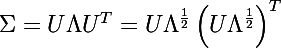
ここで、 Uは行列Σの単位固有ベクトルで形成される行列であり、 Λは対応する固有値で構成される対角行列です。
e <- eigen(sigma)
また、多次元正規分布からのランダムベクトルの次の式も考慮してください。
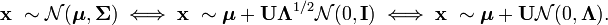
したがって、分布N（μ、Σ）は、実際には、 Λ^（1/2）でスケーリングされ、 Uで回転され、 μでシフトされた標準の多次元正規分布N（0、I）です。
次の入力を使用して、楕円を描く関数を作成しましょう。
- mx、my-重心の座標
- sigma-共分散行列
- qはカイ二乗分布の分位数です
- n-楕円のサンプリング密度（楕円が作成されるポイントの数）
GetEllipsePoints <- function(mx, my, sigma, q = 0.75, n = 100) { k <- qchisq(q, 2) # sigma <- k * sigma # e <- eigen(sigma) # angles <- seq(0, 2*pi, length.out=n) # n- cir1.points <- rbind(cos(angles), sin(angles)) # ellipse.centered <- (e$vectors %*% diag(sqrt(abs(e$values)))) %*% cir1.points # ellipse.biased <- ellipse.centered + c(mx, my) # return(ellipse.biased) # }
結果
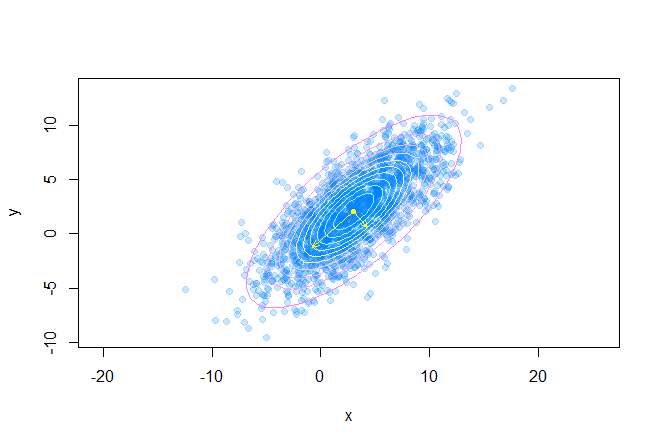
次のコードは、データセットの重心の周りに多くの信頼楕円を描画します。
points(mx, my, pch=20, col="yellow") q <- seq(0.1, 0.95, length.out=10) palette <- cm.colors(length(q)) for(i in 1:length(q)) { p <- GetEllipsePoints(mx, my, sigma, q = q[i]) points(p[1, ], p[2, ], type="l", col=palette[i]) } e <- eigen(sigma) v <- (e$vectors %*% diag(sqrt(abs(e$values)))) arrows(c(mx, mx), c(my, my), c(v[1, 1] + mx, v[1, 2] + mx), c(v[2, 1] + my, v[2, 2] + my),
その結果、次の図が得られます。
読む
コードは私のgithubにあります。