コテルニコフの定理からわかるように、アナログ信号をデジタル化して再構築するには、サンプリング周波数がアナログ信号の上限周波数の2倍以上であることが必要かつ十分です。 周期が1秒の正弦波があるとします。 次に、f = 1 ∕ T = 1ヘルツ、sin（（2 ∗π∕ T）∗ t）= sin（2 ∗π∗ t）、サンプリング周波数2ヘルツ、サンプリング周期0.5秒。 サインsin（2 ∗π∗ 0）= sin（2 ∗π∗ 0.5）= sin（2 ∗π∗ 1）= 0の式に、0.5秒の倍数である値を代入します。
どこでもゼロが取得されます。 このサインをどのように復元できますか？
インターネット検索ではこの質問に対する答えが得られませんでしたが、私が見つけることができる最大のものは、さまざまなフィルターを使用した実験へのリンクに賛否両論が投げかけられたフォーラムでのさまざまな議論でした。 コテルニコフの定理は数学的定理であり、数学的な方法によってのみ証明または反証されるべきであることが指摘されるべきです。 私がしたこと。 さまざまな教科書やモノグラフにこの定理の証明がたくさんあることが判明しましたが、多くの微妙さと詳細なしに証明が与えられたため、この矛盾がどこで発生するかを見つけることができませんでした。 また、さまざまなソースでの定理の定式化も異なっていたと思います。 したがって、最初のセクションでは、学者自身のオリジナルの仕事に続いて、この定理の詳細な証明を提供します（V.A. Kotelnikov '通信の「エーテル」とワイヤのスループットについて。通信の技術再構築と低電流産業の発展に関するI All-Union Congressの資料。1933）
元のソースにある定理を定式化します。
1秒あたり0からf1周期の周波数で構成される関数F（t）は、並べて表示できます。
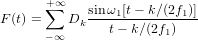
ここで、kは整数です。 ω=2πf1; DkはF（t）に依存する定数です。
証明：ディリクレ条件（有限数の最大、最小、および不連続点の有限数）を満たし、-∞から+∞の範囲で積分可能な任意の関数F（t）は、電気工学で常にそうであり、フーリエ積分で表すことができます：
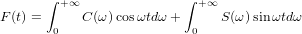
つまり 0から+∞までの周波数と、周波数に応じた振幅C（ω）dωおよびS（ω）dωの無限数の正弦波振動の合計として。 さらに
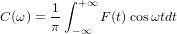
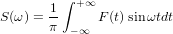
私たちの場合、F（t）が0からf1の周波数のみで構成される場合、それは明らかです。
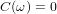
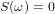
で
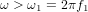
したがって、F（t）は次のように表すことができます。
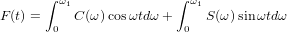
関数C（ω）およびS（ω）、セグメント上の他のものと同様
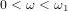
常にフーリエ級数で表すことができ、これらの級数は、期間のセクションの2倍の長さを取る場合、私たちの要求に応じて、コサインまたはサインのみで構成できます。 2ω1。
著者注：ここで説明が必要です。 コテルニコフは、C（ω）が偶数になるように関数C（ω）とS（ω）を補完する機会を利用し、S（ω）はω1に関して二重セクションの奇数関数です。 したがって、セクションの後半では、これらの関数の値はC（2 ∗ω1-ω）および-S（2 ∗ω1-ω）になります。 これらの関数は、座標ω1の垂直軸に対して反映され、関数S（ω）も符号を変更します
このように
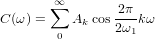
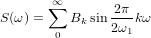
以下の表記を紹介します
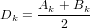
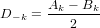
それから
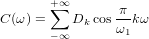
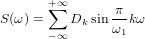
私たちが得る代わりに：
変換する
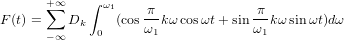
まだ変身
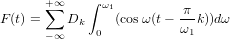
ω1を2πf1に統合して置き換えます。
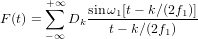コテルニコフの定理の不正確さ
証拠全体が厳密に見えます。 問題は何ですか？ これを理解するために、逆フーリエ変換のあまり広く知られていない特性に注目します。 正弦と余弦の合計から元の関数への逆変換が行われると、この関数の値は等しくなる
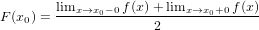
つまり、復元された関数は、制限の値の半分に等しくなります。 これは何につながりますか？ 私たちの機能が連続的であれば、それは役に立たない。 ただし、関数に有限のギャップがある場合、直接および逆フーリエ変換後の関数の値は元の値と一致しません。 ここで、間隔が2倍になる定理の証明のステップを思い出してください。 関数S（ω）は、関数-S（2 ∗ω1-ω）によって補完されます。 S（ω1）（ポイントω1の値）がゼロの場合、悪いことは何も起こりません。 ただし、S（ω1）の値がゼロでない場合、この時点で2S（ω1）に等しい不連続が発生するため、再構築された関数は元の関数と等しくなりません。
元の正弦問題に戻りましょう。 ご存じのように、サインは奇数関数であり、フーリエ変換後の画像はδ（ω-Ω0）-デルタ関数です。 つまり、この場合、サインの周波数がω1であれば、次のようになります。
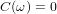
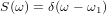
明らかに、ポイントω1で、S（ω）と-S（ω）の2つのデルタ関数をまとめてゼロを形成します。
おわりに
コテルニコフの定理は確かに素晴らしい定理です。 ただし、別の条件、つまり、
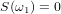
この定式化では、境界ケース、特に周波数が境界周波数ω1に等しい正弦波のケースは除外されます。これは、上記の条件でコテルニコフの定理を使用することが不可能だからです。