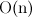 。 ここで、この事実の証拠を示します。
。 ここで、この事実の証拠を示します。
これは、Pascalの配列上にヒープを構築する手順の例です。
procedure siftdown(v:longint); var min,l,r:longint; begin l:=v*2; r:=v*2+1; min:=v; if (l <= s) and (a[l] < a[min]) then min:=l; if (r <= s) and (a[r] < a[min]) then min:=r; if min <> v then begin swap(a[min], a[v]); sift_down(min); end; end; procedure build; var i:longint; begin for i:=n downto 1 do siftdown(i); end;
だから、で構成される配列を与えましょう
 要素、および
要素、および 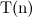 オペレーター呼び出しの数
オペレーター呼び出しの数 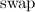 (手順で
(手順で 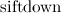 )この配列でヒープを構築するとき。 明らかに
)この配列でヒープを構築するとき。 明らかに 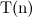 手順の操作時間を決定します
手順の操作時間を決定します  これは私たちにとって興味深いです。
これは私たちにとって興味深いです。
補題。
呼び出されたときに配列のいくつかの要素をみましょう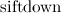 終わった
終わった 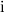 オペレーターコール
オペレーターコール 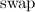 。 その後、そのインデックスは超えませんでした
。 その後、そのインデックスは超えませんでした 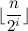 。
。
証明:
で
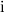 オペレーターコール
オペレーターコール 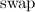 インデックス
インデックス  少なくとも要素が増加する
少なくとも要素が増加する 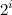 回。 さあ
回。 さあ 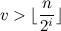 、つまり
、つまり 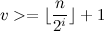 。 その後
。 その後 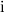 電話があります
電話があります  それは不可能です
それは不可能です  要素。
要素。 
数量を推定しましょう
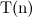 。 配列要素にインデックスを持たせる
。 配列要素にインデックスを持たせる  。 見つけるだろう
。 見つけるだろう 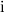 そのような
そのような 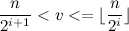 。 次に、インデックス付きの要素を配列するために
。 次に、インデックス付きの要素を配列するために  ヒープ上の所定の位置に落ちたので、これ以上は不要
ヒープ上の所定の位置に落ちたので、これ以上は不要 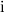 呼び出します
呼び出します 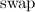 (補題による)。 そのようなインデックスを持つ要素の数は値です
(補題による)。 そのようなインデックスを持つ要素の数は値です 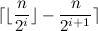 どの
どの 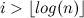 消えます。
消えます。
このように

で
 項はゼロです(したがって、手順のサイクル
項はゼロです(したがって、手順のサイクル  で始めることができます
で始めることができます 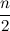 )
)
合計の各項の左因子を次のように推定します

ここから:
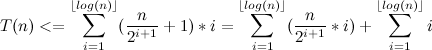
それぞれの合計を評価します。
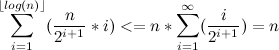
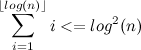
このように
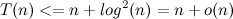 。
。
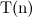 上にある関数によって制限される
上にある関数によって制限される 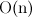 。 手段
。 手段 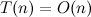 。
。
したがって、手順の操作時間
 比例する値があります
比例する値があります 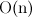 。
。