この記事は、Bootstrapメソッドに関する金曜日の記事の論理的な続きとして生まれました。 Bootstrapメソッドを守ることなく、Monte Carloメソッドに注意を払う価値があります。 ここで、実用的なタスクの1つでのモンテカルロでの経験と、このアプリケーションの正当性の理論的根拠を共有したいと思います。
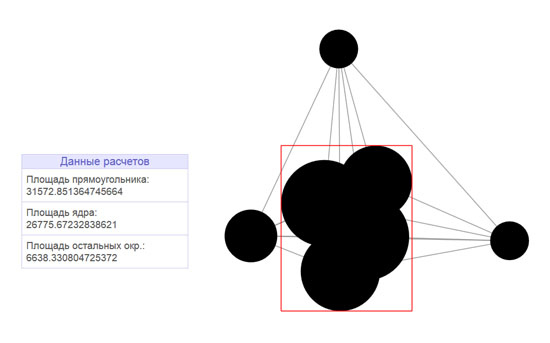
したがって、私のタスクは、図形の面積（円の交差点）を計算し、その後JavaScriptで実装することでした。 グラフの下の領域は積分です。 モンテカルロ法による統合は広く知られていますが、多くの人が正しく指摘しているように、その適用には何らかの正当化が必要です。 猫の下で詳細を尋ねます。
正当化
2つの円の交差面積を計算するタスクは、単純な幾何学的問題です（円の中心の座標とその半径がわかっています）。 2つの円の交差面積は、これらの円の対応するセグメントの面積の合計です。 さまざまな特殊なケースで、2、3、4つの円の交差領域を計算するためのソリューションがあります。
しかし、 3つの円でさえ交差する一般的な場合の解決策はそれほど簡単ではありません。 検索プロセスでは、N個の円の交差面積の計算に関する研究も見つけましたが、それらは複雑であるのと同じくらい興味深いものです。
ここで、モンテカルロ法が登場します。 現代のコンピューター設備のおかげで、この方法は、一般化された結果に基づいて、多数の統計的テストを可能にします。
したがって、モンテカルロ法を使用して図形の面積を計算するアルゴリズムは次のとおりです。
- 図は長方形に収まります。 長方形の辺の座標は既知です。つまり、その面積は既知です。
- 擬似ランダムな方法で、多数のポイントが長方形の内部に生成されます。 各ポイントについて、ポイントが元の形状内に収まったかどうかが判断されます。
- その結果、元の図形の面積は通常の割合に基づいて計算されます：図形に落ちる点の数と生成された点の総数の比率は、図形の面積とその境界矩形の面積の比率に等しくなります。
解決する必要がある最後の問題は、どういうわけか、ポイントが元の形状内に収まったかどうかを判断する必要があるということです。 私の場合、私の図は円で構成されているため、この問題は非常に簡単に解決されます。円の中心と半径は既知です。
JavaScriptタスクの実装
円の描画は、素晴らしいD3.jsライブラリを使用して行われました。 円の初期相互配置のアルゴリズムは、この記事の範囲を超えているため、最初の配置を前提とします。
円のペアの交差点の配列を収集します
var nodes = d3.selectAll("circle.node"); var squares = []; var intersections = []; nodes.each(function(node){ // var r = this.r.baseVal.value; var s = 3.14159*r*r; squares.push({node: node, square: s, r: r}); // nodes.each(function(node2){ // var center_dist = Math.sqrt(Math.pow(node.x-node2.x, 2)+(Math.pow(node.y-node2.y, 2))); var radius_sum = r + this.r.baseVal.value; if(center_dist <= radius_sum && node.index != node2.index){ // . , node.r = r; node2.r = this.r.baseVal.value; if(isNewIntersection(intersections, node, node2)) intersections.push({node1: node, node2: node2, center_dist: center_dist}); } }); });
図の面積を考慮します
var areaCalculator = { intersections: [], // , frame: {}, // circles: [], // figureArea: 0, // monteCarlo: function(p){ // var circles = []; var x1_, y1_, x2_, y2_; // var inCirclesArr = function(node){ for(var j=0; j<circles.length; j++){ if(circles[j].index==node.index){ return true; } } return false; }; for(var i=0; i<this.intersections.length; i++){ if(!inCirclesArr(this.intersections[i].node1)){ circles.push(this.intersections[i].node1); } if(!inCirclesArr(this.intersections[i].node2)){ circles.push(this.intersections[i].node2); } } this.circles = circles; circles.sort(function(a,b){ return ax-ar > bx-br ? 1 : -1; }); x1_ = circles[0].x-circles[0].r; circles.sort(function(a,b){ return a.x+ar < b.x+br ? 1 : -1; }); x2_ = circles[0].x+circles[0].r; circles.sort(function(a,b){ return ay-ar > by-br ? 1 : -1; }); y1_ = circles[0].y-circles[0].r; circles.sort(function(a,b){ return a.y+ar < b.y+br ? 1 : -1; }); y2_ = circles[0].y+circles[0].r; this.frame.x1 = x1_; this.frame.x2 = x2_; this.frame.y1 = y1_; this.frame.y2 = y2_; this.frame.area = (x2_-x1_)*(y2_-y1_); // paintRect(this.frame); // p - . 100.000, var p_positive = 0; // // p for(var i=0; i<p; i++){ var x_rand = Math.random()*(x2_-x1_)+x1_; var y_rand = Math.random()*(y2_-y1_)+y1_; var yes = false; for(var j=0; j<circles.length; j++) { if(!yes && ( (circles[j].x-circles[j].r) <= x_rand && (circles[j].x+circles[j].r) >= x_rand && (circles[j].y-circles[j].r) <= y_rand && (circles[j].y+circles[j].r) >= y_rand ) ){ yes = true; p_positive++; } } } // = *- / - this.figureArea = this.frame.area*p_positive/p; } };
ブートストラップ方式の一対の釘
Bootstrapメソッドについて具体的に説明すると、個人的な意見では、生成された情報は信頼できないため、一般的なケースで使用可能なセットに応じたデータセットのランダム生成はパターンを評価できません。 一般的に、同じように、よりインテリジェントな（そしてより厳しい）言葉でのみ、例えば、多くの著者、例えば、 経済学に関する彼の教科書の中でオルロフは言います。
おわりに
モンテカルロ法は、たとえば私の場合のように、非常に実行可能で非常に便利な場合があります。 現代のコンピューターの能力は、普通のデスクトップマシンでさえ、十分な数のテストで同様の統計的方法で動作することを可能にし、それに応じて、結果の十分な精度を得ることができます。 しかし、もちろんこれはすべて、モデルの単純化にすぎず、それ以上のことを主張することはできません。