前回の記事の最後では、ツリーに触れました。ヒープとツリーの間に共通のルートがあるため、ヒープから始めましょう。 次に、グラフに進み、ダイクストラアルゴリズムを実装します。
UPD :パフォーマンス比較を追加
ヒープは、1つのプロパティを持つ特別なツリー状の構造です。親ノードは常にその子孫以上です。 したがって、この条件下では、ヒープのルート要素は常に最大になります。 このオプションは、最大(フル)ヒープまたはmaxheapと呼ばれます。 ルート要素が最小で、各親ノードがその子孫(最小ヒープまたは最小ヒープ)以下であるヒープ。
バイナリヒープ(maxheap)は、次のように表すことができます。
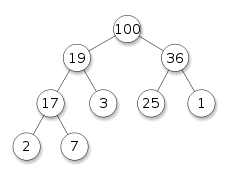
各親には2つの子があるため、バイナリです。
ヒープはバイナリツリーとして実装されますが、順序付けなどはなく、トラバースの特定の順序はありません。 ヒープはテーブル構造の変形であるため、次の基本操作が適用できます。
- create-空のヒープを作成します。
- isEmpty-ヒープが空かどうかを判断します。
- insert-ヒープに要素を追加します。
- 抽出-ヒープから要素(ルート、頂点)を抽出および削除します。
要素の取得と削除の操作は1つの抽出操作で結合されるため、最初に検討します。
ヒープからアイテムを削除するルールは、ルートアイテムのみを削除できるということです。 上記の例(100)からルート要素を削除したとします。 削除後、2つの別個のヒープが残り、何らかの方法でこれらすべてを1つの別個のヒープに再構築する必要があります。 最後のノードをルートに移動することでこれを行うのが最も簡単ですが、この場合、このようなヒープはメイン条件によっては適切ではありません。 このような束はセミヒープと呼ばれます:
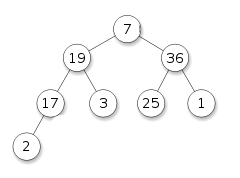
ここで、セミヒープから通常のヒープを作成する必要があります。 この問題の考えられる解決策の1つは、新しいルートを下に下げ、ルート要素をその子孫と比較し、その場所を最大の子孫で同時に変更することです。 したがって、最小の最大値を下げながら、最大の要素をルートに返します。
maxheapを配列として実装できます。 バイナリツリーのノードは2つ以上の子を持つことはできません。したがって、ノードnの数に関係なく、バイナリヒープには2n + 1個のノードがあります。
次のように束を実装します。
<?php class BinaryHeap { protected $heap; public function __construct() { $this->heap = array(); } public function isEmpty() { return empty($this->heap); } public function count() { // return count($this->heap) - 1; } public function extract() { if ($this->isEmpty()) { throw new RunTimeException(' !'); } // $root = array_shift($this->heap); if (!$this->isEmpty()) { // // $last = array_pop($this->heap); array_unshift($this->heap, $last); // $this->adjust(0); } return $root; } public function compare($item1, $item2) { if ($item1 === $item2) { return 0; } // minheap return ($item1 > $item2 ? 1 : -1); } protected function isLeaf($node) { // 2n + 1 "" return ((2 * $node) + 1) > $this->count(); } protected function adjust($root) { // if (!$this->isLeaf($root)) { $left = (2 * $root) + 1; // $right = (2 * $root) + 2; // $h = $this->heap; // if ( (isset($h[$left]) && $this->compare($h[$root], $h[$left]) < 0) || (isset($h[$right]) && $this->compare($h[$root], $h[$right]) < 0) ) { // if (isset($h[$left]) && isset($h[$right])) { $j = ($this->compare($h[$left], $h[$right]) >= 0) ? $left : $right; } else if (isset($h[$left])) { $j = $left; // } else { $j = $right; // } // list($this->heap[$root], $this->heap[$j]) = array($this->heap[$j], $this->heap[$root]); // // $j $this->adjust($j); } } } }
反対に、挿入は抽出の正反対です。要素をヒープに挿入し、可能になりメイン条件が満たされるまで要素を上げます。 完全なバイナリツリーにはn / 2 + 1ノードが含まれていることがわかっているため、単純なバイナリ検索を使用してヒープをバイパスできます。
public function insert($item) { // $this->heap[] = $item; // $place = $this->count(); $parent = floor($place / 2); // while ( $place > 0 && $this->compare( $this->heap[$place], $this->heap[$parent]) >= 0 ) { // list($this->heap[$place], $this->heap[$parent]) = array($this->heap[$parent], $this->heap[$place]); $place = $parent; $parent = floor($place / 2); } }
何が起こったかを見て、いくつかの値をヒープに挿入してみましょう。
<?php $heap = new BinaryHeap(); $heap->insert(19); $heap->insert(36); $heap->insert(54); $heap->insert(100); $heap->insert(17); $heap->insert(3); $heap->insert(25); $heap->insert(1); $heap->insert(67); $heap->insert(2); $heap->insert(7);
これらすべてを取得しようとすると、次の結果が得られます。
Array ( [0] => 100 [1] => 67 [2] => 54 [3] => 36 [4] => 19 [5] => 7 [6] => 25 [7] => 1 [8] => 17 [9] => 2 [10] => 3 )
ご覧のとおり、順序は観察されず、一般的には予想とは多少異なります。 ただし、ヒープから要素を交互に抽出する場合は、すべて問題ありません。
<?php while (!$heap->isEmpty()) { echo $heap->extract() . "n"; }
100 67 54 36 25 19 17 7 3 2 1
SplMaxHeapおよびSplMinHeap
幸いなことに、SplHeap、SplMaxHeap、SplMinHeapの既製の実装が既にあります。 必要なのは、これらを継承して比較メソッドをオーバーライドすることだけです。たとえば、次のようになります。
<?php class MyHeap extends SplMaxHeap { public function compare($item1, $item2) { return (int) $item1 - $item2; } }
このメソッドは2つのノードの比較を実行し、SplMaxHeapの場合、$ item1が$ item2より大きい場合は正の数を返し、互いに等しい場合は0、$ item2が$ item1より大きい場合は負を返します。 SplMinHeapを継承する場合、$ item1が$ item2より小さい場合、正の数を返します。
いくつかの同一の要素をヒープに配置することは推奨されません。それらの位置を決定するのが難しいからです。
SplPriorityQueue-優先度キュー
優先度キューは、キューのように動作する特別な抽象データ型ですが、ヒープとして実装されます。 SplPriorityQueueに関連して、これはmaxheapになります。 優先キューには、チケットシステムやヘルプデスクなど、かなりの数の実際のアプリケーションがあります。
SplHeapと同様に、SplPriorityQueueを継承し、比較メソッドをオーバーライドするだけです。
<?php class PriQueue extends SplPriorityQueue { public function compare($p1, $p2) { if ($p1 === $p2) return 0; // , // return ($p1 < $p2) ? 1 : -1; } }
SplPriorityQueueの主な違いは、要素の値に加えて挿入すると、この要素の優先度も予想されることです。 挿入操作では、優先順位を使用して、コンパレータが返す結果に基づいてヒープをシフトします。
優先度キューを確認し、優先度を数値として設定します。
<?php $pq = new PriQueue(); $pq->insert('A', 4); $pq->insert('B', 3); $pq->insert('C', 5); $pq->insert('D', 8); $pq->insert('E', 2); $pq->insert('F', 7); $pq->insert('G', 1); $pq->insert('H', 6); $pq->insert('I', 0); while ($pq->valid()) { print_r($pq->current()); echo "n"; $pq->next(); }
最終的に次のようになります。
I G E B A C H F D
この場合、私たちの要素は優先度の降順です-最高から最低まで(値が低いほど優先度が高くなります)。 $ p1が$ p2よりも大きい場合に正の数を返すように比較方法を変更するだけで、アイテムが返される順序を変更できます。
デフォルトでは、アイテムの値のみが取得されます。 優先度の値のみ、または値とその優先度を取得する場合は、対応する抽出フラグを設定する必要があります。
<?php // $pq->setExtractFlags(SplPriorityQueue::EXTR_PRIORITY); // ( // ) $pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);
カウント
グラフの背後には、ネットワーク最適化、ルーティング、ソーシャルネットワーク分析など、かなりの数の実際のアプリケーションがあります。 Google PageRank、Amazonからの推奨事項は、その使用例です。 記事のこのパートでは、それらが使用される2つの問題-短い道を見つける問題とストップの最小数を説明しようとします。
グラフは、キーと値のペア間の関係を表すために使用される数学的な構造です。 グラフは、一連の頂点(ノード)と、それらを接続するノード間の任意の数のリンクで構成されます。 これらの接続は、方向性(方向性)と非方向性の両方が可能です。 有向接続は2つのノード間の接続であり、A→B接続はB→Aと同じではありません。 無向接続には方向がないため、接続ABとBAは同一です。 これらのルールに基づいて、ツリーは無向グラフの1つであり、各頂点は単純な接続によってノードの1つに接続されていると言えます。
カウントにも重みを付けることができます。 重み付きグラフ、またはネットワークは、各リンク(ノードAからノードBへの遷移の「価格」)に重みを持つグラフです。 このような構造は、2つのポイント間の最適なパスまたは最も「安い」パスを決定するために広く使用されています。 GoogleMapでのパスの配置は、正確に重み付けされたグラフを使用して実行されます。
ストップの最小数(ジャンプ)
グラフ理論の一般的なアプリケーションを使用して、2つのノード間の最小ストップ数を見つけます。 木に関しては、ここでグラフは深さまたは幅の2つの方向のいずれかで木を横断するのに役立ちます。 前回、検索の詳細を調べたので、今度は別の方法を見てみましょう。
次のグラフを想像してください。
簡単にするために、このグラフは無方向であることに同意します。 タスクは、2つのノード間の最小ストップ数を見つけることです。 幅で検索するときは、ルート(ウェル、またはルートとして指定した別のノード)から開始し、レベルごとにツリーを下っていきます。 これを実現するには、まだバイパスしていないノードのリストを整理し、すべてのレベルで処理するためのキューが必要です。 一般的なアルゴリズムは次のとおりです。
- 1.キューを作成する
- 2.ルート要素をそこに追加し、訪問済みとしてマークします
- 3.キューが空になるまで:
- 3a。 現在のノードを取得する
- 3b。 現在のノードが目的のノードである場合-停止
- 3c。 そうでない場合は、未訪問の各隣接ノードをキューに追加し、訪問済みとしてマークします
しかし、グラフをバイパスせずに、どのノードが隣接しているか、または訪問されていないかをどのようにして知るのでしょうか? これは、グラフをどのようにモデル化できるかという問題につながります。
グラフ表示
通常、グラフは2つの方法で表されます-隣接ノードを記述するテーブルまたはマトリックス。
最初の例では次のようになります。
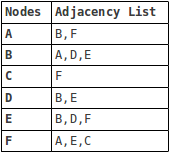
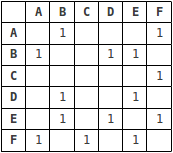
マトリックスでは、ノードの交差点で、ノードが隣接している場合、「1」が設定されます。
リストは、ほとんどの頂点が相互に接続されていない場合に便利ですが、マトリックスはより高速な検索を提供します。 最終的に、グラフの表現のタイプは、グラフで実行される操作によって異なります。 リストを使用します。
<?php $graph = array( 'A' => array('B', 'F'), 'B' => array('A', 'D', 'E'), 'C' => array('F'), 'D' => array('B', 'E'), 'E' => array('B', 'D', 'F'), 'F' => array('A', 'E', 'C'), );
そして、幅優先検索を記述します。
<?php class Graph { protected $graph; protected $visited = array(); public function __construct($graph) { $this->graph = $graph; } // () 2 public function breadthFirstSearch($origin, $destination) { // foreach ($this->graph as $vertex => $adj) { $this->visited[$vertex] = false; } // $q = new SplQueue(); // $q->enqueue($origin); $this->visited[$origin] = true; // $path = array(); $path[$origin] = new SplDoublyLinkedList(); $path[$origin]->setIteratorMode( SplDoublyLinkedList::IT_MODE_FIFO|SplDoublyLinkedList::IT_MODE_KEEP ); $path[$origin]->push($origin); $found = false; // while (!$q->isEmpty() && $q->bottom() != $destination) { $t = $q->dequeue(); if (!empty($this->graph[$t])) { // foreach ($this->graph[$t] as $vertex) { if (!$this->visited[$vertex]) { // , $q->enqueue($vertex); $this->visited[$vertex] = true; // $path[$vertex] = clone $path[$t]; $path[$vertex]->push($vertex); } } } } if (isset($path[$destination])) { echo " $origin $destination ", count($path[$destination]) - 1, " "; $sep = ''; foreach ($path[$destination] as $vertex) { echo $sep, $vertex; $sep = '->'; } echo "n"; } else { echo " $origin $destinationn"; } } }
この例を実行すると、次の結果が得られます。
もう一度カウントを見てください 
<?php $g = new Graph($graph); // D C $g->breadthFirstSearch('D', 'C'); // : // D C 3 // D->E->F->C // B F $g->breadthFirstSearch('B', 'F'); // : // B F 2 // B->A->F // A C $g->breadthFirstSearch('A', 'C'); // : // A C 2 // A->F->C // A G $g->breadthFirstSearch('A', 'G'); // : // A G
キューの代わりにスタックを使用した場合、バイパスは深くなります。
最適な方法を検索する
もう1つの一般的な問題は、2つのノード間の最適なパスを見つけることです。 前に、この問題を解決する例として、GoogleMapsでルートを構築することについて既に説明しました。 または、このタスクをルーティング、トラフィック管理などに適用できます。
この問題を解決することを目的とした有名なアルゴリズムの1つは、1959年にEdsger Weebe Dijkstraという29歳の科学者によって発明されました。 ウィキペディアでアルゴリズムの詳細を調べるか、 splitfaceのhubfaceで確認できます。 一般的に、ダイクストラのソリューションは、可能な限りすべてのノードペア間のすべての接続をチェックし、開始ノードから開始し、可能な場合はターゲットノードに到達するまで最短距離でノードのセットを更新します。
このソリューションを実装するには、いくつかの方法とその追加があります。 それらのいくつかは生産性を改善し、他のものはダイクストラのソリューションの欠点のみを指摘しました。これは、リンクに負の重みがない場合、正の重みを持つグラフでのみ機能するためです。
例として、次の正のグラフをリストに表示し、ノード間のノードの関係を示します。

<?php $graph = array( 'A' => array('B' => 3, 'D' => 3, 'F' => 6), 'B' => array('A' => 3, 'D' => 1, 'E' => 3), 'C' => array('E' => 2, 'F' => 3), 'D' => array('A' => 3, 'B' => 1, 'E' => 1, 'F' => 2), 'E' => array('B' => 3, 'C' => 2, 'D' => 1, 'F' => 5), 'F' => array('A' => 6, 'C' => 3, 'D' => 2, 'E' => 5), );
優先度キューを使用してアルゴリズムを実装し、すべての「最適化されていない」ノードのリストを作成します。
<?php class Dijkstra { protected $graph; public function __construct($graph) { $this->graph = $graph; } public function shortestPath($source, $target) { // $d = array(); // "" $pi = array(); // $Q = new SplPriorityQueue(); foreach ($this->graph as $v => $adj) { $d[$v] = INF; // $pi[$v] = null; // foreach ($adj as $w => $cost) { // $Q->insert($w, $cost); } } // - 0 $d[$source] = 0; while (!$Q->isEmpty()) { // $u = $Q->extract(); if (!empty($this->graph[$u])) { // foreach ($this->graph[$u] as $v => $cost) { // $alt = $d[$u] + $cost; // if ($alt < $d[$v]) { $d[$v] = $alt; // update minimum length to vertex $pi[$v] = $u; // } } } } // // $S = new SplStack(); // $u = $target; $dist = 0; // while (isset($pi[$u]) && $pi[$u]) { $S->push($u); $dist += $this->graph[$u][$pi[$u]]; // $u = $pi[$u]; } // , if ($S->isEmpty()) { echo " $source $targetn"; } else { // // (LIFO) $S->push($source); echo "$dist:"; $sep = ''; foreach ($S as $v) { echo $sep, $v; $sep = '->'; } echo "n"; } } }
ダイクストラのソリューションは、単純な幅優先の検索オプションであることに気付くかもしれません。 例に戻って試してみましょう。
<?php $g = new Dijkstra($graph); $g->shortestPath('D', 'C'); // 3:D->E->C $g->shortestPath('C', 'A'); // 6:C->E->D->A $g->shortestPath('B', 'F'); // 3:B->D->F $g->shortestPath('F', 'A'); // 5:F->D->A $g->shortestPath('A', 'G'); // A G
それだけです これについて、明らかに、構造に関するIgnatius Teoからの記事は終わりました。 私はそれを読んだすべての人に感謝します、多くの人々がお気に入りに最初の部分を追加することを期待していませんでしたが、お気に入りはめったに読まれず、すべての投稿が永遠にそこに残ることを私たちは知っています:)
ここからコピーされたこれらの構造の実装のパフォーマンスのベンチマーク
ご覧ください 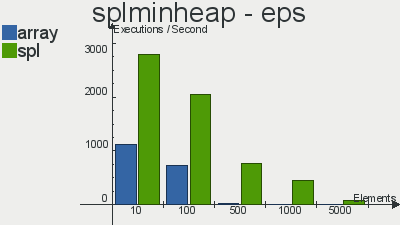
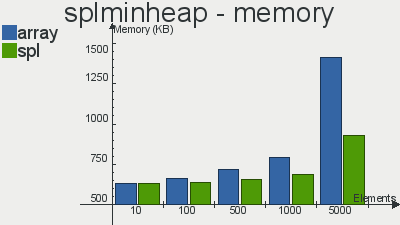

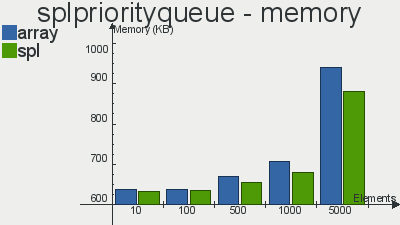




前回の記事とは異なり、ここでは、通常の配列よりもSPL実装を優先する選択が明らかです。その使用により、1秒で実行できる操作が増え、使用するメモリが少なくなります。
いつものように、PMはテキスト、翻訳、矛盾する情報、およびar慢な嘘に関する私の誤りを受け入れます。
コメントは、記事に追加する議論とそれに続く追加を歓迎します。