Clever Geek Handbook

隠れマルコフ連鎖、バウムウェルシュアルゴリズム

隠れマルコフモデル/チェーンは、データを提示するためのアプローチの一部です。 これらのアプローチがこの記事でいくつ要約されているかがとても気に入りました。



隠れマルコフモデルについて説明した前回の記事に続いて、私は自問します。良いモデルはどこで入手できますか？ 答えはかなり標準的で、良いモデルを取り、それから良いモデルを作ります。



例を挙げてみましょう。嘘発見器を実装する必要があります。嘘発見器は、人の手を振って、真実を言っているかどうかを判断します。 人が嘘をついたとき、彼の手はもう少し振ると仮定しますが、どれだけ正確かはわかりません。 モデルをランダムに取り、前の記事のビタビアルゴリズムを実行して、かなり奇妙な結果を取得しましょう。





結果のパーティションには意味がありません。 もっと正確に言えば、私が見たいものはありません。 最初の質問：選択したモデルに存在するサンプルの出現確率を評価する方法。 2番目の質問は、既存のサンプルが最も妥当なモデルを見つける方法、つまり、品質を評価する方法と新しいデータへの適応性を整理する方法です。 前後手順とバウム・ウェルチ再推定手順が答えるのは彼らです。



前後の手順により、観測値のサンプルがこのHMMモデルに現れる可能性を評価できます。 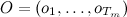O =（o_1、\ ldots、o_ {T_m}） （前の記事から取られた指定）。 評価関数を 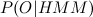P（O | HMM） 。 さらに、2つの追加機能を導入します。 



AlphaFunc<-function(S,I,T,P,O,Tm) { la<-I*Es(P,O[1]) alpha<-cbind(la) for(t in 2:Tm) { la<-as.vector((la*Es(P,O[t]))%*%T) alpha<-cbind(alpha,la) } return (alpha) } BetaFunc<-function(S,I,T,P,O,Tm) { lb<-rep(1,length(S)) beta<-cbind(lb) for(t in Tm:2) { lb<-as.vector(T%*%(Es(P,O[t])*lb)) beta<-cbind(lb, beta) } return (beta) }


機能 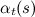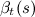\ alpha_t（s） 、 \ beta_t（s） 次の興味深いプロパティがあります。



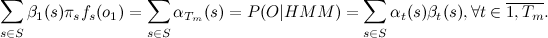
\ sum_ {s \ in S} \ beta_1（s）\ pi_s f_s（o_1）= \ sum_ {s \ in S} \ alpha_ {T_m}（s）= P（O | HMM）= \ sum_ {s \ in S} \ alpha_t（s）\ beta_t（s）、\ forall t \ in \オーバーライン{1、T_m}。

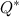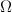そのため、HMMモデルでOサンプルの外観を評価し、隠れ状態のシーケンスを見つける方法を既に知っています。 Q ^ * 。 既存のサンプルが出現する確率が最大になるモデルを見つける方法、つまり P（O | HMM ^ *）= \ max \ limits_ {HMM \ in \ Omega} P（O | HMM） どこで \オメガ 有効なモデルのセット。 申し立てによると、最適なアルゴリズムを見つけるための正式なアルゴリズムはありませんが、モデルの変更により、少なくとも「完全性」に少し近くなる可能性があります。 これが、反復EMアルゴリズムの仕組みです。



最初のモデルがあります 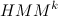うーん^ k そのようなモデルを見つける必要がある 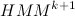HMM ^ {k + 1} あれ P（O | HMM ^ {k + 1}）\ geq P（O | HMM ^ {k}） 。 始めましょう。



さらに2つの補助関数を導入します。 



 xiGamma<-function(t,alpha,beta,S,T,P,O) { xi<-matrix(0,nrow=length(S),ncol=length(S)) denom<-alpha[,t]%*%beta[,t] for(sin in S) { for(sout in S) { nom<-alpha[sin,t]*T[sin,sout]*Es(P,O[t+1])[sout]*beta[sout,t+1] xi[sin,sout]<-nom/denom } } return(list(xi=xi,g=rowSums(xi))) } XiGammas<-function(Tm,alpha,beta,S,T,P,O) { xis<-c() gs<-c() for(t in 1:(Tm-1)) { xg<-xiGamma(t,alpha,beta,S,T,P,O) xis<-cbind(xis,as.vector(xg$xi)) gs<-cbind(gs,as.vector(xg$g)) } return(list(xi=xis,g=gs)) }


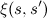\ xi（s、s '） 時間tにおける状態sから状態s 'への遷移の割合として解釈され、 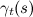\ gamma_t（s） -時間tでの状態sからの遷移の合計割合。



修正されたモデルパラメーター HMM ^ {k + 1} = \ langle M ^ {k + 1}、S ^ {k + 1}、I ^ {k + 1}、T ^ {k + 1}、E ^ {k + 1} \ラングル 次の形式になります。 



 BaumWelshFunc<-function(S,I,T,P,O,Tm) { a<-alphaLog(S,I,T,P,O,Tm) b<-betaLog(S,I,T,P,O,Tm) xg<-XiGammas(Tm, a,b, S,T,P,O) xi<-rowSums(xg$xi) dim(xi)<-c(length(S),length(S)) g<-rowSums(xi) new_I <- g/sum(g) small_t<-rep(g,length(S)) dim(small_t)<-c(length(S),length(S)) new_T <- xi/small_t norm_params<-NormalReestimation(xg$g,O[1:(Tm-1)],S) new_P<-c() for(s in S) { new_P<-c(new_P,Curry("dnorm",mean=norm_params$mu[s], sd=sqrt(norm_params$sigma2[s]))) } return(list(S=S,I=new_I,T=new_T,P=new_P,N=norm_params)) }


リセット機能 f_s（o） （この例ではNormalReestimation）は特定の状況に依存します。 アルゴリズムの古典的な実装は、観測が有限離散分布によって記述されることを前提としていますが、これは私たちには適していません。 観測値のパラメーターを推定するには、次の方法を使用することをお勧めします。 



 NormalReestimation<-function(g,O,S) { denom<-rowSums(g) mu<-g%*%O/denom sigma2<-c() for(s in S) { s2<-g[s,]%*%(O-mu[s])^2 sigma2<-c(sigma2,s2) } return(list(mu=as.vector(mu),sigma2=sigma2/denom)) }


嘘発見器の問題をより一般的な方法で検討してください。 嘘発見器が被験者の嘘と誠意にどのように反応するかの一般的なモデルがあり、時には嘘をついたり、時には真実を語る特定の個人がいます。 この特定の個人と連携するようにモデルをカスタマイズします。



与えられた：







必要です：



  1. この個人の誠実さ/嘘の場合の手の震えの分散を評価します。
  2. 彼のためにこれらの状態の変化の瞬間を決定します。




解決策：



  1. 5つを設定しましょう：



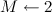    1. 状態の数 M \左矢印2 ;
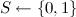    2. 州 S \左矢印\ {0,1 \} ;
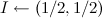    3. 初期配布 私\左矢印（1 / 2,1 / 2） ;
    4. デフォルトでは、状態が等しく、変化が平均して999クロックサイクルごとに発生するとします。

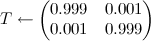      T \左矢印\左（\ begin {matrix} 0.999および0.001 \\ 0.001および0.999 \ end {matrix} \右） ;
    5. E =（N（0,1 / 2 \ cdot \ sigma ^ 2）、N（0,2 \ cdot \ sigma ^ 2）） どこで \シグマ^ 2 = var（X） 。

      それを説明します var（X） サンプル全体のサンプル分散です。 の初期評価関数 E_1、E_2 最初の状態がより低い分散値に対応し、2番目の状態が大きな分散値に対応するように選択されます。 それらが異なることは重要です。
  2. 評価関数の値が安定するまで、Baum-Welshアルゴリズムを使用してパラメーターを再構成します。
  3. ビタビアルゴリズムを使用して、各瞬間の最も可能性の高い隠れた状態を見つけます。




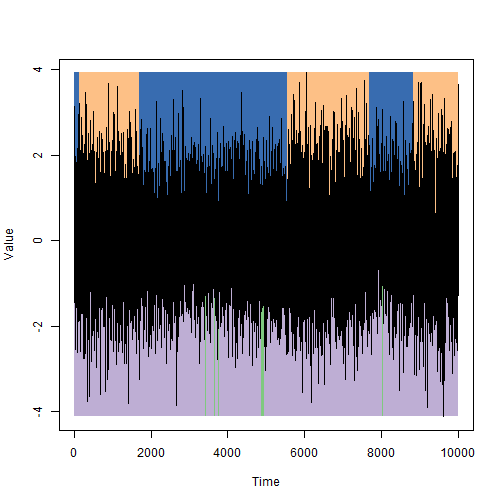
最初の図からのデータに関する答えを示します。シミュレーション中に設定された状態の上部、状態の下部、非表示マルコフ連鎖法を使用して選択された状態。





以下のグラフでは、Baum-Welshアルゴリズムの反復回数に応じた推定関数の対数の値を示しています。 緑色は、シミュレーションパラメーターに対応する評価を示します。





潜在状態を推定する際の誤差は比較的小さいですが、最初の近似が見つけたいものとあまり変わらない場合のみです。 Baum-Welshアルゴリズムは、局所的な最適値を探すための単なるステップであり、グローバルな極値に到達できないことを理解する必要があります。



数式は、 mathurl.comを使用して画像に変換されます。 いつかここで、より簡単で快適な方法で式を挿入できるようになることを望みます。ところで、 Rの構文強調表示は非常に欠けています。


More articles:


All Articles